Теоремы сложения и умножения. Условная вероятность

СЛУЧАЙНЫЕ СОБЫТИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.

ТЕОРИЯ ВЕРЯТНОСТЕЙ

Основными понятиями в теории вероятностей являются понятия события и вероятности события.

Событие – это такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может произойти или не произойти.

События будем обозначать буквами А, В, С…

Например, «Стрелок стреляет по мишени», тогда: «выстрел» – это испытание, а А={попадание} – это событие.

Все события можно подразделить на три вида: достоверное, невозможное и случайное.

Если событие неизбежно произойдет при любых условиях, то оно называется достоверным. Если событие не может произойти при любых условиях, то его называют невозможным.

Если событие при реализации некоторых условиях может произойти, а может не произойти, то оно называется случайным.

Если событие единичное, то предсказать его результат невозможно, поэтому, - предмет теории вероятностей – изучение вероятностных закономерностей массовых однородных случайных событий.

Например, нельзя определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью число выпадения герба.

Сумма (объединение) двух событий А и В – это событие С, состоящее в наступлении или А, или В (хотя бы одного из них). Обозначается С = А+В.

Произведение (совмещение) двух событий А и В – это событие С, состоящее в наступлении и А, и В (оба наступают). Обозначается С = АВ.

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Полной группой событий называется несколько попарно несовместных событий таких, что в результате испытания появится хотя бы одно из них (как правило, это всевозможные исходы испытания). Обозначается W.

Например, бросают две монеты, тогда множество W состоит из четырех событий А, В, С, D:

А = {обе выпали орлом},

В = {обе выпали решкой},

С = {первая выпала орлом, а вторая – решкой},

D = {первая выпала решкой, а вторая - орлом}.

События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Два несовместных события, образующих полную группу, называются противоположными. Обозначают А и .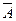

Например, подбрасывают одну монету, тогда А = {выпал орел},

а 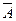= {выпала решка}.

Замечание: Событие (А +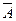) – достоверное событие, а событие (А ×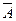) – невозможное.

Для количественной оценки появления случайного события А вводится понятие вероятности, т.е. задача вероятности – дать количественную оценку – число, характеризующее степень возможности появления события.

Каждое из возможных результатов испытания называют элементарным исходом. Те элементарные исходы, в которых интересующее нас событие наступает, называют – благоприятствующим.

Вероятностью события А называют отношение числа благоприятных для А исходов испытания к общему числу исходов. Если обозначить m – число благоприятных для А исходов, а n – число всевозможных, то

Р(А) =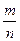

(классическое определение вероятности).

Свойства вероятности:

1⁰. Р(W) = 1.

2⁰. Вероятность невозможного события равна 0, а достоверного события равна 1. Следовательно, 0 £ Р(А) £ 1.

3⁰. Р(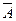) = 1 – Р(А).

Замечание. Вероятности противоположных событий удобнее обозначать буквами p и q: p=P(A), q=P()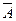

Недостатки классического определения вероятности:

1. Классическое определение предполагает конечное число испытаний. Но часто встречается бесконечное число испытаний. (В этом случае применяют, например, геометрические вероятности)

2. Не всегда результат можно представить в виде совокупности элементарных событий.

3. Трудно обосновать равновозможность событий. (Так, например, предполагают, что игральная кость имеет форму правильного куба и изготовлена из однородного материала)

Поэтому, наряду с классическим определением вероятности, используют и другие определения:

Геометрическая вероятность – это вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.д.)

Статистическая вероятность – это относительная частота или число близкое к ней.

Относительная частота события – это отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.

Теорема 1 (сложения). Если события А и В несовместны, то

Р(А+В) = Р(А) + Р(В)

Доказательство. Пусть n - общее количество испытаний; m₁ – число исходов, благоприятствующих событию А, а m₂ – число исходов, благоприятствующих событию В. По правилу суммы комбинаторики сило элементарных исходов, благоприятствующих либо А, либо В равно m₁ + m₂. Тогда Р(А+В)=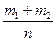=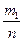+ +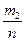=Р(А)+Р(В), ч.т.д.

Эта теорема обобщается на случай произвольного числа попарно несовместных событий: Р(А₁+А₂+…+А_n) = Р(А₁) + Р(А₂) + …+ Р(А_n).

Теорема 2. Сумма вероятностей событий А₁, А₂, …, А_n, образующих полную группу, равна 1, т.е. Р(А₁)+Р(А₂)+…+Р(А_n)=1.

Доказательство. Т.к. появление одного из событий полной группы достоверно, а вероятность достоверного события равна 1, то Р(А₁+А₂+…+А_n)=1. Любые два события полной группы несовместны, следовательно, можно применять теорему сложения: Р(А₁+А₂+…+А_n)= Р(А₁)+Р(А₂)+…+Р(А_n)=1, ч.т.д.

Событие А называется независимым от события В, если появление события А не зависит от появления события В. В противном случае события называются зависимыми.

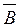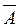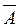Замечание. Если события А и В независимы, то независимы и события А и ; и В; и .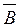

Условной вероятностью Р(В/А) называется вероятность события В, вычисленная при условии, что событие А уже произошло.

Теорема 3 (умножения). Вероятность совместного появления двух событий А и В равна

Р(АВ) = Р(А)×Р(А/В)

(причем неважно, которое из событий считать первым, а которое – вторым).

Если события А и В независимы, то теорема умножения примет вид:

Р(АВ) = Р(А)×Р(В)

Аналогично теорема умножения распространяется на случай нескольких событий:

для зависимых: Р(А₁А₂×××А_n)=Р(А₁)Р(А₂/A₁)P(A₃/A₁A₂)×××Р(А_n/A₁A₂×××A_n-1),

для независимых: Р(А₁А₂×××А_n)=Р(А₁)Р(А₂)×××Р(А_n)

Теорема 4 (вероятность появления хотя бы одного события). Пусть известны вероятности появления каждого из n независимых событий: р₁=Р(А₁), р₂=Р(А₂), …р_n=Р(А_n), тогда вероятность появления хотя бы одного из них равна

Р(А) = 1 - q₁ q₂ ×××q_n

где q _i = 1 – p _i.

Доказательство. Пусть А={произошло хотя бы одно из А₁, А₂, …, А_n}. Очевидно, 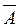==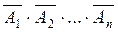{ни одно из А₁, А₂, …, А_n не произошло}. По теореме умножения для независимых событий 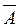Р()=Р()=.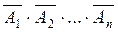

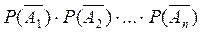Т.к. Р(А)+Р(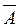)=1, то Р(А)=1-Р(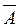)=1-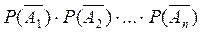=1 - q₁ q₂ ×××q_n, ч.т.д.

Частный случай. Если события А₁, А₂, …, А_n имеют одинаковую вероятность равную р, то вероятность появления хотя бы одного события равна 1-qⁿ.

Дата добавления: 2014-10-22