Определение вероятности события

1. Изложение основных теорем и формул вероятностей: теорема сложения, условная вероятность, теорема умножения, независимость событий, формула полной вероятности.

Цели: создание благоприятных условий для введения понятия вероятности события; знакомство с основными теоремами и формулами теории вероятностей; ввести формулу полной вероятности.

Ход занятия:

Случайным экспериментом (опытом) называют процесс, при котором возможны различные исходы, причем заранее нельзя предсказать, каков будет результат. Возможные исключающие друг друга исходы опыта называются его элементарными событиями. Множество элементарных событий обозначим через W.

Случайным событием называется событие, о котором нельзя заранее сказать, произойдет оно в результате опыта или нет. Каждому случайному событию А, происшедшему в результате опыта, можно поставить в соответствие группу элементарных событий из W. Элементарные события, входящие в состав этой группы, называют благоприятствующими появлению события А.

Множество W также можно рассматривать как случайное событие. Поскольку оно включает все элементарные события, то обязательно произойдет в результате опыта. Такое событие называют достоверным.

Если для данного события нет благоприятствующих элементарных событий из W, то и результате опыта оно произойти не может. Такое событие называют невозможным.

События называют равновозможными, если в результате испытания обеспечиваются равные возможности осуществления этих событий. Два случайных события называются противоположными, если в результате проведения опыта одно из них происходит тогда и только тогда, когда не происходит другое. Событие, противоположное событию А, обозначают .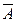

События А и В называют несовместными, если появление одного из них исключает появление другого. События А₁, А₂,..., А_n называют попарно несовместными, если любые два из них несовместны. События А₁, А₂,..., Аn образуют полную систему попарно несовместных событий, если в результате испытания обязательно произойдет одно и только одно из них.

Суммой (объединением) событий А₁, А₂,..., А_n называется такое событие С, которое состоит в том, что произошло хотя бы одно из событий А₁, А₂,..., А_n Сумма событий обозначается следующим образом:

C = A₁+A₂+…+A_n.

Произведением (пересечением) событий А₁, А₂,..., А_n называется такое событие П, которое состоит в том, что одновременно произошли все события А₁, А₂,..., А_n. Произведение событий обозначается

П =.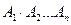

Вероятность Р(А) в теории вероятностей выступает как числовая характеристика степени возможности появления какого-либо определенного случайного события А при многократном повторении испытаний.

Допустим, при 1000 бросаний игральной кости цифра 4 выпадает 160 раз. Отношение 160/1000 = 0,16 показывает относительную частоту выпадений цифры 4 в данной серии испытаний. В более общем случае частотой случайного события А при проведении серии опытов называют отношение числа опытов, в которых произошло данное событие, к общему числу опытов:

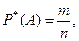
где Р*(А) - частота события А; m - число опытов, в которых произошло событие А; n - общее число опытов.

Вероятностью случайного события А называют постоянное число, около которого группируются частоты данного события по мере увеличения количества опытов (статистическое определение вероятности события). Вероятность случайного события обозначают Р(А).

Естественно, что никто и никогда не сможет проделать неограниченное число испытаний для того, чтобы определить вероятность. В этом нет и необходимости. Практически за вероятность можно принять частоту события при большом числе испытаний. Так, например, из статистических закономерностей рождения, установленных за много лет наблюдений, вероятность того события, что новорожденный будет мальчиком, оценивается в 0,515.

Если при испытании нет каких-либо причин, вследствие которых одно случайное событие появилось бы чаще других (равновозможные события), можно определить вероятность исходя из теоретических соображений. Например, выясним в случае бросания монеты частоту выпадения герба (событие А). разными экспериментаторами при нескольких тысячах испытаний было показано, что относительная частота такого события принимает значения, близкие к 0,5. учитывая, что появление герба и противоположной стороны монеты (событие В) являются событиями равновозможными, если монета симметрична, суждение Р(А)=Р(В)=0,5 можно было бы сделать и без определения частоты этих событий. На основе понятия «равновозможности» событий формулируется другое определение вероятности.

Пусть рассматриваемое событие А происходит в m случаях, которые называются благоприятствующими А, и не происходит при остальных n-m, неблагоприятствующих А.

Тогда вероятность события А равна отношению количества благоприятствующих ему элементарных событий к их общему числу (классическое определение вероятности события):

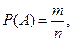
где m - количество элементарных событий, благоприятствующих событию А; n - Общее количество элементарных событий.

Рассмотрим несколько примеров:

Пример №1: В урне находится 40 шаров: 10 черных и 30 белых. Найти вероятность того, что наугад выбранный шар будет черным.

Число благоприятствующих случаев равно числу черных шаров в урне: m = 10. общее число равновозможных событий (вынимание одного шара) равна полному числу шаров в урне: n = 40. Эти события несовместны, так как вынимается один и только один шар. Р(А) = 10/40 = 0,25

Пример №2: найти вероятность выпадения четного числа при бросании игральной кости.

При бросании кости реализуется шесть равновозможных несовместных событий: появление одной цифры:1,2,3,4,5 или 6, т.е. n = 6. благоприятствующими случаями являются выпадение одной из цифр 2,4 или 6: m = 3. искомая вероятность Р(А) = m/N = 3/6 = ½.

Как видим из определения вероятности события, для всех событий

0 < Р(А) < 1.

Очевидно, что вероятность достоверного события равна 1, вероятность невозможного события равна 0.

Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей.

Для двух несовместных событий А и В вероятностей этих событий равна сумме их вероятностей:

Р(А или В)=Р(А) + Р(В).

Пример №3: найти вероятность выпадения 1 ил 6 при бросании игральной кости.

Событие А (выпадение 1) и В(выпадение 6) являются равновозможными: Р(А) = Р(В) = 1/6, поэтому Р(А или В) = 1/6 + 1/6 = 1/3

Сложение вероятностей справедливо не только для двух, но и для любого числа несовместных событий.

Пример №4: в урне находится 50 шаров: 10 белых, 20 черных, 5 красных и 15 синих. Найти вероятность появления белого, или черного, или красного шара при однократной операции изъятия шара из урны.

Вероятность вынимания белого шара (событие А) равна Р(А) = 10/50 = 1/5, черного шара (событие В) равна Р(В) = 20/50 = 2/5 и красного шара (событие С) равно Р(С) = 5/50 = 1/10. Отсюда по формуле сложения вероятностей получим Р(А или В или С) = Р(А) +Р(В) =Р(С) = 1/5 + 2/5 + 1/10 = 7/10

Сумма вероятностей двух противоположных событий, как следует из теоремы сложения вероятностей, равна единице:

Р(А) + Р( 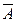) = 1

В выше рассмотренном примере вынимание белого, черного и красного шара будет событием А₁, Р(А₁) = 7/10. Противоположным событием 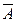₁ является доставание синего шара. Так как синих шаров 15, а общее количество шаров 50, то получаем Р(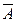₁) = 15/50 = 3/10 и Р(А) + Р(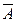) = 7/10 +3/10 = 1.

Если события А₁, А₂,..., А_n образуют полную систему попарно несовместных событий, то сумма их вероятностей равна 1.

В общем случае вероятность суммы двух событий А и В вычисляется как

Р(А+В) = Р(А) + Р(В) - Р (АВ).

Теорема умножения вероятностей:

События А и В называются независимыми, если вероятность появления события А не зависит от того, произошло событие В или нет, и наоборот, вероятность появления события В не зависит от того, произошло событие А или нет.

Вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий Р(А и В)=Р(А)·Р(В).

Пример: В одной урне 5 черных и 10 белых шаров, в другой 3 черных и 17 белых. Найти вероятность того, что при первом вынимании шаров из каждой урны оба шара окажутся черными.

Решение: вероятность вытаскивания черного шара из первой урны (событие А) – Р(А) = 5/15 = 1/3, черного шара из второй урны (событие В) – Р(В) = 3/20

Р(А и В)=Р(А)·Р(В) = (1/3)(3/20) = 3/60 = 1/20.

На практике нередко вероятность события В зависит оттого, произошло некоторое другое событие А или нет. В этом случае говорят об условной вероятности, т.е. вероятности события В при условии, что событие А произошло. Условную вероятность обозначают P(B/A).

Дата добавления: 2014-10-22