Задачи, приводящие к уравнениям эллиптического типа

УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА

Рассмотрим движение несжимаемой жидкости. Пусть некий произвольный фиксированный объем V жидкости, ограниченный поверхностью S, и массой т движется со скоростью 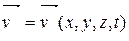. Масса т связана с плотностью 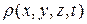соотношением

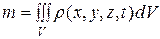. (147)

Эта масса может изменяться за счет потока жидкости через поверхность S, причем

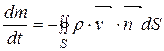, (148)

где 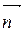- внешняя нормаль к S. Тогда из уравнений (147) и (148) получаем

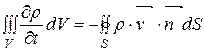. (149)

Преобразуя поверхностный интеграл, находящийся в правой части выражения (149) по формуле Остроградского (), запишем формулу (149) в виде

.

Отсюда в силу произвольности выделенного объема V следует

.

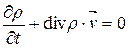Это уравнение называют уравнением неразрывности сплошной среды. Для несжимаемой жидкости плотность , и из уравнения неразрывности следует, что

. (150)

Рассмотрим установившееся течение несжимаемой жидкости, для которого 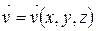. Если это течение безвихревое, то существует потенциал скоростей 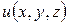, такой, что

. (151)

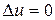или

, или 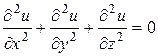, (152)

т.е. потенциал скоростей 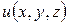удовлетворяет уравнению (152), которое является уравнением эллиптического типа и называется уравнением Лапласа.

Запишем теорему Гаусса для электростатического поля напряженностью в вакууме

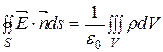. (153)

где 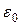- электрическая постоянная в системе Си; 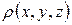- объемная плотность электрических зарядов; V – некоторый объем пространства, ограниченный замкнутой поверхностью S. С помощью теоремы Остроградского соотношение (153) можно преобразовать к дифференциальной форме

. (154)

Поскольку напряженность поля связана с потенциалом этого поля 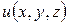соотношением

,

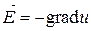то из (154) получим уравнение для потенциала электростатического поля

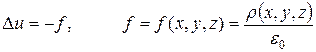, (155)

которое будет являться уравнением эллиптического типа и называться уравнением Пуассона.

Как и уравнение Лапласа, так и уравнение Пуассона являются стационарными уравнениями, т.к. искомая функция 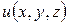не зависит от времени.

Уравнение Лапласа можно записать не только в системе декартовых координат (152), но и цилиндрической системе

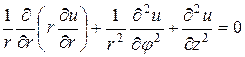(156)

и сферической системе координат

. (157)

С уравнением Лапласа связано понятие гармонической функции. Функцию называют гармонической в некоторой области D, если в этой области она непрерывна вместе со своими частными производными до второго порядка включительно и удовлетворяет уравнению Лапласа. Так, если функция зависит только от расстояния 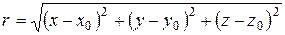точки до начала координат, то функция будет гармонической функцией везде в области D за исключением точки и будет называться фундаментальным решением уравнения Лапласа в пространстве. Функция 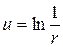будет называться фундаментальным решением уравнения Лапласа на плоскости.

Дата добавления: 2014-10-22