Дивергенция вектора в декартовой системе координат

Дивергенция вектора есть поток вектора из единицы объема истоков поля в точке.

Предварительно вычислим поток вектора сквозь замкнутую поверхность параллелепипеда. (Рис.3)

Рис.3

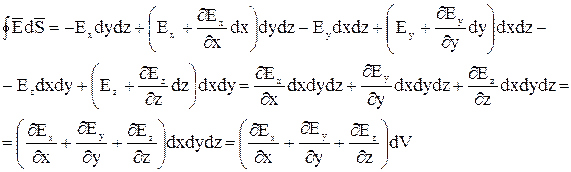
Выражает аналитическую связь дивергенции вектора с декартовой системой координат.

Ротор. Ротор-это векторная характеристика.

Ротор векторного поля 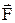называется вектор, проекция которого на положительную нормаль площади S равна пределу отношения циркуляции вектора 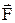к площади поверхности S, ограниченной контуром L,при стягивании контура в точку.

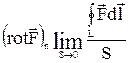
Ротор характеризует способность поля к образованию вихрей. Если в какой-то точке поля 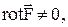то в этой точке находится вихрь (ротор соответствует плотности вихрей поля) или замкнутая силовая линия.

В декартовой системе координат вычисляется по формуле:

.

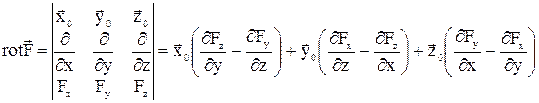Теорема Остроградского. Установим важное имеющее большое значение в теории поля равенство, выражающее собой теорему Остроградского. Это равенство имеет чисто геометрический смысл и справедливо для произвольного вектора , но мы получим его сначала на основании имеющихся в нашем распоряжении уравнений для векторов напряженности электрического и магнитного полей, а затем распространим и на произвольный вектор .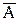

Пусть заряд q распределен в объеме V, ограниченном поверхностью S. Тогда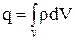. Использую теорему Гаусса в интегральной форме, можем написать: 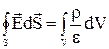. Заменяя 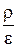через согласно той же теореме в дифференциальной форме, получим равенство:

.

Это равенство может быть написано для любого вектора , непрерывного вместе со своими первыми производными в области V и на поверхности S:

.

Оно является формулировкой теоремы Остроградского и имеет чисто геометрический смысл преобразования объемного интеграла в поверхностный.

Теорема Стокса. Установим теперь второе важное равенство. Оно также имеет чисто геометрический смысл и справедливо для произвольного вектора .

Пусть сквозь некоторую незамкнутую поверхность , ограниченную

Имеем:

.

Согласно первому уравнению Максвелла в интегральной форме, можем написать:

.

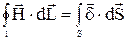Использую тоже уравнение в дифференциальной форме, заменим на . Получим:

.

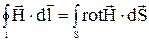Это равенство может быть написано для любого вектора, непрерывного вместе со своими первыми производными на поверхности S и на контуре l.

.

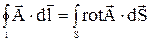Оно выражает собой теорему Стокса и имеет чисто геометрический смысл преобразования поверхностного интеграла в интеграл по контуру.

Лекция 2

Дата добавления: 2014-10-22