Тема 5. Гетероскедастичність

5.1. Виявлення гетероскедастичності та її природа

Розглянемо класичну лінійну багатофакторну модель

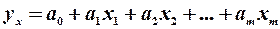(5.1)

Як завжди,

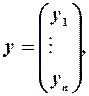
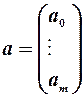, (5.2).

,

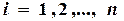
Для застосування МНК при оцінюванні параметрів моделі рані­ше було сформульо­вано основні припущення, які на практиці можуть порушуватись.

Раніше розглядався особливий випадок багатофакторного регресійного аналізу, пов'язаний з проблемою мультиколіне­арності. Тепер розгля­немо інший особливий випадок, що стосується сталості дисперсії кожної випадкової величини (гомоскедастичність залишків).

Означення 5.1. Якщо дисперсія залишків стала для кожного спо­стереження, то це явище називається гомоскедастичністю:

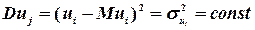, . (5.3)

Якщо це припущення не задовольняється в якомусь окремому випадку, то маємо гетероскедастичність (помилки некорельовані, але мають несталу дисперсію).

Означення 5.2. Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, то це явище називається ге- тероскедастичністю:

, . (5.4)

Розглянемо питання про доцільність припущення (5.3) і про те, що відбувається, якщо це припущення не задовольняється.

Насамперед зауважимо, що сутність припущення про гомоскедастичність полягає в тому, що варіація кожної випадкової складової навколо її математичного сподівання не залежить від значення факторів :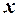

Форма гетероскедастичності залежить від знаків і значень ко­ефіцієнтів у залежності

Оскільки не спостережувана випадкова величина, ми не знає­мо справжньої форми гетероскедастичності.

У прикладних дослідженнях, як правило, використовують зручне припущення, а саме: в разі простої лінійної регресії гетероскедастичиість має форму

=

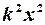
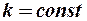(, яку потрібно оцінити).

Наслідки порушення припущення про гомоскедастичність:

1)неможливо знайти середньоквадратичне відхилення параметрів регресії, а отже, неможливо оцінити значущість пара­метрів;

2)неможливо побудувати довірчий інтервал для прогнозних значень ­ ;

3) отримані за МНК оцінки параметрів регресії не є ефективними (не мають найменшої дисперсії).

Зазначимо, що якщо, незважаючи на гетероскедастичність, ми ви­користовуватимемо звичайні процедури перевірки гіпотез, то висновки можуть бути неправильними. Зрозуміло, гетероскедастичність є суттєвою проблемою, а тому потрібно вміти з’ясовувати її наявність.

5.2. Тестування наявності гетероскедастичності

Як і в разі мультиколінеарності, єдиних правил виявлення гетероскедастичності немає, а є різноманітні тести (критерії): критерій 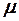, параметричний та непараметричний тести Гольдфельда–Квандта, тест Глейсера, тест рангової кореляції Спірмена та ін. Розглянемо лише деякі з них.

5.2.1. Параметричний тест Гольдфельда–Квандта

Зауваження. 1. Цей тест застосовується до великих вибірок. 2. Тест припускає нормальний розподіл і незалежність випадкових величин .

1-й крок:

спостереження (вихідні дані) впорядкувати відповідно до величи­ни елементів вектора , який може спричинити зміну дисперсії за­лишків.

2-й крок:

відкинути спостережень, які розміщені всередині векторів вихід­них даних.

3-й крок:

побудувати дві моделі на основі звичайного МНК за двома створеними сукупностями спостережень обсягом за умови, що 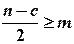, де – кількість змінних.

4-й крок:

знайти суму квадратів залишків моделей 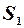і за першою і другою моде­лями:

,

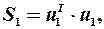
де , і 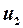– залишки відповідно за першою і другою моделями.

5-й крок:

розрахувати експериментальне значення критерію , який у разі виконання гіпотези про гомоскедастичність відповідатиме F -розподілу з 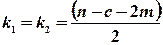ступенями свободи;

6-й крок:

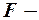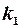значення критерію порівняти з табличним значенням критерію при вибраному рівні значущості і відповідних ступенях свободи і 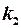; якщо , то гетероскедастичність відсутня.

Зауваження: чим більше значення , тим більша гетероскедас­тичність залишків.

5.2.2. Непараметричний тест Гольдфельда–Квандта

Цей тест базується на встановленні кількості піків значень за­лишків після впорядкування (ранжування) спостережень за . Якщо для всіх значень змінної 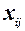залишки розподіляються приблизно од­наково, то дисперсія їх однорідна і гетероскедастичність відсутня. Якщо вона змінюється, то гетероскедастичність присутня.

Зазначимо, що цей тест не цілком надійний для перевірки на ге­тероскедастичність. Однак він дуже простий і часто використовуєть­ся для першої оцінки наявності гетероскедастичності множини спо­стережень.

5.2.3. Тест Глейсера

Перевірка на гетероскедастичність базується на побудові регресійної функції, що характеризує залежність величини залишків за мо­дулем від пояснюючої змінної 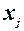,яка може зумовити зміну дисперсії залишків.

Аналітична форма регресійних функцій може мати вигляд

,

,

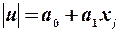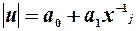тощо.

Рішення про відсутність гетероскедастичності залишків прий­мається на основі значущості коефіцієнтів 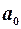і . Перевага цього ме­тоду полягає в можливості розрізняти випадок чистої () і змішаної (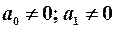) гетероскедастичності. Залежно від цього по­трібно використовувати різні матриці .

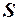Оскільки явище гетероскедастичності пов’язане з тим, що зміню­ються дисперсії залишків, а коваріація між ними відсутня, то матри­ця 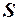у співвідношенні має бути додатно визначеною й діагональною.

Приклад. Перевірити гіпотезу про відсутність гетероскедастич­ності для побудови моделі, яка характеризує залежність заощаджень від доходів населення. Статистичні дані наведено в таблиці.

Таблиця 5.2

Дані до задачі

Рік	Заощадження	Дохід
	1,36	14,87
	1,20	14,40
	1,70	13,80
	1,84	15,60
	2,10	15,94
	1,12	16,90
	1,89	17,70
	2,30	18,67
	2,50	18,04
	1,17	19,50
	1,90	21,40
	1,95	22,70
	2,87	25,70
	2,60	27,18
	1,75	28,90
	1,96	29,45
	1,40	30,07
	2,99	30,20

Розв'язання:

Ідентифікуємо змінні: 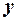– заощадження, 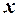– дохід. Специфікуємо модель у вигляді

Для перевірки гіпотези про відсутність гетероскедастичності за­лишків моделі застосуємо параметричний тест Гольдфельда–Квандта.

1-й крок: спостереження впорядкуємо за зростанням за величиною доходу (вектор 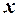), який може спричинити зміну дисперсії залишків.

Таблиця 5.3

Дані до задачі

Рік	Заощадження	Дохід
	1,70	13,80
	1,20	14,40
	1,36	14,87
	1,84	15,60
	2,10	15,94
	1,12	16,90
	1,89	17,70
	2,50	18,04
	2,30	18,67
	1,17	19,50
	1,90	21,40
	1,95	22,70
	2,87	25,70
	2,60	27,18
	1,75	28,90
	1,96	29,45
	1,40	30,07
	2,99	30,20

2-й крок: відкинемо 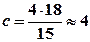спостережень усередині вектора вихідних даних.

Отримаємо дві сукупності спостережень обсягом .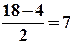

Таблиця 5.3

Перша сукупність спостережень:

	1,7	13,8
	1,2	14,4
	1,36	14,87
	1,84	15,6
	2,1	15,94
	1,12	16,9
	1,89	17,7

Друга сукупність спостережень:

	1,95	22,7
	2,87	25,7
	2,6	27,18
	1,75	28,9
	1,96	29,45
	1,4	30,07
	2,99	30,2

3-й крок: побудуємо дві моделі на основі звичайного МНК за двома ство­реними сукупностями спостережень:

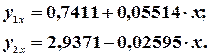
4-й крок: знайдемо суму квадратів залишків 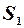і , за першою і другою мо­делями:

,

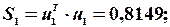
де і 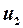– залишки відповідно за першою і другою моделями.

5-й крок: розрахуємо фактичне (експериментальне) значення критерію .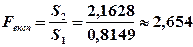

Приймаємо рівень значущості .

Число ступенів свободи: .

Розраховане значення критерію порівняємо з табличним F -критерію при рівні значущості 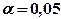і відповідних ступенях свободи :

.

Оскільки , то гетероскедастичність відсутня. Отже, МНК-оцінки параметрів регресійної моделі можуть застосовуватися для подальших досліджень.

5.3. Усунення гетероскедастичності

Розглянемо питання усунення гетероскедастичності трансформу­ванням початкової моделі. Припустимо, що за статистичними даними побудовано початко­ву регресійну модель

і на базі будь-якого тесту встановлено наявність гетероскедастичності:

Для усунення гетероскедастичності початкову модель змінюють (трансформують) так, щоб помилки мали сталу дисперсію:

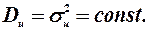
Трансформація моделі зводиться до зміни початкової форми мо­делі методом, який залежить від специфічної форми гетероскедастич­ності, тобто від форми залежності між дисперсіями залишків і зна­ченнями незалежних змінних:

(5.5).

Розглянемо сутність трансформації моделі на прикладі простої лінійної регресії.

Нехай початкова модель

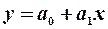(5.6),

де компоненти випадкового вектора 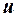гетероскедастичні, але відпові­дають іншим класичним припущенням лінійної регресії.

Припустимо, що гетероскедастичність має форму

(5.7)

де , 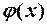–функція від .

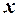Трансформація початкової моделі здійснюється діленням її на .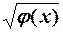

Зазначимо, що така трансформація еквівалентна застосуванню зваженого методу найменших квадратів (ЗМНК), який є особливим випадком узагальненого методу найменших квадратів (УМНК). Суть ЗМНК полягає в мінімізації зваженої суми квадратичних відхилень:

Зазначимо також, що ЗМНК, застосований до початкової моделі, дає такі самі результати, що й МНК, застосований до трансформова­ної моделі.

Твердження. Оцінки трансформованої моделі мають меншу дис­персію (ефективніші), ніж оцінки, отримані із застосуванням МНК до початкової моделі.

Нарешті, потрібно пам'ятати, що гетероскедастичність може існу­вати за рахунок неврахованих факторів (поганої специфікації моделі). У цьому разі можливим рішенням є включення неврахованих фак­торів у модель. Сліпе застосування трансформації (без аналізу при­чин гетероскедастичності) зробить гомоскедастичною випадкову змінну, однак оцінки параметрів залишаться неправильними через неврахування важливих факторів.

Дата добавления: 2014-10-23