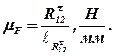Метод жорсткого важеля Жуковського

План

План

План

План

1.Принцип Даламбера. Головний вектор і головний момент сил інерції.

2.Принцип можливих переміщень.

3.Загальне рівняння динаміки (принцип Даламбера-Лагранжа).

1. Принцип Даламбера. Головний вектор і головний момент сил інерції

До цього для розв’язання задач динаміки ми користувались диференціальними рівняннями, які виходили із основного закону динаміки. Це не єдиний шлях. Можна в основу розв’язків покласти загальні положення, які називаються принципами механіки.

Розпочнемо з принципу Даламбера.

Нехай на точку масою m діє система активних сил, рівнодійну яких ми позначимо через 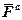, і реакція в'язі (якщо точка невільна). Під дією цих сил точка буде рухатись по відношенню до інерціальної системи відліку з деяким прискоренням .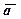

Введемо величину , яка має розмірність сили. Векторну величину, яка дорівнює за модулем добутку маси точки на її прискорення і напрямлена в бік, протилежний цьому прискоренню, називають силою інерції точки.

Тоді рух точки має таку властивість: якщо в будь-який момент часу до активних сил і реакцій в'язі, які діють на точку, приєднати силу інерції, то здобута система буде зрівноваженою, тобто:

Це положення і виражає принцип Даламберадля матеріальної точки.

Це твердження еквівалентне другому закону Ньютона для цієї точки:

.

Розглянемо механічну систему, яка складається із n точок. Нехай точка масою m_k під дією прикладених до неї зовнішніх і внутрішніх сил і (в які входять і активні сили, і реакції в’язей) рухається по відношенню до інерціальної системи з прискоренням 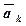. Позначивши силу інерції , дістанемо:

тобто , 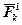і 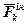утворюють зрівноважену систему сил.

Аналогічні результати будуть для всіх точок системи. Отже, принцип Даламбера для системи: якщо в будь-який момент часу до кожної із точок системи, крім зовнішніх і внутрішніх сил, що діють на неї, приєднати відповідні сили інерції, то здобута система буде зрівноваженою і до неї можна застосовувати всі рівняння статики.

Із принципу Даламбера можна дістати всі загальні теореми динаміки.

Із статики відомо, що для системи, яка перебуває у рівновазі, геометрична сума всіх сил і сума їх моментів відносно будь-якого центра дорівнюють нулю. Тоді на основі принципу Даламбера:

Введемо позначення:

Величини 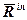і 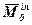– це головний вектор і головний момент відносно центра O системи сил інерції. Тоді, враховуючи, що геометрична сума внутрішніх сил і сума їх моментів дорівнює нулю, дістанемо:

, (1)

. (2)

Використання цих рівнянь спрощує розв’язок задач динаміки.

Порівнюючи рівняння (1) з рівнянням 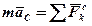(виражає теорему про рух центра мас), знайдемо, що:

тобто головний вектор сил інерції механічної системи (зокрема, твердого тіла) дорівнює добутку маси системи (тіла) на прискорення центра мас і напрямлений протилежно цьому прискоренню.

Якщо прискорення розкласти на дотичне і нормальне, то вектор розкладеться на складові:

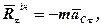
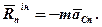
Нормальну складову сили інерції називають відцентровою силою інерції.

Порівнюючи рівняння (2) з рівнянням (виражає теорему моментів), дістанемо:

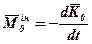і ,

тобто головний момент сил інерції механічної системи (твердого тіла) відносно деякого центра O або осі z дорівнює взятій зі знаком „ – ” похідній за часом від кінетичного моменту системи (тіла) відносно того ж центра або тієї ж осі.

У випадку плоскопаралельного руху система сил інерції тіла зводиться до рівнодійної , прикладеної в центрі мас, і пари з моментом 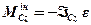(напрямок М^ін протилежний ε).

2.Принцип можливих переміщень

Можливим переміщенням механічної системи будемо називати будь-яку сукупність елементарних переміщень точок цієї системи із положення, яке вона займає в даний момент часу і які допускаються всіма в’язями, накладеними на систему.

Слід розрізняти дійсне переміщення точки, яке вона здійснює за елементарний проміжок часу dt, і можливе переміщення , яке точка не виконує, а тільки могла б виконати, не порушуючи накладених на неї в’язей.

Введемо деякі поняття.

Можливою роботою називається робота, яку точка могла б виконати на переміщенні, яке збігається з можливим переміщенням цієї точки. Можливу роботу активних сил 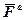позначимо 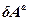(), а можливу роботу реакції в’язі – символом ().

Ідеальними називаються в’язі, для яких сума елементарних робіт їх реакцій на будь-якому можливому переміщенні системи дорівнює нулю, тобто:

Для визначення необхідної умови рівноваги доведемо, що якщо механічна система з ідеальними в’язями перебуває під дією прикладених сил у рівновазі, то при будь-якому можливому переміщенні системи повинна виконуватись рівність:

або

,

де α_k – кут між силою і можливим переміщенням.

Позначимо рівнодійну всіх (і зовнішніх, і внутрішніх) активних сил і реакцій в’язей, які діють на точку B_k, відповідно і 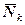. Тоді, оскільки кожна точка перебуває в рівновазі, то 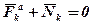, а отже, і сума їх робіт на будь-якому переміщенні точки B_k теж буде дорівнювати нулю, тобто . Склавши такі рівняння для всіх точок і додавши їх почленно, дістанемо:

Але оскільки в’язі ідеальні, а 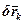є можливим переміщенням точки B_k, то друга складова за умовою дорівнює нулю. Тоді рівність виражає умову рівноваги системи.

Принцип можливих переміщень: для рівноваги механічної системи з ідеальними в’язями необхідно і достатньо, щоб сума елементарних робіт всіх активних сил, що діють на неї, на будь-якому можливому переміщенні системи дорівнювала нулю.

Подамо зазначену рівність в аналітичній формі:

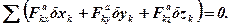
Принцип можливих переміщень встановлює загальну умову рівноваги механічної системи, яка не вимагає розгляду рівноваги окремих частин цієї системи і дозволяє при ідеальних в’язях виключити всі наперед невідомі реакції в’язей.

3.Загальне рівняння динаміки (принцип Даламбера-Лагранжа)

Принцип можливих переміщень дає загальний метод розв’язання задач статики. З іншого боку, принцип Даламбера дозволяє використовувати методи статики для розв’язання задач динаміки. Отже, застосовуючи ці два принципи одночасно, ми можемо дістати загальний метод розв’язання задач динаміки.

Розглянемо систему матеріальних точок, на яку накладені ідеальні в’язі. Якщо до всіх точок системи, крім активних сил і реакції в’язей , додати відповідні сили інерції , то згідно принципу Даламбера здобута система буде перебувати в рівновазі. Тоді, скориставшись принципом можливих переміщень, знайдемо:

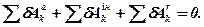
Але остання сума за умовою (ідеальні в’язі) дорівнює нулю, і остаточно маємо:

Звідси принцип Даламбера-Лангранжа: при русі механічної системи з ідеальними в’язями в кожний момент часу сума елементарних робіт всіх активних сил і всіх сил інерції на будь-якому можливому переміщенні системи буде дорівнювати нулю.

Це рівняння виражає принцип Даламбера-Лагранжа і називається загальним рівнянням динаміки.

В аналітичній формі маємо:

Ці рівняння дають змогу складати диференціальні рівняння руху механічної системи.

Питання для самоконтролю

1.Сформулювати принцип Даламбера для матеріальної точки.

2.Сформулювати принцип Даламбера для механічної системи.

3.Що називається можливим переміщенням механічної системи?

4.Дати означення можливій роботі, ідеальним в’язям.

5.Сформулювати принцип можливих переміщень.

6.Сформулювати принцип Даламбера–Лагранжа.

ДИНАМІКА МЕХАНІЗМІВ ТА МАШИН

Лекція № 34

Тема: “Вступ у динаміку механізмів”

1. Основні завдання динаміки механізмів і машин

2. Класифікація сил, що діють у машинах.

3. Зведена і зрівноважуюча сили.

4. Статична визначуваність механізмів в їх силовому аналізі.

5. Методи силового дослідження механізмів.

1. Основні завдання динаміки механізмів та машин

При розгляді питань кінематичного дослідження механізмів ми завжди виходили з того, що рух ведучих ланок заданий, а рух ведених ланок вивчався в залежності від законів руху ведучих ланок. При цьому сили, які діють на ланки механізму, і сили, які виникають у процесі руху, не враховували. Таким чином, при кінематичному аналізі дослідження руху механізмів ведеться з урахуванням тільки їх структури і геометричних співвідношень між розмірами їх ланок.

Динамічний аналіз механізмів має своїми завданнями:

а) вивчення впливу зовнішніх сил, сил ваги ланок, сил тертя та сил інерції на ланки механізму, на елементи ланок, на кінематичні пари та нерухомі опори і встановлення способів зменшення динамічних навантажень, які виникають у процесі руху механізму.

б) вивчення режиму руху механізму під дією заданих сил і встановлення способів, які забезпечують задані режими руху механізму.

Перше завдання носить назву силового аналізу механізму, а друге – динаміки механізмів. У динамічний аналіз може входити і низка інших завдань, але для їх розв’язання використовується, наприклад, теорія пружності, а в теорії механізмів і машин вважають, що всі ланки абсолютно жорсткі. Тому ці завдання розглядаються в спеціальних курсах.

2. Класифікація сил, що діють в машинах

Отже, завданням динаміки машин є вивчення руху машин з урахуванням сил, що діють у них.

У процесі роботи будь-якої машини всі сили, що діють на її ланки, можна поділити на шість груп:

1) сили корисного опору (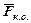) – сили опору, подолання яких необхідно для виконання заданого технологічного процесу.

2) рушійні сили () – сили, прикладені до ланок механізму, які виконують додатну роботу.

3) сили шкідливого опору () – сили опору, на подолання яких витрачається додаткова робота зверх тієї, яка необхідна для подолання корисного опору.

Сили опору (шкідливого і корисного) виконують від’ємну роботу.

Сили шкідливого опору в свою чергу поділяються на сили тертя і сили опору середовища. Перші можуть бути прикладені лише в кінематичних парах, другі – в будь-яких інших точках ланок механізму.

4) сили ваги () ланок:

G=m·g,

де m – маса ланки; g – прискорення вільного падіння.

5) сили інерції (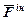) ланок, які визначаються за формулою:

де – прискорення центра мас ланки.

6) сили реакції () – сили, які виникають у кінематичних парах і є тиском ланок одна на іншу.

3. Зведена і зрівноважуюча сили

Зведеною називається сила, умовно прикладена до однієї із точок механізму, робота якої на її елементарному переміщенню дорівнює сумі робіт всіх реальних сил на їх елементарних переміщеннях.

Зазвичай зведена сила прикладається до кінця кривошипа, а напрямок її обирається перпендикулярним до нього.

Зрівноважуючою силою називається сила, яка дорівнює зведеній, але напрямлена в протилежний їй бік.

Зрівноважуюча сила зрівноважує зведену, а отже, зрівноважить і всі реальні сили, які діють на ланки механізму, оскільки вона справляє на кривошип таку ж дію, як і зведена сила.

4. Статична визначуваність механізмів в їх силовому аналізі

У процесі силового аналізу механізмів визначаються реакції у всіх кінематичних парах і зрівноважуюча сила. З’ясуємо, чи завжди завдання силового аналізу плоского механізму є статично визначуваним.

Для цього розглянемо, скільки невідомих мають реакції в різних кінематичних парах.

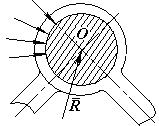
Рис.1

У обертальній кінематичній парі (рис.1) результуюча реакція проходить через центр шарніра О. Величина і напрямок цієї реакції невідомі. Відома тільки точка прикладання.

Рис.2

У поступальній парі (рис.2) реакція напрямлена перпендикулярно до осі відносного руху ланок пари. Напрямок реакції – відомий, а невідомими є величина і точка прикладання.

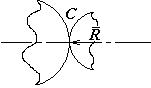
Рис.3

У вищих кінематичних парах (рис.3) точка прикладання і лінія дії реакції відомі (точкою прикладання є точка С дотикання елементів ланок, а лінія дії – нормаль), невідома лише величина.

Отже, реакції в нижчих кінематичних парах мають по два невідомі, а у вищих – одне. Запишемо умову статичної визначуваності для кінематичних ланцюгів. Оскільки для кожної ланки, яка виконує плоскопаралельний рух, можна написати три рівняння руху, то кількість рівнянь, які ми можемо скласти для n ланок, дорівнює 3n. Кількість невідомих, які треба визначити буде дорівнювати для пар 5 класу 2р₅, а для пар 4 класу – р₄.

Отже, кінематичний ланцюг буде статично визначуваним, якщо задовольняється умова:

3n = 2р₅ + р_{4 .}

Для нижчих пар маємо:

3n = 2р₅

або

3n–2р₅ = 0.

А це є рівнянням групи Ассура.

Отже, будь-яка група Ассура є статично визначуваною.

5. Методи силового дослідження механізмів

Якщо при дослідженні у перелік заданих сил не входять сили інерції ланок, то розрахунок називається статичним.

Якщо сили інерції входять у силовий розрахунок механізму, то він називається кінетостатичним.

Існують такі методи силового аналізу:

1) аналітичний (застосовується рідко із-за своєї громіздкості й складності, переважно тоді, коли кінематичне дослідження теж виконувалось аналітичним методом, щоб не втратити точність розрахунків);

2) метод планів сил (найпоширеніший, застосовується тоді, коли задано багато сил і необхідно визначити реакції в кінематичних парах; недоліком є його громіздкість);

3) метод безпосереднього розкладання сил (застосовується тоді, коли задано мало сил (одна чи дві) і необхідно визначити реакції в кінематичних парах);

4) метод жорсткого важеля Жуковського – це графічна інтерпретація методу, основаного на принципі можливих переміщень; застосовується тоді, коли необхідно визначити лише зрівноважуючу силу, а реакцій у кінематичних парах визначати не потрібно.

Питання для самоконтролю

1. Які основні завдання висуває динаміка механізмів та машин?

2. Класифікація сил, що діють у машині, їх коротка характеристика.

3. Дати означення зведеній і зрівноважуючій силам.

4. Коли завдання силового аналізу механізму є статично визначуваним?

5. Перелічити методи силового дослідження механізмів і дати їх коротку характеристику.

Лекція № 35

Тема: “Силовий аналіз плоских механізмів методом планів”

1. Послідовність силового аналізу механізму ІІ класу.

2. Визначення сил інерції ланок.

3. Визначення реакцій у кінематичних парах групи Ассура ІІ класу.

4. Особливості розрахунку групи Ассура, яка містить у собі поступальну пару.

5. Силовий аналіз кривошипа.

1. Послідовність силового аналізу механізму ІІ класу

Приступаючи до силового дослідження механізму, необхідно передусім виконати його структурний аналіз, у процесі якого, зокрема, розділити його на групи Ассура і ведучий механізм І класу. Кожна група розглядається окремо, починаючи із найвіддаленішої від кривошипа групи.

При силовому дослідженні кожної групи Ассура спочатку визначаються реакції в зовнішніх парах, а потім у внутрішній. Реакції у зовнішніх парах визначаються по частинах. Передусім знаходять дотичні (тангенціальні) складові реакцій (перпендикулярні до ланок) із суми моментів відносно середньої точки діади всіх сил, які діють на кожну із двох ланок. Потім будується план (многокутник) сил для групи Ассура за рівнянням її рівноваги, із якого визначаються нормальні складові реакцій зовнішніх пар. Повні реакції обчислюють як геометричну суму їх нормальної та дотичної складових. Щоб знайти реакції у внутрішній парі групи, будується план сил, що діють на одну ланку, за рівнянням її рівноваги.

Розглядаючи другу, третю і всі наступні діади в реакції кінематичної пари, що з’єднує структурні групи між собою, напрямок змінюється на протилежний.

В останню чергу розглядається рівновага кривошипа й будується план сил для нього.

2. Визначення сил інерції ланок

Із курсу теоретичної механіки відомо, що сили інерції елементарних мас ланки у складному плоскому русі зводяться до результуючої сили інерції:

і моменту сил інерції

,

де – прискорення центра мас; ε – кутове прискорення ланки; 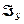– момент інерції ланки відносно осі, яка проходить через центр мас S.

Знак “мінус” у формулах показує, що сила інерції напрямлена в бік, протилежний прискоренню центра мас ланки, а момент сил інерції M^ін – протилежний кутовому прискоренню ланки.

Для спрощення розрахунків силу інерції і момент сил інерції M^ін можна замінити однією силою, яка дорівнює силі і паралельна їй, але прикладена умовно в деякій точці К. Ця точка лежить на перпендикулярі до напрямку повного прискорення і знаходиться на такій відстані h від основи перпендикуляра, що момент прикладеної в ній сили відносно центра мас S ланки дорівнює моменту M^ін:

,

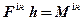звідки:

.

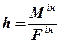Отже, для визначення і M^ін необхідно попередньо знайти прискорення і ε із плану прискорень.

Нехай маємо ланку АВ (рис.1,а), для якої побудований план прискорень (рис.1,б).

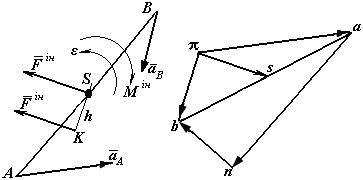
а) б)

Рис. 1

Оскільки точка S розділяє ланку АВ навпіл, то на плані прискорень відрізок аb поділимо навпіл і знайдемо точку s. Сполучивши її з полюсом, визначимо повне прискорення центра мас:

a_S=(πs)·μ_a.

Величина сили інерції визначиться як:

т(πs)·μ_a,

де m – маса ланки.

Паралельно відрізку (πs), але в протилежний бік напрямимо . Визначивши величину і напрямок кутового прискорення ε, знайдемо М^ін:

,

де – дійсна довжина ланки в метрах.

.

Зобразимо М^ін у вигляді дугової стрілки (напрямок – за ходом годинникової стрілки). Можемо замінити і М^ін на одну , прикладену в точці K на відстані .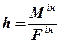

3. Визначення реакцій в кінематичних парах групи Ассура ІІ класу.

Розглянемо завдання про визначення реакцій у кінематичних парах групи Ассура ІІ класу АВС (рис.2,а).

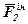При цьому відомими є величини сил ваги ланок , ; сил їх інерції , ; моменти сил інерції , 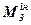. Слід визначити реакції у кінематичних парах А, В, С.

Складемо рівняння рівноваги групи Ассура. Вона перебуває у рівновазі тоді, коли сума всіх сил, які діють на неї, дорівнює нулю, тобто многокутник сил повинен бути замкнутим. Оскільки напрямки реакцій у точках А і В невідомі, то розкладаємо їх на нормальні (паралельні ланкам) та тангенціальні (перпендикулярні ланкам) складові. У позначенні реакції 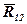перший індекс показує, з боку якої ланки діє реакція, а другий – ланку, на яку діє реакція. Маємо:

.

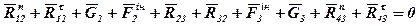Оскільки реакції у внутрішній кінематичній пар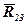і і однакові за модулем і протилежні за напрямком, то їх можна виключити з рівняння. Тоді дістанемо:

.

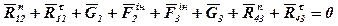З метою визначення дотичної складової реакції складемо рівняння моментів відносно точки В (середньої точки діади) всіх сил, що діють на ланку 2:

.

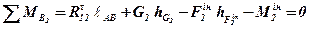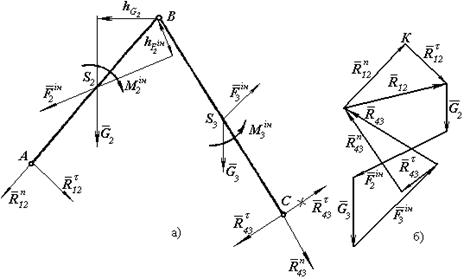
в)

Рис.2

У цьому рівнянні тільки одне невідоме – . Плечі сил вимірюються безпосередньо на схемі.

Із рівняння маємо:

.

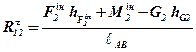Аналогічно визначаємо реакцію, склавши рівняння моментів відносно точки В всіх сил, які діють на третю ланку:

,

звідки:

.

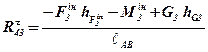Якщо дістали від’ємне значення реакції, то на схемі її напрямок закреслюють і змінюють на протилежний. Нехай зі знаком “–”.

Щоб знайти нормальні складові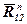та 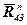, будуємо план (многокутник) сил. Для цього із довільної точки К відкладаємо відому дотичну реакцію в точці А. Масштаб побудови обчислюємо за формулою:

З кінця цього вектора в будь-якій послідовності в обраному масштабі відкладаємо решту сил, а передостанньою – . Потім через кінець цього вектора та з полюса перпендикулярно дотичним складовим проводимо прямі (напрямки нормальних реакцій 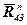та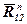), точка перетину яких визначить їх величини і замкне многокутник.

Повні реакції визначаємо як геометричні суми їх дотичних і нормальних складових:

;

.

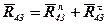Дійсні значення реакцій:

;

.

Отже, реакції у зовнішніх кінематичних парах визначені. Щоб визначити реакцію у внутрішній кінематичній парі, запишемо умову рівноваги для кожної ланки окремо:

;

.

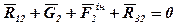У кожному рівнянні невідомо тільки по одній силі. Будуємо за цими рівняннями плани сил і визначимо невідомі сили як замикальні вектори многокутників (рис.2,в).

Як бачимо, ці реакції (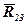i ) однакові за величиною, паралельні, але протилежні за напрямком. Отже, всі побудови виконані правильно. Побудова планів сил для обох ланок є своєрідною перевіркою правильності розв’язання задачі.

4. Особливості розрахунку групи Ассура, яка містить у собі поступальну пару

Послідовність силового аналізу такої групи Ассура нічим не відрізняється від аналізу діади з одними обертальними парами, за винятком того, що напрямок реакції 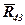буде відомий: перпендикулярний до напрямної поступальної пари (рис.3).

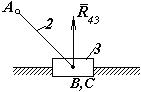
Рис.3

Цю реакцію не треба розкладати на складові, а отже, і складати рівняння моментів сил, що діють на ланку 3. Решта розрахунків виконується аналогічно двоповідковій групі Ассура.

5. Силовий аналіз кривошипа

Кривошип зазвичай зрівноважений, оскільки обертається рівномірно навколо осі. Отже, його сили інерції і ваги при силовому дослідженні не враховуються.

Складемо умову рівноваги кривошипа (рис.4,а):

.

а) б)

Рис.4

Реакція відома за величиною і напрямком (= –). Отже, в цьому рівнянні два невідомі: зрівноважуюча сила (напрямлена перпендикулярно до кривошипа) і реакція 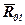(напрямлена вздовж кривошипа). Оскільки на кривошип діють три сили, то вони повинні перетинатися в одній точці відповідно до теореми про три непаралельні сили (див. лекц. №3). Дві із них прикладені до точки А, а тому і третя сила 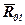повинна пройти через точку А.

За рівнянням рівноваги будуємо план сил і визначаємо величини сил F_зр та R₀₁ (рис.4,б).

Дійсні значення сил:

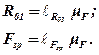
Щоб знайти ведучий момент, перемножимо величину зрівноважуючої сили на довжину кривошипа :

.

Питання для самоконтролю

1. Яка послідовність силового аналізу механізму ІІ класу?

2. Як визначити силу інерції та момент сили інерції ланки механізму?

3. Визначення дотичних та нормальних реакцій у зовнішніх кінематичних парах групи Ассура.

4. Як визначається реакція у внутрішній кінематичній парі групи Ассура?

5. Особливості силового аналізу групи Ассура з поступальною кінематичною парою.

6. Силовий розрахунок ведучої ланки.

Лекція №36

Тема: “Силовий аналіз шарнірного чотириланковика. Метод жорсткого важеля Жуковського”

1. Силовий аналіз шарнірного чотириланковика методом планів сил.

1. Силовий аналіз шарнірного чотириланковика планів сил

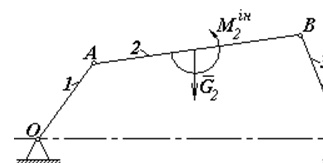
Визначити реакції в кінематичних парах і зрівноважуючий (ведучий) момент від дії сил: , , шарнірного чотириланковика, зображеного на рис.1 у масштабі .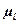

Цей механізм ІІ класу ІІ порядку складається з ведучої групи ОА та однієї групи Ассура АВС.

У зазначеному масштабі 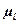накреслимо групу Ассура і нанесемо всі сили, що діють на неї (рис.2,а). Оскільки напрямок реакцій у зовнішніх парах невідомий, розкладаємо їх на нормальну та дотичну (тангенціальну) складові: 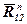, та , .

Складемо умову рівноваги групи Ассура:

.

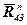Тут невідомими є.

Для визначення дотичних складових складемо рівняння моментів відносно точки В всіх сил, що діють на 2 і 3 ланки окремо:

,

звідки:

.

,

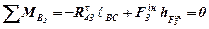звідки:

.

Отже, напрямлена в бік, протилежний тому, що показано на кінематичній схемі. На кінематичній схемі групи Ассура закреслимо її і змінимо напрямок (див. рис.2,а).

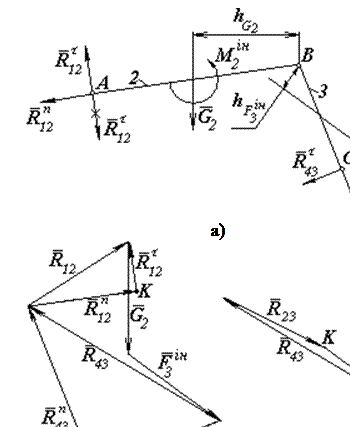
Для визначення нормальних реакцій будуємо план сил за рівнянням рівноваги групи Ассура (рис.2,б)

Повні реакції у відкритих кінематичних парах визначаємо геометричною сумою їх нормальної і дотичної складових:

;

.

Визначимо реакцію в точці В. Для цього складемо рівняння рівноваги третьої ланки (де менше діє сил), маємо:

.

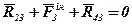За цим рівнянням будуємо план сил (рис.2,в). Як замикальний вектор силового трикутника визначаємо .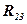

.

Визначимо дійсні значення реакцій:

;

;

.

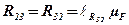Розглянемо ведучу групу ОА. До неї прикладені сили: 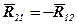, та 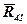(рис.3,а).

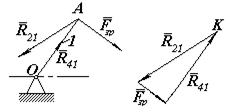
а) б)

Рис.3

Складемо рівняння рівноваги ведучої групи:

.

Вектор відомий за величиною та напрямком, величини 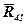та 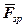визначає точка перетину їх напрямків (рис.3,б).

Дійсні значення сил:

;

.

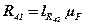Отже, зрівноважуючий момент:

.

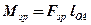2. Метод жорсткого важеля Жуковського

Як ми відзначали вище, метод жорсткого важеля Жуковського застосовується в тому випадку, коли необхідно визначити тільки зрівноважуючу силу і не треба визначати реакцій у кінематичних парах.

Теорема Жуковського. Якщо який-небудь механізм під дією системи сил, прикладених до нього, перебуває у рівновазі, то повернутий на 90⁰ в будь-який бік план швидкостей механізму, який розглядається як жорсткий важіль, що обертається навколо полюса плану і навантажений тими ж силами, прикладеними у відповідних точках плану, теж перебуває у рівновазі.

Цей метод застосовується і для системи, яка не перебуває у рівновазі, досить, крім діючих сил, прикласти сили інерції ланок. Отримана система сил умовно перебуває у рівновазі, тому теорему до неї можна застосувати.

Доведення. В основу доведення покладений принцип можливих переміщень. Жуковський дав графічну інтерпретацію принципу можливих переміщень: робота зведеної сили на її елементарному переміщенні дорівнює сумі робіт реальних сил, що діють у механізмі, на їх елементарних переміщеннях.

Нехай маємо плоский механізм, до ланок якого прикладені відомі сили. Позначимо сили по точках їх прикладання, тобто сила 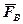прикладена в точці В і т. д.

Зведена сила прикладена в точці А (кінці кривошипа) перпендикулярно до нього.

Як відомо з динаміки матеріальної точки та системи, робота сили обчислюється як добуток сили на елементарне переміщення і косинус кута між напрямами сили і швидкості:

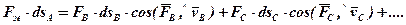(1)

У визначення роботи зведеної сили косинус не ввійшов, оскільки напрямок зведеної сили збігається з напрямком швидкості точки А.

Розділивши рівняння (1) на dt дістанемо:

(2)

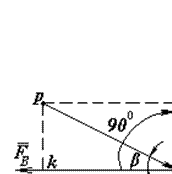Нехай для механізму, на який діють зазначені сили, побудований план швидкостей, на якому є відрізок pb, який зображає швидкість точки В (рис.4). Перенесемо з механізму на план швидкостей у точку b силу . Позначимо кут між напрямками сили і швидкості через β. Тоді:

,

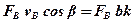де bk – проекція швидкості на напрямок сили , .

Якщо силу 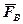повернути на кут 90^○ (у будь-який бік), то проекція швидкості bk стане плечем моменту повернутої сили 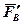відносно полюса р плану швидкостей.

Отже, сума в рівнянні (2) є сумою моментів відносно полюса плану швидкостей всіх сил, перенесених із механізму на план швидкостей і повернутих на кут 90^○.

Якщо в рівнянні (2) добуток перенесемо в праву частину, то він змінить знак на протилежний, тобто зведена сила стане зрівноважуючою, а сума всіх моментів буде дорівнювати 0:

.

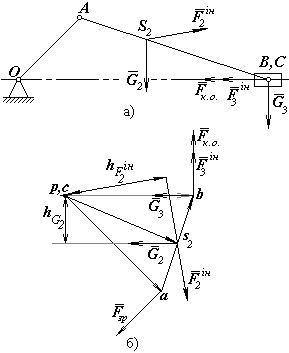
Рис.5

Послідовність визначення зведеної сили методом Жуковського:

1. Будується план швидкостей механізму в масштабі .

2. У відповідних точках плану швидкостей прикладаються повернуті на 90^○ сили, що діють на ланки механізму (включаючи і зрівноважуючу).

3. Складається сума моментів всіх сил відносно полюса плану швидкостей і визначається зрівноважуюча сила.

Розглянемо, як приклад, кривошипно-повзунковий механізм, навантажений у відповідних точках силами: 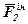, , , , 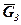. Необхідно визначити зрівноважуючу силу (рис.5, а).

Для цього побудуємо в масштабі план швидкостей механізму (рис.5, б) та прикладемо у точках а, s₂ та в відповідно сили , , 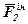та , , 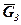, повернуті на кут 90^○ за ходом годинникової стрілки.

Складемо рівняння моментів всіх прикладених до плану швидкостей сил відносно полюса плану:

;

Звідси визначимо шукану зрівноважуючу силу (плечі сил заміряємо безпосередньо на кресленні плану швидкостей):

.

Питання для самоконтролю

1. В якій послідовності ведеться кінематичний аналіз шарнірного чотириланковика?

2. Теорема Жуковського. Доведення.

3. Послідовність визначення зрівноважуючої сили методом Жуковського.

4. Розв’язати задачу силового дослідження шарнірного чотириланковика, застосовуючи метод планів та метод Жуковського.

Лекція №37

Тема: “Тертя в кінематичних парах”

Дата добавления: 2014-10-23