Контрольная работа № 2

ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ ДЛЯ СЛУШАТЕЛЕЙ ЗАЧНОГО ОТДЕЛЕНИЯ

Решение примерного варианта КОНТРОЛЬНОЙ РАБОТЫ

Примерный вариант контрольной работы №2

Задание № 1
по теме "Дифференциальное исчисление функции одной переменной"

1. Найти пределы функции при различных значениях a (не применяя правила Лопиталя):

y = ɑ = 2; ɑ = 1; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

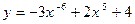2).

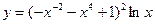
3. Вычислить y' в точке x₀ :

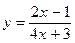; x₀ = – 5.

4. Найти экстремумы функции:

.

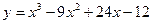5. Найти наибольшее и наименьшее значение функции y на отрезке
[– 4, 4]:

.

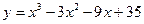6. Вычислить , если:

y = 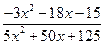; ɑ = – 5.

Задание № 2
по теме "Интегральное исчисление функции одной переменной"

1. Вычислить неопределенный интеграл:

.

2. Вычислить неопределенный интеграл:

.

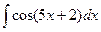3. Вычислить неопределенный интеграл:

.

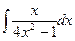4. Вычислить определенный интеграл:

.

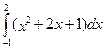5. Вычислить определенный интеграл

.

6. Вычислить определенный интеграл:

.

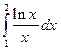7. Решить дифференциальное уравнение:

.

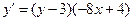8. Решить задачу Коши:

.

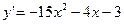
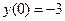Задание № 1
по теме "Дифференциальное исчисление функции одной переменной"

Задача 1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =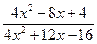; ɑ = 2; ɑ = 1; ɑ ® ¥.

Решение

1. Рассмотрим случай, когда ɑ = 2.

Вычислим предел, пользуясь теоремами о пределах:

.

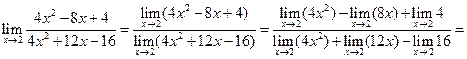
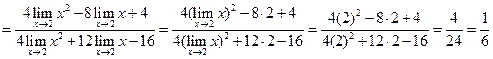2. Рассмотрим случай, когда ɑ = 1.

При 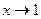числитель и знаменатель дроби стремятся к нулю. В этом случае говорят, что мы имеем неопределенность типа 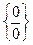и вычисление предела называют раскрытием неопределенности. Для раскрытия неопределенности выполним тождественные преобразования – разложим числитель и знаменатель на множители:

;

.

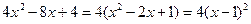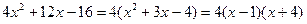Сократим дробь на общий множитель ­ скобку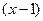

.

Функци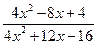и и 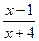совпадают при всех значениях х, отличных от 1 (в окрестности точки х = 1), следовательно, их пределы при 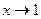равны:

.

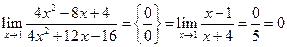3. Рассмотрим случай, когда ɑ ® ¥.

Числитель и знаменатель дроби стремятся к бесконечности при 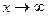, т.е. мы имеем неопределенность типа 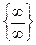. Для раскрытия неопределенности преобразуем дробь, разделив числитель и знаменатель на :

.

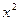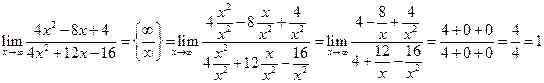Ответ: 1/6; 0; 1.

Задача 2. Вычислить производную функций:

1). ;

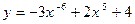2). .

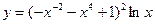Решение

1. Вычислим производную функции, пользуясь правилами дифференцирования (см.формулы (2) – (6)) и таблицей производных для основных элементарных функций (см. таб.1):

.

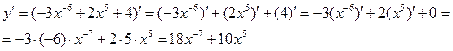2. Вычислим производную функции, пользуясь правилами дифференцирования, таблицей производных и теоремой о дифференцировании сложной функции (8):

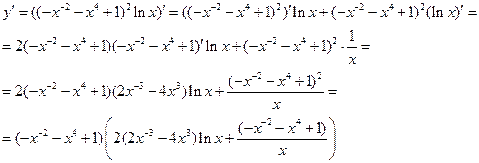
Ответ: 1) ; 2) .

Задача 3. Вычислить y' в точке x₀:

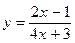; x₀ = – 5.

Решение

1. Пользуясь правилами дифференцирования ((2) – (6)), найдем производную, как функцию от х:

=

=.

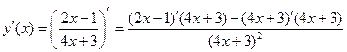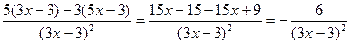2. Вычислим производную в точке x₀ = 5.

.

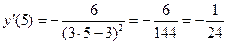Ответ: .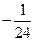

Задача 4. Найти экстремумы функции .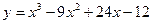

Решение

1. Найдем производную функции

.

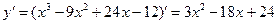2. Производная существует при любых значениях х. Найдем критические точки производной из условия :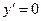

.

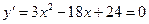Решив квадратное уравнение

,

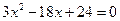получим две критические точки , .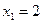

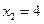3. Определим знаки производной слева и справа от критических точек.

Промежуток	(– 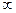, 2)	(2, 4)	(4, )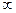
Знак	+	–	+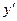
Функция

Знак производной меняется в критических точках 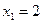, , 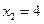следовательно, функция имеет в этих точках экстремумы, а именно: функция имеет максимум в точке 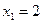(знак 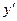меняется с + на –) и минимум в точке 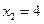(знак 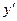меняется с – на +).

4. Определим значения функции в точках минимума и максимума, т.е. в точках , .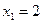

;

.

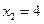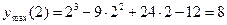Ответ: , .

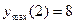Задача 5. Найти наибольшее и наименьшее значение функции 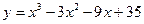на отрезке [– 4, 4].

Решение

1.Найдем экстремумы функции, лежащие внутри отрезка [– 4, 4].

Производная функции

.

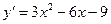Решив уравнение

,

найдем критические точки

,.

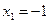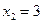Вычислим значения функции в критических точках

; .

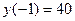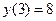2. Вычислим значения функции на концах отрезка [– 4, 4].

; .

3. Сравнивая вычисленные значения функции, находим, что наибольшее значение функции на отрезке [– 4, 4] равно 40 и достигается в критической точке 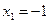, а наименьшее значение равно –41 на конце отрезка, в точке .

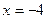Ответ: ; .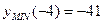

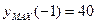Задача 6. Вычислить предел , если:

y = 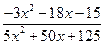; ɑ = – 5.

Решение

При 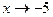числитель и знаменатель данной дроби стремятся нулю, т.е. вычисление предела сводится к раскрытию неопределенности типа 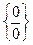и мы можем применить правило Лопиталя (16).

Вычисляя предел по правилу Лопиталя, получим

.

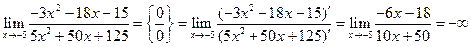Ответ: .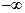

Задание № 2
по теме "Интегральное исчисление функции одной переменной"

Задача 1. Вычислить неопределенный интеграл

.

Решение

Для вычисления интеграла, воспользуемся свойствами неопределенного интеграла ((20) – (24)) и таблицей интегралов (см. таб.2), предварительно представив подынтегральную функцию в виде суммы трех функций:

.

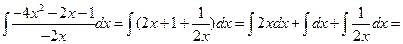
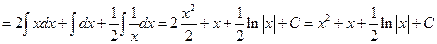Прежде, чем записать ответ, целесообразно сделать проверку. Производная полученной в результате интегрирования функции должна быть равна подынтегральной функции, т.е. должно выполняться
соотношение (17).

Проверка: .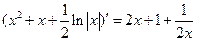

Ответ: .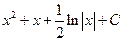

Задача 2. Вычислить неопределенный интеграл .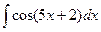

Решение

1. Первый способ. Воспользуемся свойством инвариантности (24). Для этого предварительно вычислим дифференциал 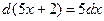. Тогда 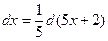и окончательно получим

2. Второй способ. Используем метод замены переменной (метод подстановки). Введем новую переменную

.

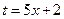Вычислим дифференциал

,

тогда:

,

.

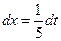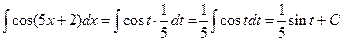Вернемся к старой переменной 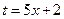(сделаем обратную подстановку)

.

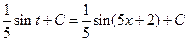Проверка:

.

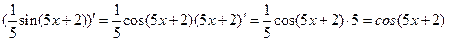Ответ: .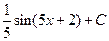

Задача 3. Вычислить неопределенный интеграл .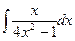

Решение

Заметим, что в исходном интеграле

,

тогда, внося функцию под знак дифференциала, получим

.

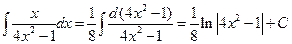Проверка:

.

Ответ: .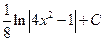

Задача 4. Вычислить определенный интеграл .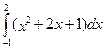

Решение

Вычислим определенный интеграл по формуле
Ньютона-Лейбница (27):

.

Подставляя пределы интегрирования, получим

.

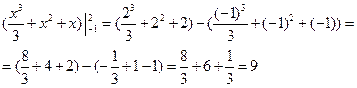Ответ: 9.

Задача 5. Вычислить определенный интеграл .

Решение.

1. Найдем неопределенный интеграл 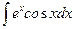, используя метод интегрирования по частям.

В формуле интегрирования по частям (25)

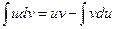
положим

; .

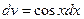тогда

; ,

.

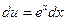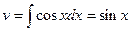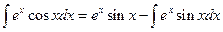Применим интегрирование по частям к последнему интегралу:

.

Таким образом,

,

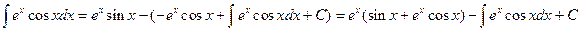откуда окончательно получим

.

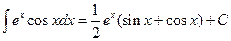2. Вычислим исходный определенный интеграл, подставляя пределы интегрирования в соответствии с формулой Ньютона-Лейбница (27):

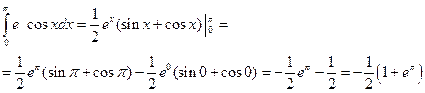
Ответ: .

Задача 6. Вычислить определенный интеграл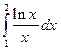

Решение.

Используем метод замены переменной (29). Введем новую переменную:

,

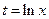вычислим

.

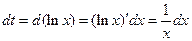Определим новые пределы интегрирования из равенства :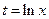

при x = 1 получим ,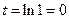

при x = 2 получим .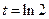

Меняя переменную и вычисляя интеграл по формуле
Ньютона-Лейбница (27), получим:

.

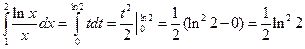Ответ: .

Задача 7. Решить дифференциальное уравнение

.

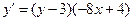Решение.

Исходное уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные, выполняя следующую последовательность действий:

1. Представим в исходном уравнении производную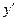в виде :

.

2. Умножим обе части уравнения на :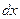

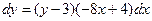
3. Разделим переменные, поделив обе части уравнения на :

.

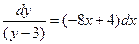4. Проинтегрируем обе части уранения:

,

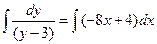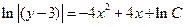[3]

Преобразуем полученное ввыражение

,

,

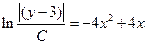откуда получим общее решение уравнения:

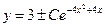
Ответ: .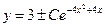

Задача 8. Решить задачу Коши:

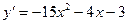;НУ: у (0) = –3.

Решение

1. Найдем общее решение дифференциального уравнения. Так как уравнение является простейшим, то его решение находится интегрированием функции, стоящей в правой части уравнения:

.

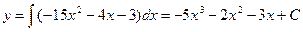2. Найдем значение произвольной постоянной С, соответствующее частному решению дифференциального уравнения, подставляя в общее решение начальное условие у = –3, х = 0:

.

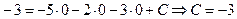3. Запишем частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Для этого подставим найденное значение произвольной постоянной С= –3 в общее решение уравнения:

.

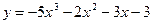Сделаем проверку:

.

Ответ: .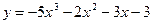

ВАРИАНТ № 1

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =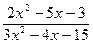 ɑ = 2; ɑ = 3; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

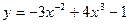2). .

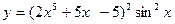3. Вычислить y' в точке x₀ :

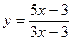; x₀ = 5.

4. Найти экстремумы функции:

.

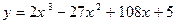5. Найти наибольшее и наименьшее значение функции y на отрезке [0, 7]:

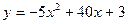
6. Вычислить , используя правило Лопиталя:

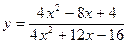; ɑ = 1.

Задание № 2

1. Вычислить неопределенный интеграл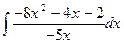

2. Вычислить неопределенный интеграл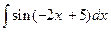

3. Вычислить неопределенный интеграл .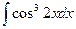

4. Вычислить определенный интеграл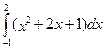

5. Вычислить определенный интеграл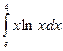

6. Вычислить определенный интеграл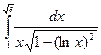

7. Решить дифференциальное уравнение

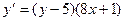
8. Решить задачу Коши: , .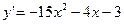

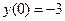ВАРИАНТ № 2

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

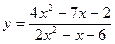ɑ = 0; ɑ = 2; ɑ ® ¥.

2. Вычислить производную функций:

1).

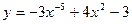
2).

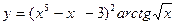
3. Вычислить y' в точке x₀ :

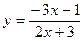; x₀ = – 5.

4. Найти экстремумы функции:

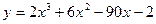
5. Найти наибольшее и наименьшее значение функции y на отрезке [2, 5]:

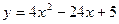
6. Вычислить , используя правило Лопиталя:

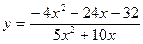; ɑ = – 2.

Задание № 2

1. Вычислить неопределенный интеграл .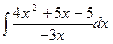

2. Вычислить неопределенный интеграл .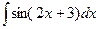

3. Вычислить неопределенный интеграл .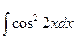

4. Вычислить определенный интеграл .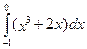

5. Вычислить определенный интеграл .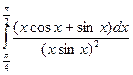

6. Вычислить определенный интеграл .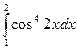

7. Решить дифференциальное уравнение .

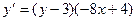8. Решить задачу Коши: , .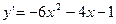

ВАРИАНТ № 3

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

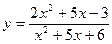ɑ = 3; ɑ = – 3; ɑ ® ¥.

2. Вычислить производную функций:

1).

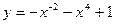
2).

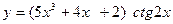
3. Вычислить y' в точке x₀ : 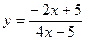; x₀ = 2.

4. Найти экстремумы функции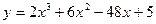

5. Найти наибольшее и наименьшее значение функции y на отрезке
[ – 6, – 3]:

6. Вычислить , используя правило Лопиталя:

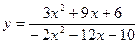; ɑ = – 1.

Задание № 2

1. Вычислить неопределенный интеграл .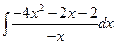

2. Вычислить неопределенный интеграл .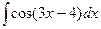

3. Вычислить неопределенный интеграл .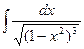

4. Вычислить определенный интеграл .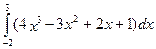

5. Вычислить определенный интеграл .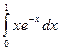

6. Вычислить определенный интеграл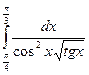

7. Решить дифференциальное уравнение

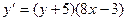
8. Решить задачу Коши: , .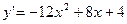

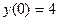ВАРИАНТ № 4

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя).

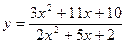ɑ = – 3; ɑ = – 2; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

2). .

3. Вычислить y' в точке x₀ : 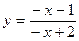; x₀ = 0.

4. Найти экстремумы функции .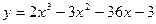

5. Найти наибольшее и наименьшее значение функции y на отрезке
[ – 6, – 3]: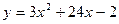

6. Вычислить , используя правило Лопиталя:

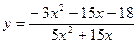; ɑ = – 3.

Задание № 2

1. Вычислить неопределенный интеграл .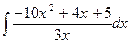

2. Вычислить неопределенный интеграл .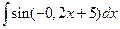

3. Вычислить неопределенный интеграл .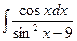

4. Вычислить определенный интеграл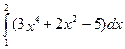

5. Вычислить определенный интеграл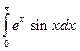

6. Вычислить определенный интеграл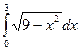

7. Решить дифференциальное уравнение

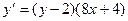
8. Решить задачу Коши: , .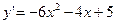

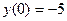ВАРИАНТ № 5

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

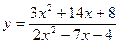ɑ = 2; ɑ = 4; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

2). .

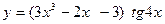3. Вычислить y' в точке x₀ : 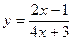; x₀ = – 5.

4. Найти экстремумы функции .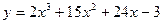

5. Найти наибольшее и наименьшее значение функции y на отрезке
[ – 6, – 1]: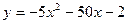

7. Вычислить , используя правило Лопиталя:

; ɑ = – 1.

Задание № 2

1. Вычислить неопределенный интеграл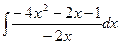

2. Вычислить неопределенный интеграл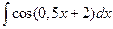

.

3. Вычислить неопределенный интеграл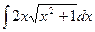

4. Вычислить определенный интеграл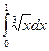

5. Вычислить определенный интеграл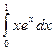

6. Вычислить определенный интеграл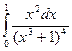

7. Решить дифференциальное уравнение

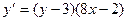
8. Решить задачу Коши: , .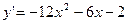

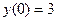ВАРИАНТ № 6

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =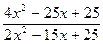 ɑ = 2; ɑ = 5; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

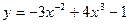2). .

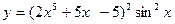3. Вычислить y' в точке x₀ :

; x₀ = 3.

4. Найти экстремумы функции.

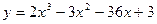
5. Найти наибольшее и наименьшее значение функции y на отрезке
[ – 6, – 2]: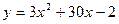

6. Вычислить , используя правило Лопиталя:

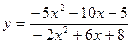; ɑ = – 1.

Задание № 2

1. Вычислить неопределенный интеграл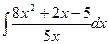

2. Вычислить неопределенный интеграл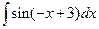

3. Вычислить неопределенный интеграл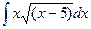

4. Вычислить определенный интеграл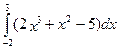

5. Вычислить определенный интеграл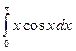

6. Вычислить определенный интеграл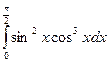

7. Решить дифференциальное уравнение

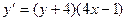
8. Решить задачу Коши: ,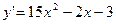

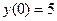
ВАРИАНТ № 7

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =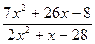 ɑ = 1; ɑ = – 4; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

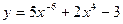2). .

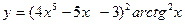3. Вычислить y' в точке x₀ :

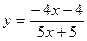; x₀ = 5.

4. Найти экстремумы функции:

.

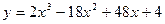5. Найти наибольшее и наименьшее значение функции y на отрезке [2, 9]:

6. Вычислить , используя правило Лопиталя:

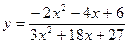; ɑ = –3.

Задание № 2

1. Вычислить неопределенный интеграл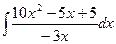

.

2. Вычислить неопределенный интеграл .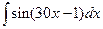

3. Вычислить неопределенный интеграл .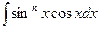

4. Вычислить определенный интеграл .

5. Вычислить определенный интеграл .

6. Вычислить определенный интеграл .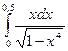

7. Решить дифференциальное уравнение .

8. Решить задачу Коши: , .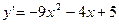

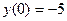ВАРИАНТ № 8

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =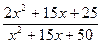 ɑ = 5; ɑ = – 5; ɑ ® ¥.

2. Вычислить производную функций:

1). .

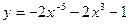2).

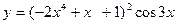
3. Вычислить y' в точке x₀ :

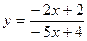; x₀ =3.

4. Найти экстремумы функции:

.

5. Найти наибольшее и наименьшее значение функции y на отрезке [1, 8]:

.

6. Вычислить , используя правило Лопиталя:

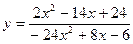; ɑ = 3.

Задание № 2

1. Вычислить неопределенный интеграл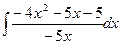

.

2. Вычислить неопределенный интеграл .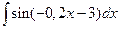

3. Вычислить неопределенный интеграл .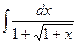

4. Вычислить определенный интеграл .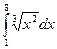

5. Вычислить определенный интеграл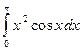

6. Вычислить определенный интеграл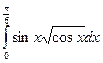

7. Решить дифференциальное уравнение

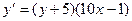
8. Решить задачу Коши: , .

ВАРИАНТ № 9

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =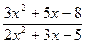 ɑ = – 2; ɑ = 1; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

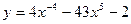2). .

3. Вычислить y' в точке x₀ :

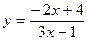; x₀ = – 5.

4. Найти экстремумы функции:

.

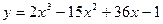5. Найти наибольшее и наименьшее значение функции y на отрезке [2, 6]:

.

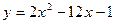6. Вычислить , используя правило Лопиталя:

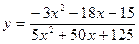; ɑ = – 5.

Задание № 2

1. Вычислить неопределенный интеграл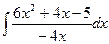

.

2. Вычислить неопределенный интеграл .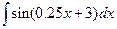

3. Вычислить неопределенный интеграл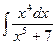

4. Вычислить определенный интеграл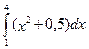

5. Вычислить определенный интеграл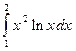

6. Вычислить определенный интеграл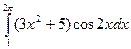

7. Решить дифференциальное уравнение

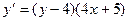
8. Решить задачу Коши: , .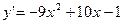

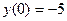ВАРИАНТ № 10

Задание № 1

1. Найти пределы функции при различных значениях ɑ (не применяя правила Лопиталя):

y =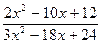 ɑ = 2; ɑ = – 1; ɑ ® ¥.

2. Вычислить производную функций:

1). ;

2). .

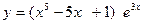3. Вычислить y' в точке x₀ :

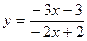; x₀ = 4.

4. Найти экстремумы функции:

.

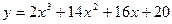5. Найти наибольшее и наименьшее значение функции y на отрезке [–2, 2]:

.

6. Вычислить , используя правило Лопиталя:

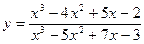; ɑ = 1.

Задание № 2

1. Вычислить неопределенный интеграл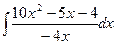

.

2. Вычислить неопределенный интеграл .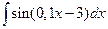

3. Вычислить неопределенный интеграл .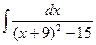

4. Вычислить определенный интеграл .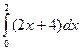

5. Вычислить определенный интеграл .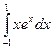

6. Вычислить определенный интеграл .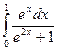

7. Решить дифференциальное уравнение .

8. Решить задачу Коши: , .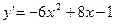

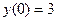РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Н.В.Кожусь. Математика. Курс лекций. ­ СПб: РИО СПб филиала РТА, 2008. - 170 с.

2. Высшая математика для экономистов. Учебник для вузов./Под ред. Проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1998. – 491 с.

3. В.С.Шипачев. Высшая математика. – М.: Высшая школа. 1985.

4. В.С.Шипачев. Задачник по высшей математике: учебное пособие для вузов. – 2-ое изд., М.: Высш. шк., 2001. – 304 с.

5. М.С.Красс. Математика для экономических специальностей. - М.: Инфра. – М. 1998.

6. М.Л.Краснов. Обыкновенные дифференциальные уравнения. М.: Высш. шк. 1983.

7. Н.С.Пискунов. Дифференциальное и интегральное исчисления для втузов. М.: Наука, т.1,2. 1978-1985.

8. С.М.Никольский. Курс математического анализа. - М.: Наука. 1973. т.1. - 432с.; т.2. - 392с.

9. В.И.Смирнов. Курс высшей математики. - М.: Наука. 1974. т.1.-459с.

10. Б.Л.Рождественский. Лекции по математическому анализу. - М.: Наука, 1972. - 544с.

11. П.Е.Данко, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. М.: Высш. шк. 1981 – 1986.

12. Л.С.Понтрягин. Обыкновенные дифференциальные уравнения. М.: Наука, 1982.

13. В.В.Степанов. Курс дифференциальных уравнений. М.: Наука, 1970.

ПРИЛОЖЕНИЕ

Образец оформления титульного листа контрольной работы

Государственное образовательное учреждение высшего профессионального образования «Российская таможенная академия» Санкт-Петербургский имени В.Б.Бобкова филиал Российской таможенной академии _______________________________________________________________ Кафедра информатики и информационных таможенных технологий     КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Вариант № 1
	Выполнил: студент 1курса номер группы заочного отделения экономического факультета И.О.Фамилия   Проверил: И.О.Фамилия Ученая степень, должность
Санкт-Петербург

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

по дисциплине "Математика"

ЧАСТЬ 2

Автор:

Н.В.Кожусь

[1] В приведенной ниже таблице основных интегралов u может обозначать как независимую переменную, так и функцию от независимой переменной, т. е. таблица написана с учетом свойства инвариантности.

[2] Выражение называется знаком двойной подстановки

[3] Заметим, что в данном случае удобнее представить произвольную постоянную в виде.

Дата добавления: 2014-10-23