Квадратичные формы и их приведение к каноническому виду

Пусть в ЛП размерности 2 задан =(х1 х2)T в нормированном евклидовом ортогональном базисе i,j.

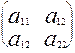
Определение. Выражение ф(х1,х2)= а11х12+2а12 х1 х2 +а22х22=0 где aij - действительные числа, называют квадратичной формой двух переменных х1,х2. Ее можно записать иначе ф(х1,х2)= (а11х1+а12х2) х2+(а12 х1+а22х2)х2. Затем, используя умножение матрицы на вектор получить ф(х1,х2)= =((),)=(Ах,х), причем матрица А – симметрическая и, как известно, ее собственные векторы ортогональны. Пусть это будут векторы 1 и 2. Тогда их можно нормировать и принять в качестве базисных в ортонормированном евклидовом ЛП. Построим единичные векторы в новом базисе (базисе собственных векторов матрицы А). Получаем и - новые единичные. И в этом новом базисе вектор =(х’1 х’2)T. Но в этом случае и квадратичная форма примет новый вид ф(х1,х2)= (А(х’1+ х’2), х’1+ х’2). Но т.к. и - собственные для А, то получаем ф(х1,х2)=((х’1 к1+ х’2 к2), х’1+ х’2)= к1(х’1)2+ к2(х’2)2. Получен новый вид квадратичной формы, в котором отсутствует произведение текущих координат. Такой вид носит название – канонического вида квадратичной формы.

Т.о. в декартовом базисе собственных нормированных векторов матрицы квадратичной формы сама форма принимает канонический вид.

Остается важная задача: установить связь между координатами вектора =(х1 х2)T начального базиса i,j и координатами того же вектора

=(х’1 х’2)T в новом базисе нормированных собственных векторов матрицы квадратичной формы.

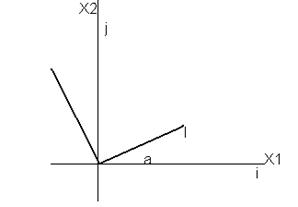
Мы имеем = х1i+х2j = х’1I+х’2J. Но I и J тоже векторы, правда единичной длины. И потому I=iCos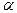 +jCos(90-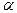), J= iCos 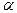+jCos(90+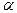). Или после подстановки полученного вместо координат х’1,х’2 получим связь между старыми и новыми координатами = (х’1 х’2)T, которая соответствует матрице поворота плоскости на некоторый угол.

Контрольные вопросы и задания для самостоятельной подготовки:

1. Понятие матрицы.

2. Линейные операции над матрицами.

3. Транспонирование матриц.

4. Произведение матриц.

5. Собственные значения и собственные векторы матриц.

6. Ранг матрицы.

7. Понятие обратной матрицы.

8. Операции над определителями.

9. Свойства определителей.

10. Миноры и алгебраические дополнения.

11. Линейные операторы.

12. Собственные векторы и собственные значения линейного оператора.

13. Понятие квадратичной формы.

14. Преобразование квадратичной формы при замене переменных.

15. Приведение квадратичной формы к каноническому виду.

16. Метод Лагранжа.

17. Закон инерции квадратичных форм.

18. Положительно определенные квадратичные формы. Критерий Сильвестра

19. Найти произведение матриц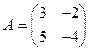

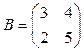
20. Найти матрицу С = -5А - 2В: А =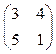 В =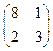

21. Найти матрицу 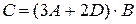, если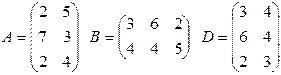

22. Найти обратную матрицу , если

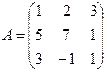
23. Вычислить определитель матрицы

24. Найти матрицу 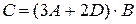, если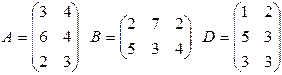

25. Найти обратную матрицу ,если

26. Вычислить определитель матрицы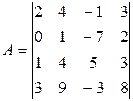

27. Найти матрицу 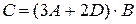, если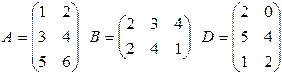

28. Найти обратную матрицу , если

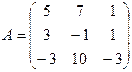
29. Вычислить определитель

30. Найти матрицу , если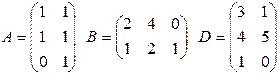

31. Найти обратную матрицу , если

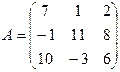
32. Вычислить определитель

33. Вычислить определитель матрицы четвертого порядка: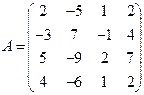

34. Найти матрицу, обратную данной: А =

35. Найти ранг матрицы: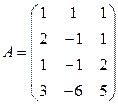

Дата добавления: 2014-10-23