Определение дифференциального уравнения

Тема 11. Дифференциальные уравнения.

Даны основные понятия дифференциальных уравнений. Дифференциальные уравнения первого порядка. Элементы качественного анализа дифференциальных уравнений первого порядка. Неполные дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Дифференциальные уравнения второго порядка, допускающие понижение порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Использование дифференциальных уравнений в экономической динамике.

Многие задачи естествознания формулируются в виде уравнений, в которые входят как неизвестные величины (искомые функции), так и скорости изменения этих величин (т.е. производные искомых функций).

Определение 1. Уравнения, в которых неизвестными являются функции и в которые входят не только сами функции, но и их производные, называются дифференциальными уравнениями.

Определение 2. Порядком дифференциального уравнения называется порядок старшей производной искомой функции, входящей в это уравнение.

Пример. Пусть с некоторой высоты на землю сброшено тело массой т. Требуется найти закон изменения скорости падения v от времени t, т. е. нужно найти функцию v =v (t).

По II закону Ньютона F = ma; F = m 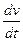(1)

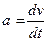- ускорение движущегося тела,

F - результирующая сила, действующая на тело в процессе движения.

В данном случае

F = mg – F_сопр. (2)

mg - сила тяжести, F_сопр. - сила сопротивления воздуха.

Известно, что при обтекаемой форме тела и не слишком больших скоростях движения величина F_сопр. пропорциональна скорости движения тела, т.е.

F_сопр. = 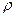v (3)

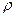- коэффициент пропорциональности.

Подставим формулы (2) и (3) в уравнение (1):

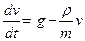(4) - дифференциальное уравнение 1- го порядка,

описывающее падение тела в воздушной среде. Решив уравнение (4), найдем функцию v=v(t),обращающую это уравнение в тождество по независимой переменной t на некотором интервале (а;в),т.е. найдем искомый закон изменения скорости падающего тела.

В общем случае дифференциальное уравнение первого порядка можно записать в виде F(x,y,)=0, где у=у(х) - искомая неизвестная функция, 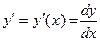- ее производная по независимой переменной х, а F – заданная функция трех переменных .

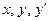На практике чаще встречаются уравнения, разрешенные относительно производной

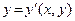
(1)

Определение. Функция у=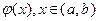, называется решением дифференциального уравнения (1), если справедливо равенство

Когда функция f в уравнении (1) зависит только от переменной х, получается простейшее дифференциальное уравнение первого порядка

Задача отыскания решений этого уравнения – это задача о нахождении первообразных функции f(x), т.е. задача вычисления неопределенного интеграла .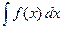

Итак, решение простейшего дифференциального уравнения имеет вид:

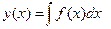или .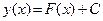

Таким образом, простейшее дифференциальное уравнение первого порядка имеет бесконечное множество решений.

Определение. Функция 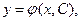которая при каждом фиксированном значении С как функция от является решением дифференциального уравнения (1), называется общим решением дифференциального уравнения (1).

Пример. ;

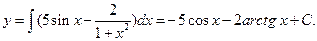
Определение.. Каждое решение дифференциального уравнения, которое получается из общего решения при конкретном значении постоянной интегрирования С, называется частным решением.

Для выделения единственного решения из общего решения дифференциального уравнения применяют дополнительное услови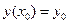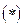е , где 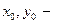заданные числа.

Условие называется начальным условием.

Определение.Задача нахождения решения дифференциального уравнения 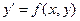, удовлетворяющего начальному условию , называется задачей Коши.

Дата добавления: 2014-10-23