Оценка погрешности метода Монте-Карло

Моделирование случайных величин методом Монте-Карло (статистических испытаний).

Задачу, для решения которой применяется метод Монте-Карло, можно сформулировать так: требуется найти значение а изучаемой случайной величины. Для его определения выбирается случайная величина Х, математическое ожидание которой равно а, и для выборки из п значений Х, полученных в п испытаниях, вычисляется выборочное среднее:

,

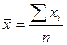которое принимается в качестве оценки искомого числа а:

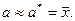
Этот метод требует проведения большого числа испытаний, поэтому его иначе называют методом статистических испытаний. Теория метода Монте-Карло исследует, как наиболее целесообразно выбрать случайную величину Х, как найти ее возможные значения, как уменьшить дисперсию используемых случайных величин, чтобы погрешность при замене а на а * была возможно меньшей.

Поиск возможных значений Х называют разыгрыванием случайной величины. Рассмотрим некоторые способы разыгрывания случайных величин и выясним, как оценить допускаемую при этом ошибку.

Если поставить задачу определения верхней границы допускаемой ошибки с заданной доверительной вероятностью g, то есть поиска числа d, для которого

,

то получим известную задачу определения доверительного интервала для математичес-кого ожидания генеральной совокупности (см. лекцию 18). Воспользуемся результатами решения этой задачи для следующих случаев:

1) случайная величины Х распределена нормально и известно ее среднее квадратическое отклонение. Тогда из формулы (18.1) получаем: 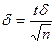, где п – число испытаний, s - известное среднее квадратическое отклонение, а t – аргумент функции Лапласа, при котором Ф(t) = g/2.

2) Случайная величина Х распределена нормально с неизвестным s. Воспользуемся формулой (18.3), из которой следует, что 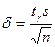, где s – исправленное выборочное среднее квадратическое отклонение, а определяется по соответствующей таблице.

3) Если случайная величина распределена по иному закону, то при достаточно большом количестве испытаний (n > 30) можно использовать для оценки d предыдущие формулы, так как при п ®¥ распределение Стьюдента стремится к нормальному, и границы интервалов, полученные по формулам, различаются незначительно.

Дата добавления: 2014-10-23