
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 1 Матрицы. Действия с матрицами
|
|
|
|
Линейная алгебра
СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
2.1. Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | |
| Обязательная аудиторная учебная нагрузка (всего) | |
| в том числе: | |
| лабораторные работы | - |
| практические занятия | - |
| контрольные работы | - |
| курсовая работа (проект) | - |
| Самостоятельная работа обучающегося (всего) | - |
| Итоговая аттестация: экзамен |
2.2. Тематический план и содержание учебной дисциплины “Математика”
| Наименование разделов и тем | Содержание учебного материала, самостоятельная работа обучающихся | Объем часов | Уровень освоения | ||||
| Раздел 1 Линейная алгебра | |||||||
| Содержание учебного материала | |||||||
| Матрицы. Действия с матрицами. Сложение и умножение матриц. | |||||||
| Определители. Вычисления определителей 2 и 3 порядков. | |||||||
| Раздел 2 Понятие числа | Содержание учебного материала | ||||||
| Комплексные числа. Действия с комплексными числами. | |||||||
| Возведение комплексных чисел в степень. Извлечение из корня комплексных чисел. | |||||||
| Раздел 3 Корни. Степени | Содержание учебного материала | ||||||
| Корень п-ой степени. Преобразование степенных выражений с рациональными показателями. | |||||||
| Способы решения систем линейных уравнений методом Крамера. | |||||||
| Раздел 4 Уравнения и неравенства | Содержание учебного материала | ||||||
| Линейные уравнения, неравенства. | |||||||
| Простейшие показательные уравнения и неравенства. | |||||||
| Раздел 5 Элементы математической статистики | Содержание учебного материала | ||||||
| Основные понятия комбинаторики. | |||||||
| Генеральная совокупность, выборка, медиана, среднее арифметическое. | |||||||
Раздел 1
|
|
|
Цель, форма работы: отработать навыки сложения, вычитания и умножения, закрепление и систематизация знаний по теме;
Краткое изложение теоретических вопросов:
1.Матрица. Элементы матрицы.
Пусть дана таблица из 4 чисел

|
| Это матрица. Она имеет две строки и два столбца, т.е. размер матрицы (2х2). Числа, составляющие эту матрицу, обозначены буквой с двумя индексами. Первый индекс указывает номер строки, а второй — номер столбца, в которой стоит данное число. Например, а12 означает число, стоящее в первой строке и втором столбце; а21 – число, стоящее во второй строке и первом столбце. Числа а11, а12, а21, а22 будем называть элементами матрицы. |
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов. Для записи матрицы используется следующее обозначение:
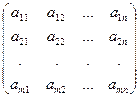 Для любого элемента
Для любого элемента 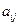 , первый индекс i означает номер строки, а второй индекс j - номер столбца. Сокращенно прямоугольную матрицу типа , первый индекс i означает номер строки, а второй индекс j - номер столбца. Сокращенно прямоугольную матрицу типа 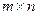 можно записать так: A =( можно записать так: A =(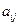 ), где i =1, 2,..., m; j =1, 2,..., n.
2. Виды матриц. Векторы
Если число строк матрицы не равно числу столбцов ( ), где i =1, 2,..., m; j =1, 2,..., n.
2. Виды матриц. Векторы
Если число строк матрицы не равно числу столбцов ( ), то матрица называется прямоугольной. Таковы, например, матрицы
A = ), то матрица называется прямоугольной. Таковы, например, матрицы
A = 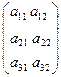 , B = , B = 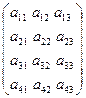 Если число строк равно числу столбцов (m = n), то матрица называетсяквадратной. Например, квадратными являются матрицы
A =
Если число строк равно числу столбцов (m = n), то матрица называетсяквадратной. Например, квадратными являются матрицы
A = 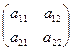 , B = , B = 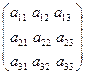 Число строк или столбцов квадратной матрицы называется еепорядком. Так, в последнем примере порядок матрицы А равен 2, а порядок матрицы В равен 3.
Рассмотрим квадратную матрицу порядка 4:
Число строк или столбцов квадратной матрицы называется еепорядком. Так, в последнем примере порядок матрицы А равен 2, а порядок матрицы В равен 3.
Рассмотрим квадратную матрицу порядка 4:  Диагональ, содержащую элементы
Диагональ, содержащую элементы 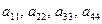 будем называтьглавной, а диагональ, содержащую элементы будем называтьглавной, а диагональ, содержащую элементы 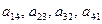 -побочной
Среди квадратных матриц выделим матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали: -побочной
Среди квадратных матриц выделим матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали: 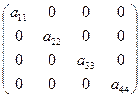 Такие матрицы называютсядиагональными; например, матрицы
A =
Такие матрицы называютсядиагональными; например, матрицы
A = 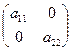 , B = , B = 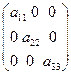 являются диагональными матрицами второго и третьего порядка.
Если у диагональной матрицы все числа главной диагонали равны между собой, то такая диагональная матрица называется скалярной. Например, A =
являются диагональными матрицами второго и третьего порядка.
Если у диагональной матрицы все числа главной диагонали равны между собой, то такая диагональная матрица называется скалярной. Например, A = 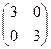 .
Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной и обозначается буквой Е: Е = .
Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной и обозначается буквой Е: Е = 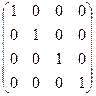 .
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается так: О = .
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается так: О = 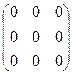 .
В прямоугольной матрице типа .
В прямоугольной матрице типа 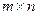 возможен случай, когда m = 1. При этом получается матрица-строка: A = возможен случай, когда m = 1. При этом получается матрица-строка: A = 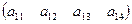 .
В случае, когда n = 1, получаем матрицу-столбец: В = .
В случае, когда n = 1, получаем матрицу-столбец: В = 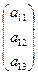 .
Матрицы-строки и матрицы-столбцы называют векторами.
3. Равенство матриц
Две матрицы называются равными, если они имеют одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны. Так, матрицы
A = .
Матрицы-строки и матрицы-столбцы называют векторами.
3. Равенство матриц
Две матрицы называются равными, если они имеют одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны. Так, матрицы
A =  и В = и В = 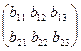 равны, если равны, если 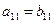 , , 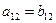 , ,  , , 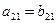 , , 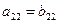 , , 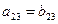 .
Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа .
Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа 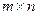 , либо квадратные одного и того же порядка n.
Если в матрице переставить строки со столбцами, получим матрицу, которую будем называть транспонированной матрицей.
Например, матрицы А и В являются транспонированными
А = , либо квадратные одного и того же порядка n.
Если в матрице переставить строки со столбцами, получим матрицу, которую будем называть транспонированной матрицей.
Например, матрицы А и В являются транспонированными
А =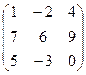 ; В = ; В =  .
В том случае, когда матрица состоит из одной строки (матрица-строка), т. е.
B= .
В том случае, когда матрица состоит из одной строки (матрица-строка), т. е.
B=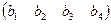 , транспонированная матрица является матрицей-столбцом: Bт = , транспонированная матрица является матрицей-столбцом: Bт = 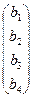 .
4. Линейные операции над матрицами
Суммой матриц А и В называют такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковое строение: или прямоугольные типа .
4. Линейные операции над матрицами
Суммой матриц А и В называют такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковое строение: или прямоугольные типа 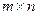 , или квадратные порядка n.
Пусть A = , или квадратные порядка n.
Пусть A = 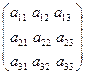 , B = , B = 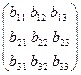 .
Тогда сумма матриц С = A+B имеет вид
C = .
Тогда сумма матриц С = A+B имеет вид
C =  .
ЗАДАНИЕ. Сложить матрицы А и В, если:
а) А = .
ЗАДАНИЕ. Сложить матрицы А и В, если:
а) А = 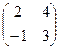 , В = , В =  ;
б) А = ;
б) А = 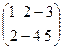 , В = , В =  ;
в) А = ;
в) А = 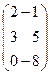 , В = , В = 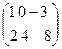 .
Решение,
а) Здесь А и В - квадратные матрицы второго порядка. Складывая их соответствующие элементы, получим
С = А+В = .
Решение,
а) Здесь А и В - квадратные матрицы второго порядка. Складывая их соответствующие элементы, получим
С = А+В = 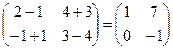 .
б) Здесь А и В - прямоугольные матрицы типа 2 .
б) Здесь А и В - прямоугольные матрицы типа 2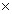 3. Складываем их соответствующие элементы: С = А + В = 3. Складываем их соответствующие элементы: С = А + В = 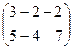 .
в) Эти прямоугольные матрицы сложить нельзя, так как А есть матрица типа 3 .
в) Эти прямоугольные матрицы сложить нельзя, так как А есть матрица типа 3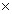 2, а В - матрица типа 2 2, а В - матрица типа 2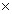 3; можно складывать только прямоугольные матрицы одного типа.
Мы видим, что сложение матриц сводится непосредственно к сложению их элементов, являющихся числами. Поэтому на сложение матриц распространяются важнейшие свойства чисел:
1) переместительный закон сложения: А+В=В+А, где А и В - либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа 3; можно складывать только прямоугольные матрицы одного типа.
Мы видим, что сложение матриц сводится непосредственно к сложению их элементов, являющихся числами. Поэтому на сложение матриц распространяются важнейшие свойства чисел:
1) переместительный закон сложения: А+В=В+А, где А и В - либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа 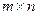 ;
2) сочетательный закон сложения (A+В)+С=A+(B+С), где А, В, С - либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа ;
2) сочетательный закон сложения (A+В)+С=A+(B+С), где А, В, С - либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа 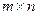 .
3) поглощательный закон сложения А+0=А, т. е. существует такая нулевая матрица (того же порядка или типа), что ее сумма с матрицей А любого типа равна матрице А.
Для любой матрицы А существует матрица -А, такая, что А+(- А) = 0,т.е. матрица, противоположная А.
Произведением матрицы А на число k называется такая матрица kA, каждый элемент которой равен kaij, т. е. если А = .
3) поглощательный закон сложения А+0=А, т. е. существует такая нулевая матрица (того же порядка или типа), что ее сумма с матрицей А любого типа равна матрице А.
Для любой матрицы А существует матрица -А, такая, что А+(- А) = 0,т.е. матрица, противоположная А.
Произведением матрицы А на число k называется такая матрица kA, каждый элемент которой равен kaij, т. е. если А = 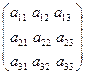 , то кА = , то кА = 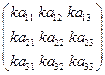 .
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
ЗАДАНИЕ. Умножить матрицу А = .
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
ЗАДАНИЕ. Умножить матрицу А = 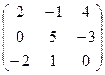 на число k = 3.
Решение. Умножая каждый элемент матрицы А на 3, получим
3А = на число k = 3.
Решение. Умножая каждый элемент матрицы А на 3, получим
3А = 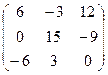 .
5. Умножение матриц.
Рассмотрим умножение квадратных матриц второго порядка.
Пусть А = .
5. Умножение матриц.
Рассмотрим умножение квадратных матриц второго порядка.
Пусть А = 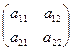 , В = , В = 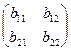 Произведением этих матриц называется матрица
С = АВ =
Произведением этих матриц называется матрица
С = АВ = 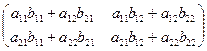 .
Правило нахождения матрицы-произведения распространяется на умножение прямоугольных матриц.
Для прямоугольных матриц справедливы следующие правила:
1) умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В;
2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
6. Свойства умножения матриц
1) Произведение двух матриц не подчиняется переместительному закону, т. е. АВ .
Правило нахождения матрицы-произведения распространяется на умножение прямоугольных матриц.
Для прямоугольных матриц справедливы следующие правила:
1) умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В;
2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
6. Свойства умножения матриц
1) Произведение двух матриц не подчиняется переместительному закону, т. е. АВ ВА.
2) Для умножения матриц выполняется сочетательный закон: А(ВС)=(АВ)С.
3) Выполняется распределительный закон: (А+В)С=АС+ВС.
ЗАДАНИЯ
1. Вычислить линейные комбинации матриц 2А + 3В - С, если
А = ВА.
2) Для умножения матриц выполняется сочетательный закон: А(ВС)=(АВ)С.
3) Выполняется распределительный закон: (А+В)С=АС+ВС.
ЗАДАНИЯ
1. Вычислить линейные комбинации матриц 2А + 3В - С, если
А = 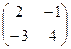 , В = , В = 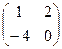 , С = , С = 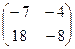 . Ответ: . Ответ: 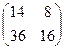 .
2. Найти произведение матриц:
а) .
2. Найти произведение матриц:
а) 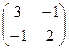 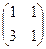 . Ответ: . Ответ: 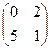 .
б) .
б) 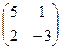 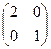 . Ответ: . Ответ: 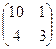 .
в) .
в) 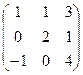 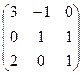 . Ответ: . Ответ: 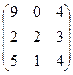 .
Тема 2. Вычисление определителя разложением по первой строке.
Цель, форма работы: отработать навыки вычисления определителя разложением по первой строке; систематизация знаний по данной теме.
Определителем второго порядка (соответствующим данной матрице) называется число .
Тема 2. Вычисление определителя разложением по первой строке.
Цель, форма работы: отработать навыки вычисления определителя разложением по первой строке; систематизация знаний по данной теме.
Определителем второго порядка (соответствующим данной матрице) называется число
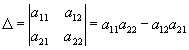 1. Разложение определителя по первой строке имеет вид:
1. Разложение определителя по первой строке имеет вид:
 × ×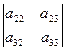 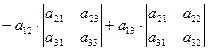 На практике удобно пользоваться схемами знаков алгебраических дополнений:
На практике удобно пользоваться схемами знаков алгебраических дополнений:
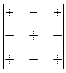 -для определителя третьего порядка;
2.Свойства определителя третьего порядка.
При вычислении определителей удобно пользоваться следующими ихсвойствами:
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонирование).
2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.
3. Определитель, имеющий две линейно зависимые (пропорциональные) строки (столбца) равен нулю. В частности, определитель, имеющий две одинаковые строки (столбца) равен нулю.
4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя. В частности, определитель, имеющий нулевую строку (столбец), равен нулю.
5. Значение определителя не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, отличное от нуля
3.Примеры вычисления определителей.
1. Значение определителя равно: -для определителя третьего порядка;
2.Свойства определителя третьего порядка.
При вычислении определителей удобно пользоваться следующими ихсвойствами:
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонирование).
2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.
3. Определитель, имеющий две линейно зависимые (пропорциональные) строки (столбца) равен нулю. В частности, определитель, имеющий две одинаковые строки (столбца) равен нулю.
4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя. В частности, определитель, имеющий нулевую строку (столбец), равен нулю.
5. Значение определителя не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, отличное от нуля
3.Примеры вычисления определителей.
1. Значение определителя равно: 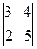 1) 7 2) 0 3) 23 4) -7
2. Значение определителя равно:
1) 7 2) 0 3) 23 4) -7
2. Значение определителя равно:  1) 14 2) -14 3) 0 4) 73
3. Значение определителя равно:
1) 14 2) -14 3) 0 4) 73
3. Значение определителя равно: 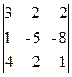 1) 11 2) 0 3) -8 4) -11
4. Значение определителя равно:
1) 11 2) 0 3) -8 4) -11
4. Значение определителя равно: 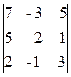 1) 43 2) -18 3) 15 4) -16
5. Значение определителя равно:
1) 43 2) -18 3) 15 4) -16
5. Значение определителя равно:  1) -43 2) 0 3) 58 4) 86
Пример 4. Найти значения определителей:
а)
1) -43 2) 0 3) 58 4) 86
Пример 4. Найти значения определителей:
а) 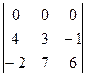 ; б) ; б) 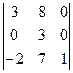 Решение:
а) имеется нулевая строка; согласно свойству 4 определитель равен 0;
б) разложим определитель по элементам третьего столбца:
Решение:
а) имеется нулевая строка; согласно свойству 4 определитель равен 0;
б) разложим определитель по элементам третьего столбца:
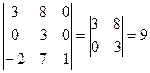 ;
Пример 5. Вычислить определитель: ;
Пример 5. Вычислить определитель:
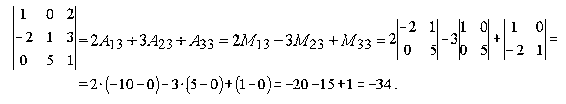 Пример 6. Вычислить определитель:
Пример 6. Вычислить определитель: 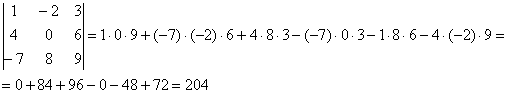 Пример 7. Вычислить определитель:
Пример 7. Вычислить определитель: 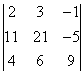
|
Раздел 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 1284; Нарушение авторских прав?; Мы поможем в написании вашей работы!