Тема: похибки чисельного інтегрування, метод кратного перерахунку

Лабораторна робота 16.

Завдання.

Контрольні питання.

1. Чому не завжди для інтегрування функції можна скористатися формулою Ньютона – Лейбниця?

2. Дайте визначення квадратурної формули, вузлів і коефіцієнтів квадратурної формули.

3. Доведіть квадратурну формулу трапецій.

4. Чому дорівнюють вузли і коефіцієнти квадратурної формули Сімпсона?

5. Що таке узагальнені квадратурні формули? Навіщо вони потрібні?

6. Чому дорівнюють вузли і коефіцієнти узагальненої квадратурної формули трапецій?

7. Чому дорівнюють вузли і коефіцієнти узагальненої квадратурної формули Сімпсона?

8. Яка відповідь задачі 1? задачі 2?

Задача. Обчисліть наближені значення наступної функції на відрізку [0;1] за узагальненою формулою трапецій та узагальненою формулою Сімпсона з кроками інтегрування h = 0,5 0,25 0,125. Порівняйте отримані результати.

Варіант	Функція
	e^xcosx
	x^2e^-x
	x^2arctgx
	e^sinxsin2x
	e^x/(1+x)
	(1+x)^3/2e^-x
	e^x/(3+2cosx)
	e^cosx(1+x)
	(1+x)ln^2(1+x)

(2г.)

Мета: Отримати відомості про апостеріорні методи оцінки точності чисельного

інтегрування та навчитися застосовувати ці методи до конкретних задач.

Теоретичні відомості.

Розглянемо квадратурну формулу ≈ .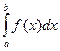

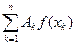Означення 1. Різницю R_n(f) між визначеним інтегралом і квадратурною сумою R_n(f) = 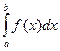– 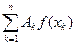називають залишковим членом або похибкою квадратурної формули.

Точність квадратурної формули звичайно характеризують порядком її залишкового члена R(f) стосовно степеня відстані між вузлами інтегрування h, тобто стосовно кроку інтегрування.

Означення 2. З алишковий член R(f) квадратурної формули має порядок k (де k – натуральне число) відносно кроку інтегрування h, якщо існують такі сталі С, с > 0, що ch^k ≤ ôR(f)ô ≤ Сh^k для всіх достатньо малих h.

Записують це так: R(f) = О(h^k). Якщо крок h достатньо малий, то квадратурна формула тим точніша, чим більшим є порядок її залишкового члена.

Для будь – якої квадратурної формули і довільного натурального n можна побудувати на відрізку [a; b] відповідну узагальнену квадратурну формулу, поділивши [a; b] на n рівних відрізків і на кожному з них застосувавши дану квадратурну формулу. Залишковий член узагальненої квадратурної формули трапецій має другий порядок: R_у(f) = О(h²), а узагальненої квадратурної формули Сімпсона четвертий: R_у(f) = О(h⁴).

Застосуємо тут апостеріорні (тобто отримані після і в результаті розрахунків) методи оцінки точності квадратурних формул. Нехай залишковий член деякої узагальненої квадратурної формули має порядок р відносно кроку інтегрування h: R(f) = О(h^р). Поділимо відрізок [a; b] на n рівних відрізків і на 2n рівних відрізків, нехай I_n та I_2n – наближені значення інтеграла 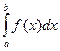за відповідними узагальненими квадратурними формулами, а R_n(f) і R_2n(f) – відповідні залишкові члени. Апостеріорний метод подвійного перерахунку ґрунтується на двох формулах.

1. R_2n (f) ≈ (правило Рунге) (1)

2. 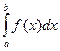≈ I_n,2n = I_2n + (формула екстраполяції за Річардсоном). (2)

Тут похибка R_2n(f) = О(h^p+1), 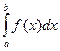= I_n,2n + О(h^p+1). Процес можна продовжити: поділити відрізок [a; b] ще на 4n рівних відрізків і дістати за правилом Рунге та формулою екстраполяції за Річардсоном I_2n,4n і R_4n (f), які є вже наближеннями порядку р + 2 і так далі, отримуючи наближення порядку р + 3, р + 4, …. Це складає апостеріорний метод кратного перерахунку, який є узагальненням методу подвійного перерахунку.

Хід роботи.

Задача 1. 1. Обчислити наближене значення інтеграла функції f (x) = e^{sin x} cos2x на відрізку [0;1] за узагальненою формулою трапецій з кроками інтегрування h = 0,2 0,1 0,05.

2. Уточнити значення інтеграла і оцінити його похибку методом кратного перерахунку.

Розв’язання. 1. Завдання 1. виконано уже в лабораторній роботі 15. Будемо спиратися далі на ці підрахунки.

2. Переформуємо дещо останню електронну таблицю задачі 1 лабораторної роботи 15 у таблицю кратного перерахунку. Надамо чарункам таких значень:

	A	B	C	D
	№ перерахунку
	n	s	I	R
		= СУММПРОИЗВ(B2:B7;C2:C7)	= 0,5/A26*B26
		= СУММПРОИЗВ(F2:F12;G2:G12)	↓	= 1/3*(C27-C26)
		= СУММПРОИЗВ(K2:K22;L2:L22)	↓	↓

Тут у стовпці А n – кількість відрізків, на які вузли інтегрування ділять [0;1] (1/n = h), яка подвоюється згідно з методом кратного перерахунку. У стовпці В інтегральна сума, у стовпці С – відповідне наближене значення інтеграла згідно з узагальненою формулою трапецій. У стовпці D підрахунок оцінки похибки отриманого значення інтеграла згідно з правилом Рунге (1). Оскільки в узагальненої формули трапецій порядок р дорівнює 2, то тут ділимо на 3 = 2^р – 1. В результаті маємо таку таблицю:

	A	B	C	D
	№ перерахунку
	n	s	I	R
		5,493444	0,549344
		11,27574	0,563787	0,004814
		22,69522	0,567381	0,001198

З таблиці знаходимо I₅ ≈ 0,549344, I₁₀ ≈ 0,563787, I₂₀ ≈ 0,567381; R₁₀ (f) ≈ 0,004814, R₂₀ (f) ≈ 0,001198. Як бачимо, із зростанням n, тобто зменшенням кроку h = 1/n значення R(f) зменшується. Тепер розширимо попередню таблицю направо і проведемо в ній такі перерахунки. Надамо чарункам таких значень:

	A	B	C	D	E	F	G
	№ перерахунку
	n	s	I	R	I	R	I
		*	*
		*	↓	*	= C27 + D27
		*	↓	↓	↓	= 1/7*(E28 – E27)	= E28 + F28

Символ * у чарунці цієї таблиці означає, що в ній залишилась та ж сама формула, що була до розширення. Далі у стовпці Е знаходимо уточнені значення інтеграла по формулі екстраполяції за Річардсоном (2), тобто значення I_n,2n та I_2n,4n уже порядку 3. Цим започаткований другий перерахунок, а тому в чарунці F28 обчислюємо оцінку похибки знову за правилом Рунге (1): із зростанням кратності перерахунку на одиницю порядок р теж зростає на одиницю і отже при другому перерахунку р = 3, 2^р – 1 = 7. Нарешті у чарунці G28 обчислюємо наближене значення інтегралу з залишковим членом порядку 4 за формулою Річардсона (2). В результаті обчислення в Excel дістаємо таблицю:

	A	B	C	D	E	F	G
	№ перерахунку
	n	s	I	R	I	R	I
		5,493444	0,549344
		11,27574	0,563787	0,004814	0,568601
		22,69522	0,567381	0,001198	0,568578	-7,7E-06	0,568571

Як бачимо з чарунки F28, отримане значення похибки значно краще очікуваного для порядку 3: насправді метод гарантує лише не гірші результати. Отже, наближене значення інтеграла в G28 уже навіть порядку 5 (а не 4), як ми розраховували.

Задача 2. Обчислити наближене значення функції f (x) = e^xsinx на відрізку [0;1] за узагальненою формулою Сімпсона з точністю 10^-8, для оцінки похибки використавши метод кратного перерахунку.

Розв’язання. У задачі 2 лабораторної роботи 15 були вже обчислені наближені значення функції f (x) = e^xsinx на відрізку [0;1] за узагальненою формулою Сімпсона з кроками інтегрування h = 0,5 0,25 0,125. Будемо спиратися далі на ці підрахунки. Переформуємо дещо останню електронну таблицю задачі 2 лабораторної роботи 15 у таблицю кратного перерахунку. Надамо чарункам таких значень:

	A	B	C	D
	№ перерахунку
	n	s	I	R
		= СУММПРОИЗВ(B2:B4;C2:C4)	= B16/(3*А16)
		= СУММПРОИЗВ(F2:F6;G2:G6)	↓	= 1/15*(C17-C16)
		= СУММПРОИЗВ(K2:K10;L2:L10)	↓	↓

Тут у стовпці А n – кількість відрізків, на які вузли інтегрування ділять [0;1] (1/n = h), яка подвоюється згідно з методом кратного перерахунку. У стовпці В інтегральна сума, у стовпці С – відповідне наближене значення інтеграла згідно з узагальненою формулою Сімпсона. У стовпці D підрахунок оцінки похибки отриманого значення інтеграла згідно з правилом Рунге (1). Оскільки в узагальненої формули Сімпсона порядок р дорівнює 4, то тут ділимо на 15 = 2^р – 1. В результаті маємо таку таблицю:

	A	B	C	D
	№ перерахунку
	n	s	I	R
		5,449112	0,908185
		10,91104	0,909254	7,12176E-05
		21,82382	0,909326	4,81561E-06

З таблиці знаходимо I₂ ≈ 0,908185, I₄ ≈ 0,909254, I₈ ≈ 0,909326; R₄ (f) ≈ 7,12176E-05, R₈(f) ≈ 4,81561E-06. Як бачимо, отримані наближені значення інтегралу є недостатньо точними. Тому розширимо попередню таблицю направо і проведемо у ній другий перерахунок:

	A	B	C	D	E	F
	№ перерахунку
	n	s	I	R	I	R
		*	*
		*	↓	*	= C17 + D17
		*	↓	↓	↓	= 1/31*(E18 – E17)

Символ * у чарунці цієї таблиці означає, як і раніше, що в ній залишилась та ж сама формула, що була до розширення. Далі у стовпці Е знаходимо уточнені значення інтеграла за формулою (2), тобто значення I_n,2n та I_2n,4n наступного порядку, в чарунці F18 оцінку похибки знову за правилом Рунге (1). Отже, дістаємо таблицю:

	A	B	C	D	E	F
	№ перерахунку
	n	s	I	R	I	R
		5,449112	0,908185
		10,91104	0,909254	7,12176E-05	0,909325
		21,82382	0,909326	4,81561E-06	0,909331	1,88137E-07

Отже, похибка ≈ 1,88137E-07. Порядок похибки зріс на одиницю, проте отримані наближені значення інтегралу все ще є недостатньо точними. Порядок зростає як із зростанням кількості перерахунків, так і із зростанням n. Оскільки всі можливості збільшення кількості перерахунків вичерпані при даних n, то треба покласти n = 16 і провести відповідні додаткові обчислення. При h = 1/16 = 0,0625 отримуємо:

	N	O	P
	х	f (x)	к
	0,0625	0,066488
	0,125	0,141275
	0,1875	0,224845
	0,25	0,317673
	0,3125	0,420219
	0,375	0,532923
	0,4375	0,656203
	0,5	0,790439
	0,5625	0,935975
	0,625	1,093106
	0,6875	1,262067
	0,75	1,443029
	0,8125	1,636086
	0,875	1,841241
	0,9375	2,0584
		2,287355

Додамо отримані дані у попередню таблицю кратного перерахунку. Маємо:

	A	B	C	D	E	F
	№ перерахунку
	n	s	I	R	I	R
		5,449112	0,908185
		10,91104	0,909254	7,12176E-05	0,909325
		21,82382	0,909326	4,81561E-06	0,909331	1,88137E-07
		43,64786	0,90933	3,0651E-07	0,909331	2,85653E-09

Отже, нарешті ми отримали оцінку похибки належного порядку у чарунці F19, задача розв’язана. Це оцінка похибки наближеного значення інтегралу, що міститься у чарунці Е19 і ≈ 0,909330672 (таке значення було отримане після розширення стовпця цієї чарунки в Excel). Насправді отриманий порядок знову більший на одиницю гарантованого методом кратного перерахунку. Ми можемо тепер провести ще третій перерахунок і подивитись на порядок третього уточненого значення:

	A	B	C	D	E	F	G	H
	№ перерахунку
	n	s	I	R	I	R	I	R
		*	*
		*	↓	*	*
		*	↓	↓	↓	*	= E18 + F18
		*	↓	↓	↓	↓	↓	= 1/63*(G19 – G18)

Тут р = 6, 2^р – 1 = 63. В результаті дістаємо:

	A	B	E	F	G	H
	№ перерахунку
	n	s	I	R	I	R
		5,449112
		10,91104	0,909325
		21,82382	0,909331	1,88137E-07	0,909331
		43,64786	0,909331	2,85653E-09	0,909331	-1,53536E-09

Порядок похибки третього уточненого значення не зріс: насправді можна довести, що при зростанні порядку у деякому перерахунку вище гарантованого у наступному перерахунку зростання у наступному, як правило, не відбудеться.

Дата добавления: 2014-10-31