Переход к параметрическим и каноническим уравнениям прямой в пространстве

Бывают случаи, в которых использование уравнений двух пересекающихся плоскостей для описания прямой не совсем удобно. Некоторые задачи проще решаются, если известны канонические уравнения прямой в пространстве вида 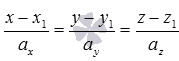или параметрические уравнения прямой в пространстве вида 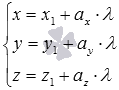, где x₁, y₁, z₁ - координаты некоторой точки прямой, a_x, a_y, a_z - координаты направляющего вектора прямой, а 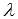- параметр, принимающий произвольные действительные значения. Опишем процесс перехода от уравнений прямой вида к каноническим и параметрическим уравнениям прямой в пространстве.

В предыдущих пунктах мы научились находить координаты некоторой точки прямой, а также координаты некоторого направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей. Этих данных достаточно, чтобы записать и канонические и параметрические уравнения этой прямой в прямоугольной системе координат в пространстве.

Рассмотрим решение примера, а после этого покажем еще один способ нахождения канонических и параметрических уравнений прямой в пространстве.

Пример. Прямая в трехмерном пространстве задана уравнениями двух пересекающихся плоскостей 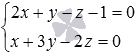. Напишите канонические и параметрические уравнения этой прямой.

Решение. Вычислим сначала координаты направляющего вектора прямой. Для этого найдем векторное произведение нормальных векторов 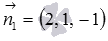и плоскосте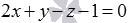й и :

То есть, .

Теперь определим координаты некоторой точки заданной прямой. Для этого найдем одно из решений системы уравнений .

Определитель отличен от нуля, возьмем его в качестве базисного минора основной матрицы системы. Тогда переменная z является свободной, переносим слагаемые с ней в правые части уравнений, и придаем переменной z произвольное значение :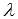

Решаем методом Крамера полученную систему уравнений:

Следовательно,

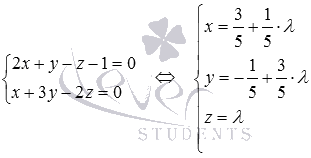
Примем , при этом получаем координаты точки прямой: .

Теперь мы можем записать требуемые канонические и параметрические уравнения исходной прямой в пространстве:

Ответ. и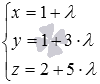

Вот второй способ решения этой задачи.

При нахождении координат некоторой точки прямой мы решаем систему уравнений . В общем случае ее решения можно записать в виде .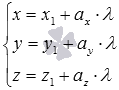

А это как раз искомые параметрические уравнения прямой в пространстве. Если каждое из полученных уравнений разрешить относительно параметра 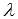и после этого приравнять правые части равенств, то получим канонические уравнения прямой в пространстве

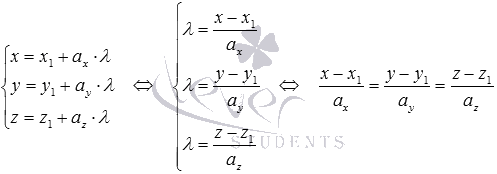
Покажем решение предыдущей задачи по этому методу.

Пример. Прямая в трехмерном пространстве задана уравнениями двух пересекающихся плоскостей 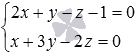. Напишите канонические и параметрические уравнения этой прямой.

Решение. Решаем данную систему из двух уравнений с тремя неизвестными (решение приведено в предыдущем примере, не будем повторяться). При этом получаем 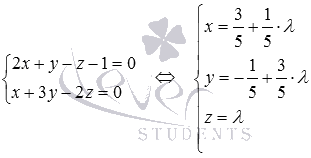. Это и есть искомые параметрические уравнения прямой в пространстве.

Осталось получить канонические уравнения прямой в пространстве:

Полученные уравнения прямой внешне отличаются от уравнений, полученных в предыдущем примере, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства (а значит, одну и ту же прямую).

Ответ. и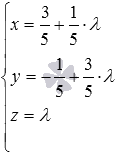

Дата добавления: 2014-10-31