
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Главный определитель системы и определители неизвестных. Теорема Крамера
|
|
|
|
Ответ:.Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается  (дельта).
(дельта).
Определители 
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
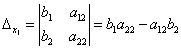 ;
;
 .
.
Формулы Крамера для нахождения неизвестных:
 .
.
Найти значения  и
и  возможно только при условии, если
возможно только при условии, если
 .
.
Этот вывод следует из следующей теоремы.
Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
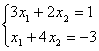 . (2)
. (2)
Согласно теореме Крамера имеем:

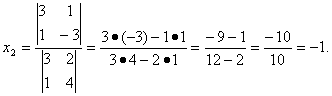

Итак, решение системы (2):
9.операции над множествами. диаграммы Вьена.
Ответ:
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
|
|
|
Операции над множествами рассматриваются для получения новых множеств из уже существующих.
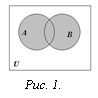 Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
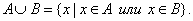
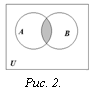 Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

Ответ: -
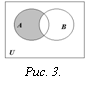 Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

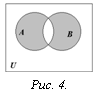 Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
11.отображения (функция), область определения, образы множеств при отображении, множество значений функции и её график.
Ответ: Отображением множества E в множество F, или функцией, определенной на E со значениями в F, называется правило, или закон f, который каждому элементу 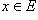 ставит в соответствие определенный элемент
ставит в соответствие определенный элемент  .
.
Элемент 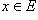 называют независимым элементом, или аргументом функции f, элемент
называют независимым элементом, или аргументом функции f, элемент  называют значением функции f, илиобразом; при этом элемент
называют значением функции f, илиобразом; при этом элемент 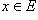 называется прообразом элемента
называется прообразом элемента  .
.
Отображение (функцию) обычно обозначают буквой f или символом 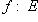
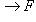 , указывая тем самым, что f отображает множество E в F. Употребляется также обозначение
, указывая тем самым, что f отображает множество E в F. Употребляется также обозначение 
 , указывающее, что элементу x соответствует элемент f(x). Иногда функцию удобно задавать посредством равенства, в котором содержится закон соответствия. Например, можно говорить, что "функция f определена равенством
, указывающее, что элементу x соответствует элемент f(x). Иногда функцию удобно задавать посредством равенства, в котором содержится закон соответствия. Например, можно говорить, что "функция f определена равенством 

 ". Если "y" - общее наименование элементов множества F, т. е. F = {y}, то отображение
". Если "y" - общее наименование элементов множества F, т. е. F = {y}, то отображение 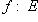
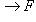 записывают в виде равенстваy = f(x) и говорят, что это отображение задано явно.
записывают в виде равенстваy = f(x) и говорят, что это отображение задано явно.
|
|
|
2. Образ и прообраз множества при заданном отображении
Пусть задано отображение 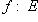
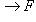 и множество
и множество 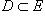 .
.
Множество элементов из F, каждый из которых является образом хотя бы одного элемента из D при отображении f, называется образоммножества D и обозначается f(D).
Очевидно, 

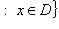 .
.
Пусть теперь задано множество 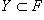 .
.
Множество элементов 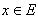 таких, что
таких, что 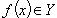 , называется прообразом множества Y при отображении f и обозначается f -1(Y).
, называется прообразом множества Y при отображении f и обозначается f -1(Y).
Если  , то
, то 
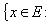
 . Если при каждом
. Если при каждом  множество f -1(y) состоит не более чем из одного элемента
множество f -1(y) состоит не более чем из одного элемента 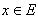 , то f называетсявзаимно однозначным отображением E в F. Впрочем, можно определить взаимно однозначное отображение f множества E на F.
, то f называетсявзаимно однозначным отображением E в F. Впрочем, можно определить взаимно однозначное отображение f множества E на F.
Отображение 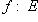
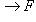 называется:
называется:
- инъективным (или инъекцией, или взаимно однозначным отображением множества E в F), если 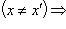
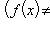
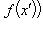 , или если
, или если  уравнение f(x) = y имеет не более одного решения;
уравнение f(x) = y имеет не более одного решения;
- сюръективным (или сюръекцией, или отображением множества E на F), если f(E) = F и если  уравнение f(x) = y имеет по крайней мере одно решение;
уравнение f(x) = y имеет по крайней мере одно решение;
- биективным (или биекцией, или взаимно однозначным отображением множества E на F), если оно инъективно и сюръективно, или если  уравнение f(x) = y имеет одно и только одно решение.
уравнение f(x) = y имеет одно и только одно решение.
3. Суперпозиция отображений. Обратное, параметрическое и неявное отображения
1) Пусть 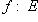
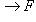 и
и 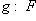
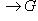 . Поскольку
. Поскольку 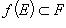 , то отображение g каждому элементу
, то отображение g каждому элементу 
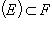 относит определенный элемент
относит определенный элемент 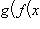
 .
.
Таким образом, каждому 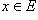 посредством правила
посредством правила  поставлен в соответствие элемент
поставлен в соответствие элемент

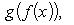

Тем самым определено новое отображение (или новая функция), которое назовем композицией отображений, или суперпозицией отображений, или сложным отображением.
2) Пусть 
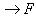 - биективное отображение и F = {y}. В силу биективности f каждому
- биективное отображение и F = {y}. В силу биективности f каждому  соответствует единичный образ x, который обозначим через f -1(y), и такой, что f(x) = y. Таким образом, определено отображение
соответствует единичный образ x, который обозначим через f -1(y), и такой, что f(x) = y. Таким образом, определено отображение 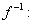
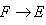 , которое называется обратным отображению f, или обратной функцией функции f.
, которое называется обратным отображению f, или обратной функцией функции f.
Очевидно, отображение f обратно отображению f -1. Поэтому отображения f и f -1 называют взаимно обратными. Для них справедливы соотношения

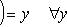

3) Пусть

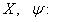
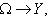
причем хотя бы одно из этих отображений, например 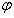 , биективно. Тогда существует обратное отображение
, биективно. Тогда существует обратное отображение 
 , а значит,
, а значит, 
 .
.
Определенное таким образом отображение называется заданным параметрически с помощью отображений 

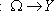 ; причем переменная из
; причем переменная из 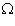 называется параметром.
называется параметром.
|
|
|
4) Пусть на множестве 
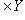 определено отображение
определено отображение 
 , где множество
, где множество 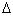 содержит нулевой элемент. Предположим, что существуют множества
содержит нулевой элемент. Предположим, что существуют множества 

 такие, что при каждом фиксированном
такие, что при каждом фиксированном 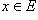 уравнение
уравнение 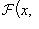
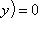 имеет единственное решение
имеет единственное решение 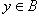 . Тогда на множестве E можно определить отображение
. Тогда на множестве E можно определить отображение 
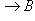 , ставящее каждому
, ставящее каждому 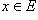 в соответствие то значение
в соответствие то значение 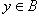 , которое при указанном x является решением уравнения
, которое при указанном x является решением уравнения 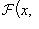
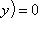 .
.
Относительно так определенного отображения

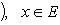

говорят, что оно задано неявно посредством уравнения 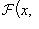
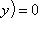 .
.
5) Отображение 
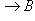 называется продолжением отображения
называется продолжением отображения 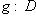
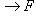 , а g - сужением отображения f, если
, а g - сужением отображения f, если 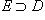 и
и 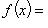
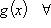
 .
.
Сужение отображения 
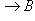 на множество
на множество 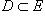 иногда обозначают символом
иногда обозначают символом 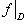 .
.
6) Графиком отображения 
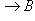 называется множество
называется множество

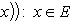
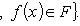
Ясно, что 
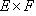 .
.
12. монотонные функции. Обратная функция, теорема существования. Функции y=arcsinx y=arcos x х свойства и графики.
Ответ: Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю то функция называется стро́го моното́нной.
.Пусть имеется функция f(x) определенная на отрезке <a,b>, значения которой принадлежат некоторому отрезку <c,d>. Если
,
то говорят, что на отрезке <c,d> определена функция, обратная к функции f(x) и обозначают это так:x=f(-1)(y).
Обратите внимание на отличие этого определения от определения заполненности отрезка <c,d> сплошь. В определении f(-1)(…) стоит квантор, т.е. значение х, обеспечивающее равенство y=f(x), должно быть единственным, в то время как в определении заполненности отрезка<c,d> сплошь стоит квантор, что говорит о том, что может быть несколько значений х, удовлетворяющих равенству y=f(x).
Обычно, говоря об обратной функции, заменяют х на у а y на x(x «y) и пишут y=f(-1)(x). Очевидно, что исходная функция f(x) и обратная функция f(-1)(x) удовлетворяют соотношению
f(-1)(f(x))=f(f(-1)(x))=x.
Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.
|
|
|
Теорема. Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке [a,b]. Тогда на отрезке [f(a),f(b)] определена обратная функция f(-1)(x), которая также непрерывна и строго монотонно возрастает (убывает).
Доказательство.
Докажем теорему для случая, когда f(x) строго монотонно возрастает.
1. Существование обратной функции.
Так как по условию теоремы f(x) непрерывна, то, согласно предыдущей теореме, отрезок [f(a),f(b)] заполнен сплошь. Это означает, что.
Докажем, что х единственно. Действительно, если взять х’>x, то будет f(x’)>f(x)=y и поэтому f(x’)>y. Если взять х’’<x, то будет f(x’’)<f(x)=y и поэтому f(x’’)<y. В обоих случаях f(x)¹ y и поэтому x единственно. Следовательно, х=f(-1)(y) и f(-1)(…) существует.
2. Монотонность обратной функции.
Сделаем обычную замены x «y и будем писать y= f(-1)(x). Это значит, что x=f(y).
Пусть x1>x2. Тогда:
y1= f(-1)(x1); x1=f(y1)
y2= f(-1)(x2); x2=f(y2)
Какое же соотношение между y1 и y2? Проверим возможные варианты.
а) y1<y2? Но тогда f(y1)<f(y2) и x1<x2, а у нас было x1>x2.
б) y1=y2? Но тогда f(y1)=f(y2) и x1=x2, а у нас было x1>x2.
в) Остается единственный вариант y1>y2, т.е. Но тогда f(-1)(x1)>f(-1)(x2), а это и означает, что f(-1)(…) строго монотонно возрастает.
3. Непрерывность обратной функции.
Т.к. значения обратной функции заполняют сплошь отрезок [a,b], то по предыдущей теоремеf(-1)(…) непрерывна. <
<="" a="" style="color: rgb(255, 68, 0);">
| y = arcsin x | y = arccos x |
функция обратная функции y = sin x, - / 2 / 2  x x   / 2 / 2
| функция обратная функции y = cos x, 0  x x  
|

| 
|
<="" a="" style="color: rgb(0, 0, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">
Свойства функций
| y = arcsin x | y = arccos x | ||
| ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: | [-1; 1] | [-1; 1] | |
| ОБЛАСТЬ ЗНАЧЕНИЙ: | 
| [0;  ) )
| |
| ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: | нечетная | ни четная, ни нечетная | |
| НУЛИ: | y = 0 при x = 0 | y = 0 при x = 1 | |
| ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА: | y > 0, при x  (0; (0; 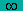 ] y < 0, при x ] y < 0, при x  [-1; 0) [-1; 0)
| y = 0 при x = 1 y > 0 при x  [-1; 1) [-1; 1)
| |
| ЭКСТРЕМУМЫ: | нет | нет | |
| ПРОМЕЖУТКИ МОНОТОННОСТИ: | возрастает на всей области определения | убывает на всей области определения |
arcsin x + arccos x =  /2
/2
<="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">
| y = arctg x | y = arcctg x |
функция обратная функции y = tg x, - / 2 < x < / 2 < x <  / 2 / 2
| функция обратная функции y = ctg x, 0 < x < 
|
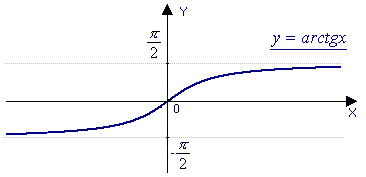
13.композиция функций. Элементарные функции. Функции y=arctg x, y = arcctg x, их свойства и графики.
Ответ: В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой.
Композиция функций G и F обычно обозначается G∘F, что обозначает применение функции G к результату функции F.
Пусть F:X→Y и G:F(X)⊂Y→Z две функции. Тогда их композицией называется функция G∘F:X→Z, определённая равенством:
(G∘F)(x)=G(F(x)),x∈X.
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций[1]:
- алгебраические:
- степенная;
- рациональная.
- трансцендентные:
- показательная и логарифмическая;
- тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
<="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">
| y = arctg x | y = arcctg x |
функция обратная функции y = tg x, - / 2 < x < / 2 < x <  / 2 / 2
| функция обратная функции y = ctg x, 0 < x < 
|
| 
|
| y = arctg x | y = arcctg x | |
| ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: | R | R |
| ОБЛАСТЬ ЗНАЧЕНИЙ: | 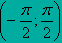
| (0;  ) )
|
| ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: | нечетная | ни четная, ни нечетная |
| НУЛИ: | y = 0 при x = 0 | нулей нет |
| ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА: | y > 0, при x  (0; (0; 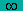 ] y < 0, при x ] y < 0, при x  (- (- ; 0) ; 0)
| y > 0 при x  R R
|
| ЭКСТРЕМУМЫ: | нет | нет |
| ПРОМЕЖУТКИ МОНОТОННОСТИ: | возрастает при x  R R
| убывает при x  R R
|
arctg x + arcctg x =  /2
/2
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 4707; Нарушение авторских прав?; Мы поможем в написании вашей работы!