Бесконечно- малые величины и их свойства. Теорема о структуре сходящейся прямой

Ответ: БЕСКОНЕЧНО МАЛЫЕ И ИХ СВОЙСТВА

Функция α(х) называется бесконечно малой при , если ,

т. е. для любого числа ε > 0 существует такое число δ > 0, что для всех х, удовлетворяющих неравенству

,

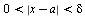выполняется неравенство

.

Бесконечно малую функцию α(х) называют бесконечно малой величиной или просто бесконечно малой.

Функция f (х) называется ограниченной при , если существуют положительные числа М и δ, такие, что при условии
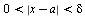, выполняется неравенство
.

Например, любая бесконечно малая α(х) является ограниченной функцией при .

В дальнейшем будем рассматривать бесконечно малые при .

Свойства бесконечно малых.

1. Если функци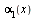и и являются бесконечно малыми, то функция 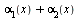также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.

2. Произведение ограниченной при функции на бесконечно малую есть функция бесконечно малая.

3. Произведение постоянной на бесконечно малую есть бесконечно малая.

4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.

Последовательность, у которой существует предел, называется сходящейся.

ТЕОРЕМА: Сходящаяся последовательность имеет только один предел.

Доказательство: Пусть a и b – пределы сходящейся последовательности {x_n}. Тогда, используя специальное представление для элементов x_n сходящейся последовательности {x_n}, получим x_n=а+a_n, x_n=b+b_n, где a_n и b_n– элементы бесконечно малых последовательностей {a_n} и {b_n}.

Вычитая данные соотношения, найдем a_n-b_n=b-a. Так как все элементы бесконечно малой последовательности {a_n-b_n} имеют одно и то же постоянное значение b-a, то (по теореме: Если все элементы бесконечно малой последовательности {a_n} равны одному и тому же числу с, то с=0) b-a=0, т.е. b=a. Теорема доказана.

ТЕОРЕМА: Сходящаяся последовательность ограничена.

Доказательство: Пусть {x_n} - сходящаяся последовательность и а – ее предел. Представим ее в следующем виде:

x_n=а+a_n,

где a_n- элемент бесконечно малой последовательности. Так как бесконечно малая последовательность {a_n} ограничена (по теореме: Бесконечно малая последовательность ограничена.), то найдется такое число А, что для всех номеров n справедливо неравенство |a_n|£А. Поэтому | x_n | £ |a| + A для всех номеров n, что и означает ограниченность последовательности {x_n}. Теорема доказана.

Ограниченная последовательность может и не быть сходящейся. Например, последовательность 1, -1, 1, -1, … - ограничена, но не является сходящейся. В самом деле, если бы эта последовательность сходилась к некоторому числу а, то каждая из последовательностей {x_n-a} и {x_n+1-a} являлась бы бесконечно малой. Но тогда (по теореме: Разность бесконечно малых последовательностей есть бесконечно малая последовательность.) {(x_n-a) – (x_n+1-a)}={x_n– x_n+1} была бы бесконечно малой, что невозможно т.к. |x_n– x_n+1| = 2 для любого номера n.

ТЕОРЕМА: Сумма сходящихся последовательностей {х_n} и {y_n} есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей {х_n} и {y_n}.

Доказательство: Пусть а и b – соответственно пределы последовательностей {х_n} и {y_n}. Тогда:

x_n=а+a_n, y_n=b+b_n,

где {a_n} и {b_n) – бесконечно малые последовательности. Следовательно, (х_n + y_n) - (а + b) =a_n+b_n.

Таким образом, последовательность {(х_n + y_n) - (а + b)} бесконечно малая, и поэтому последователдьность {х_n + y_n} сходится и имеет своим пределом число а+b. Теорема доказана.

Дата добавления: 2014-10-31