Односторонние пределы, теорема, примеры

Пусть на некотором числовом множестве M ∈R задана числовая функция f: M →R и число a — предельная точка области определения M. Существуют различные определения для односторонних пределов функции f (x) в точке a, но все они эквивалентны.

Односторонний предел по Гейне [править | править вики-текст]

· Число A ∈R называется правосторонним пределом (правым пределом, пределом справа) функции f (x) в точке a, если для всякой последовательности { xn }∞ n =1, состоящей из точек, больших числа a, которая сама сходится к числу a, соответствующая последовательность значений функции { f (xn)}∞ n =1сходится к числу A.

lim x → a +0 f (x)= A ⇔∀{ xn }∞ n =1:(∀ k ∈N: xk > a)∧lim n →∞ xn = a ⇒lim n →∞{ f (xn)}∞ n =1= A

· Число A ∈R называется левосторонним пределом (левым пределом, пределом слева) функции f (x) в точке a, если для всякой последовательности { xn }∞ n =1, состоящей из точек, меньших числа a, которая сама сходится к числу a, соответствующая последовательность значений функции { f (xn)}∞ n =1сходится к числу A. ^[1]

lim x → a −0 f (x)= A ⇔∀{ xn }∞ n =1:(∀ k ∈N: xk < a)∧lim n →∞ xn = a ⇒lim n →∞{ f (xn)}∞ n =1= A

Односторонний предел по Коши [править | править вики-текст]

· Число A ∈R называется правосторонним пределом (правым пределом, пределом справа) функции f (x) в точке a, если для всякого положительного числа ε отыщется отвечающее ему положительное число δ такое, что для всех точек x из интервала (a, a + δ) справедливо неравенство | f (x)− A |< ε.

lim x → a +0 f (x)= A ⇔∀ ε >0 ∃ δ = δ (ε)>0 ∀ x ∈(a, a + δ):| f (x)− A |< ε

· Число A ∈R называется левосторонним пределом (левым пределом, пределом слева) функции f (x) в точке a, если для всякого положительного числа ε отыщется отвечающее ему положительное число δ, такое, что для всех точек x из интервала (a − δ, a) справедливо неравенство | f (x)− A |< ε. ^[1]

lim x → a −0 f (x)= A ⇔∀ ε >0 ∃ δ = δ (ε)>0 ∀ x ∈(a − δ, a):| f (x)− A |< ε

Односторонний предел как предел вдоль фильтра [править | править вики-текст]

Односторонний предел является частным случаем общего понятия предела функции вдоль фильтра. Пусть M ⊂R, и a ∈ M ′. Тогда системы множеств

B+={(a, a + δ)∩ M ∣ δ >0}

и

B−={(a − δ, a)∩ M ∣ δ >0}

являются фильтрами. Пределы вдоль этих фильтров совпадают с соответствующими односторонними пределами:

limB+ f (x)≡lim x → a + f (x);

limB− f (x)≡lim x → a − f (x).

Обозначения[править | править вики-текст]

· Правосторонний предел принято обозначать любым из нижеследующих способов:

lim x → a + f (x), lim x → a +0 f (x), lim x ↓ af (x), lim x ↘ af (x);

· Аналогичным образом для левосторонних пределов приняты обозначения:

lim x → a − f (x), lim x → a −0 f (x), lim x ↑ af (x), lim x ↗ af (x).

· При этом используются также сокращённые обозначения:

· f (a +) и f (a +0) для правого предела;

· f (a −) и f (a −0) для левого предела.

Свойства[править | править вики-текст]

· Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра.

· Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.^[1]

Примеры[править | править вики-текст]

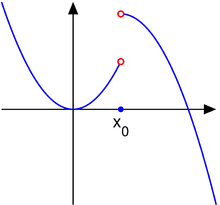
Функция из второго примера

· Тождественная числовая функция

· f (x)= x

· Область определения: R

· Правый предел: ∀ a ∈R:lim x → a +0 x = a

· Левый предел: ∀ a ∈R:lim x → a −0 x = a

· Правый и левый пределы совпадают, так что имеется обычный предел: ∀ a ∈R:lim x → ax = a

· Кусочно-заданная функция

· f (x)={ x 2,11−(x −3)2, x <3 x >3

· Область определения: R∖{3}

· Правый предел: lim x →3+0 f (x)=11

· Левый предел: lim x →3−0 f (x)=9

· Правый и левый пределы различны, так что обычного предела в точке x =3 не существует

· Функция sgn(x)

· f (x)={0, x ∣∣ x ∣∣, x =0 x ≠0

· Область определения: R

· Правый предел: lim x →0+0sgn(x)=+1

· Левый предел: lim x →0−0sgn(x)=−1

· Правый и левый пределы различны, так что обычного предела в точке x =0 не существует

Дата добавления: 2014-10-31