Алгоритм симплексного метода

Общая постановка задачи

Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования, за­писанную в каноническом виде.

Идея симплексного метода (метода последовательного улуч­шения плана) заключается в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по опорным решениям задачи к оп­тимальному. Значение целевой функции при этом перемеще­нии для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оп­тимальное опорное решение. Опорным решением называется базисное неотрицательное решение.

1. Математическая модель задачи должна быть канонической. Если она неканоническая, то ее надо привести к каноническому виду.

2. Находим исходное опорное решение и проверяем его на оптимальность. Для этого заполняем симплексную таблицу (табл. 21.1). Все строки таблицы 1-го шага, за исключением строки Δ _j (индексная строка), заполняем по данным системы ограничений и целевой функции.

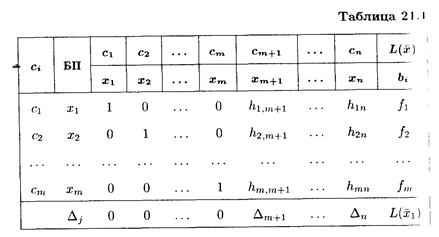
Индексная строка для переменных находится по формуле

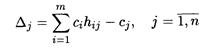
и по формуле

Возможны следующие случаи при решении задачи на максимум:

— если все оценки Δ _j ≥ 0, то найденное решение оптимальное;

— если хотя бы одна оценка Δ _j ≤ 0, но при соответствующей переменной нет ни одного положительного коэффициента, решение задачи прекращаем, так как L() → , т.е. целевая функция неограничена в области допусти­мых решений;

— если хотя бы одна оценка отрицательная, а при соответ­ствующей переменной есть хотя бы один положитель­ный коэффициент, то нужно перейти к другому опорно­му решению;

— если отрицательных оценок в индексной строке несколь­ко, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по аб­солютной величине отрицательная оценка.

Если хотя бы одна оценка Δ _k < 0, то k- й столбец прини­маем за ключевой. За ключевую строку принимаем ту, кото­рой соответствует минимальное отношение свободных членов (b_i) к положительным коэффициентам k- гo столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называется ключевым элементом.

3. Заполняем симплексную таблицу 2-го шага:

— переписываем ключевую строку, разделив ее на ключе­вой элемент;

— заполняем базисные столбцы;

— остальные коэффициенты таблицы находим по прави­лу "прямоугольника"*. Оценки можно считать по приве­денным выше формулам или по правилу "прямоугольни­ка" Получаем новое опорное решение, которое проверяем на оптимальность, и т.д.

* Правило "прямоугольника" заключается в следующем. Пусть ключе­вым элементом 1-го шага является элемент 1-й строки (m + 1)-го столбца h _{1, m+ 1}. Тогда элемент i -й строки (m + 2)-го столбца 2-го шага — обозначим его h’_{i,m +2} — согласно правилу "прямоугольника" выражается формулой

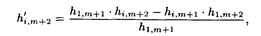
где h_{i , m+ 2}, h_{i , m+ 1}, h _{1, m+ 1}— элементы 1-го шага.

Примечание. Если целевая функция L() требует нахож­дения минимального значения, то критерием оптимальности задачи является неположительность оценок Δ _j при всех j =.

Дата добавления: 2014-10-15