Параметри шрифтів 7 страница

СПРЯЖЕННЯ ЛІНІЙ

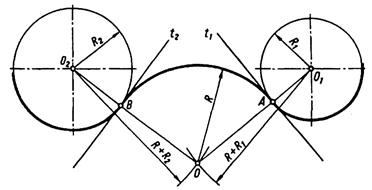Рисунок 44. Зовнішнє спряження.

Рисунок 45. Внутрішнє спряження.

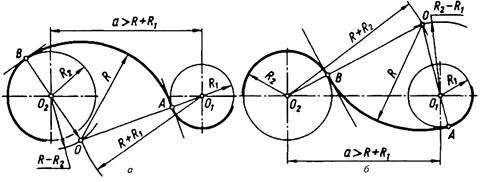Рисунок 46. Змішане спряження.

ПОБУДОВА КОРОБОВИХ КРИВИХ

Коробовими називаються опуклі криві, утворені спряженням дуг кіл. До коробових кривих належать овали, овоїди, завитки тощо.

Овал – це замкнена коробова крива, яка має дві осі симетрії.

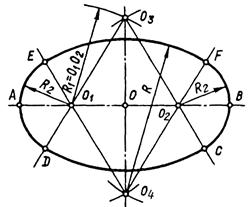
Рисунок 47. Побудова овалу.

Рисунок 48. Побудова овалу.

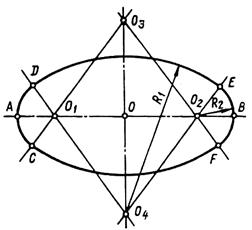Рисунок 49. Побудова овалу.

ПОБУДОВА КОРОБОВИХ КРИВИХ

Овоїд - це овал, що має одну вісь симетрії (рис. 50).

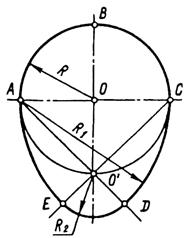Рисунок 50. Побудова овоїду.

Завиток - це плоска спіральна крива, яка викреслюється циркулем шляхом спряження дуг кіл. Вони бувають дво -, три -, чотири - та багато центрові.

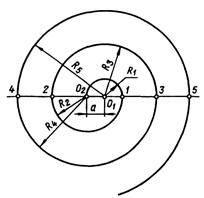Рисунок 51. Побудова завитка.

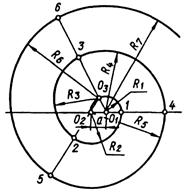Рисунок 52. Побудова завитка.

ЛЕКАЛЬНІ КРИВІ

Лекальними називаються криві, які креслять за допомогою лекал за попередньо знайденими точками. До лекальних кривих належать еліпс, парабола, гіпербола, синусоїда, циклоїда, епіциклоїда, гіпоциклоїда тощо.

Рисунок 53. Побудова плоскої лекальної кривої (точки лежать в одній площині).

Криві другого порядку

Криві другого порядку утворюються внаслідок перетину прямого колового конуса площиною; в перерізах отримують еліпс, параболу або гіперболу.

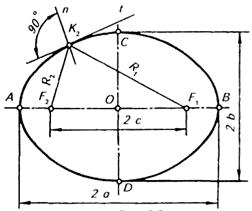
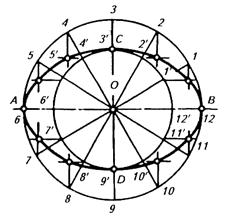
Еліпсом називається замкнена плоска крива, що виявляє собою геометричне місце точок К, для яких сума відстаней R₁ і R₂ до двох заданих точок F₁ і F₂ (фокусів) є стала величина, що дорівнює великий осі еліпса, тобто R₁ + R₂ = АВ (рис.54, 55).

Рисунок 54. Побудова еліпса. Рисунок 55. Побудова еліпса.

ЛЕКАЛЬНІ КРИВІ

Криві другого порядку

Гіперболою називається незамкнена плоска крива, різниця відстаней будь-якої точки К від фокусів F₁ і F₂ якої – стала величина, що дорівнює відстані між вершинами гіперболи, тобто F₂ K – F₁ K = A₁A₂ (рис.56, 57).

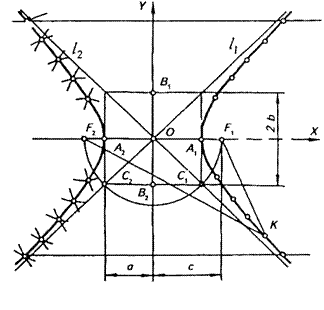Рисунок 56. Побудова гіперболи.

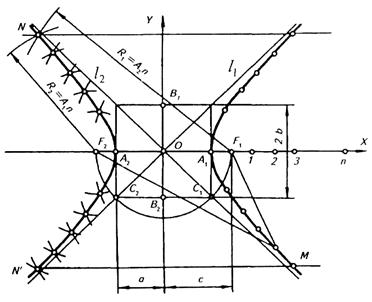Рисунок 57. Побудова гіперболи.

ЛЕКАЛЬНІ КРИВІ

Криві другого порядку

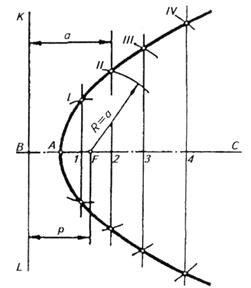
Параболою називається незамкнена плоска крива, кожна точка якої однаково віддалена від напрямної прямої (директриси) вершинами гіперболи, тобто KL і від фокуса F (рис.58, 59).

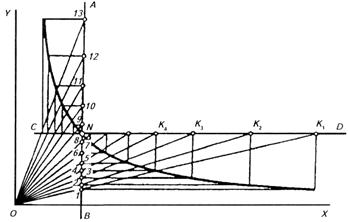Рисунок 58. Побудова параболи.

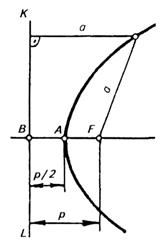а б

Рисунок 59, а, б. Побудова параболи.

ЛЕКАЛЬНІ КРИВІ

Спіральні криві

Спіраль Архімеда - плоска крива, яку описує точка, що рівномірно рухається по радіусу кола, яке рівномірно обертається в площині навколо нерухомої точки.

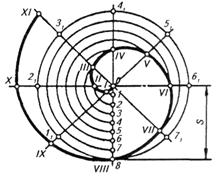Рисунок 60. Побудова спіралі Архімеда.

Евольвентою кола називається плоска крива, яка утворюється точкою прямої лінії, що котиться без ковзання по нерухомому колу заданого радіуса.

Рисунок 61. Побудова евольвенти кола.

Синусоїда -плоска крива, яка виражає закон зміни синуса залежно від зміни величини кута (рис.62).

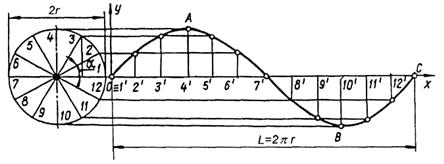Рисунок 62. Побудова синусоїди.

ЛЕКАЛЬНІ КРИВІ

Циклічні криві

Циклічні криві являють собою плоскі криві, які описуються точками кіл, що котяться без ковзання. До циклічних кривих належать циклоїда, епіциклоїда, гіпоциклоїда.

Циклоїдою називається плоска крива (рис.63), яку описує точка кола, яке котиться без ковзання по напрямній прямій.

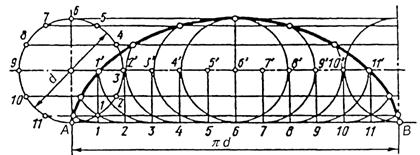Рисунок 63. Побудова циклоїди.

Епіциклоїдою називається плоска крива (рис.64), яка описується точкою твірного (рухомого) кола, що котиться без ковзання ззовні по нерухомому напрямному колу.

Рисунок 64. Побудова епіциклоїди.

ЛЕКАЛЬНІ КРИВІ

Циклічні криві

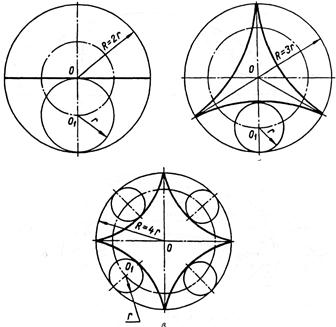
Гіпоциклоїдою називається плоска крива, яка описується точкою твірного (рухомого) кола, що котиться без ковзання зсередини нерухомого напрямного кола (рис.65).

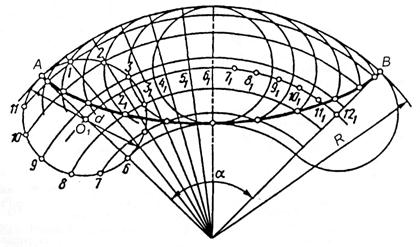Рисунок 65. Побудова гіпоциклоїди

Рисунок 66. Побудова гіпоциклоїди.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Будь-яку плоску чи просторову фігуру можна розглядати як сукупність точок, ліній та поверхонь. Така фігура називається оригіналом.

Властивості оригіналу можна вивчити за певними правилами, тобто якщо є однозначна відповідність між геометричними властивостями оригіналу та його рисунка. Для побудови зображень оригіналу користуються методом проекцій.

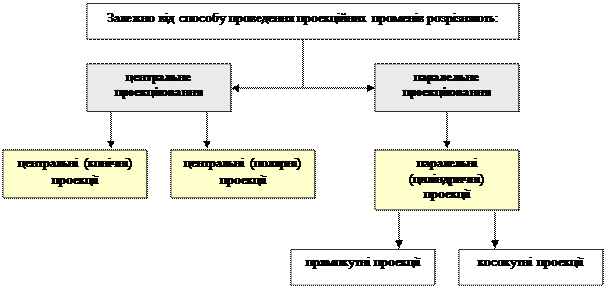Якщо проекційні промені перпендикулярні до площини проекцій, то такий спосіб проекціювання називається прямокутним, а проекції – прямокутними.

Усі інші проекції – косокутні.

При побудові креслень використовується прямокутне проекціювання на одну, дві або три взаємно перпендикулярні площини.

Одна прямокутна проекція точки не визначає її положення в просторі.

Рисунок 67. Центральне проекціювання. Рисунок 68. Паралельне проекціювання.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

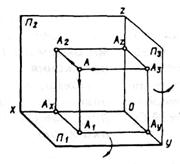Рисунок 69, а. Проекціювання точки на три площини проекцій.

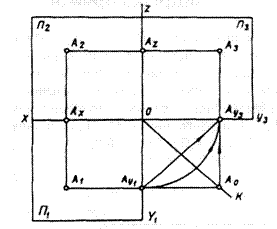Рисунок 69, б. Комплексне креслення.

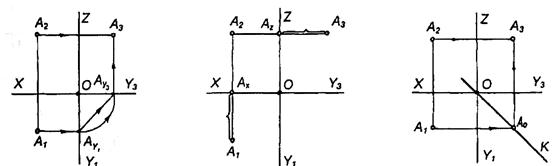Рисунок 70, а, б, в. Побудова третьої проекції точки за двома відомими її проекціями.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Рисунок 71, а. Три проекції відрізка прямої.

Рисунок 71, б. Комплексне креслення.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Прямі окремого (особливого, часткового) положення – це прямі, які паралельні або перпендикулярні до площин проекцій.

Пряма рівня – це пряма, яка паралельна площині проекцій.

Проекційна пряма – це пряма, яка перпендикулярна до площини проекцій.

	Профільні прямі, паралельні П3
		Профільно-проекційні, що перпендикулярні до профільної площини проекцій

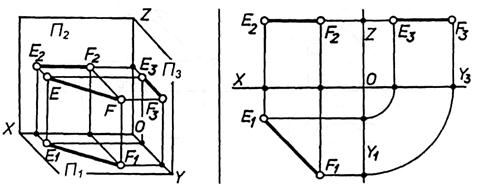Рисунок 72. Розташування прямої відносно площин проекцій.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Рисунок 73. Розташування прямої відносно площин проекцій.

Рисунок 74. Розташування прямої відносно площин проекцій.

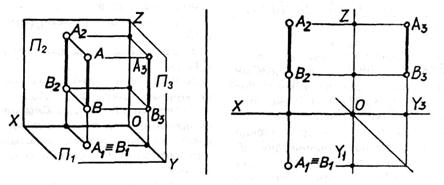Рисунок 75. Розташування прямої відносно площин проекцій.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Рисунок 76. Розташування прямої відносно площин проекцій.

Рисунок 77. Розташування прямої відносно площин проекцій.

Рисунок 78. Розташування прямої відносно площин проекцій.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Щоб навчитись читати креслення і будувати зображення складних технічних форм, треба вміти аналізувати різні положення площини в просторі.

На комплексному кресленні площина може бути задана:

1. трьома точками, що не лежать на одній прямій;

2. прямою і точкою, що не належать цій прямій;

3. двома перетин ними прямими;

4. двома паралельними прямими;

5. плоскою фігурою (трикутником, чотирикутником, колом);

6. слідами.

Слід площини – це пряма, по якій площина перетинає площину проекцій.

Сліди позначаються так: h⁰ - горизонтальний; f⁰ - фронтальний; p⁰ - профільний.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

Рисунок 79, 80. Положення площини відносно площин проекцій.

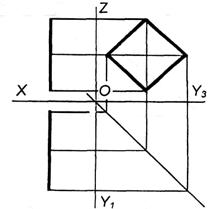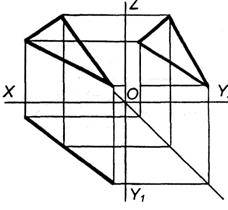Рисунок 81, 82. Положення площини відносно площин проекцій.

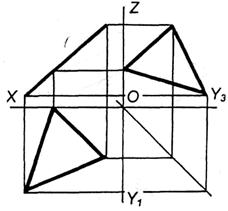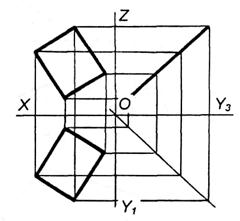
Рисунок 83, 84. Положення площини відносно площин проекцій.

МЕТОД ПРОЕКЦІЮВАННЯ

Проекціювання точки, прямої, площини

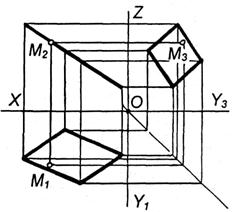Рисунок 85, 86. Положення площини відносно площин проекцій.

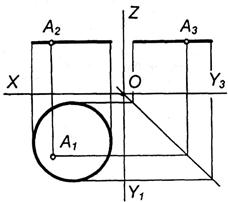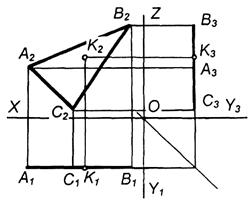
Рисунок 87, 88. Положення площини відносно площин проекцій.

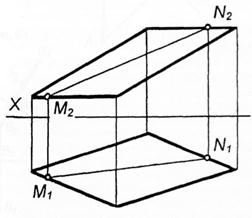
Рисунок 89, 90. Положення площини відносно площин проекцій.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Поняття про переріз геометричних тіл

Деталь будь-якої форми можна уявити як сукупність окремих геометричних тіл. Такими тілами, зокрема, є багатогранники та тіла обертання.

Багатогранниками називаються геометричні тіла, обмежені плоскими багатокутниками. Ці багатокутники називаються гранями. Лінії перетину граней називаються ребрами. Точки перетину ребер називаються вершинами.

Переріз призми площиною

Призмою називається багатогранник, дві грані (основи) якого – рівні багатокутники з відповідно паралельними сторонами, а бічні грані в загальному випадку – паралелограми.

Призма є прямою, якщо бічні ребра перпендикулярні до основи, і похилою, якщо не перпендикулярні. Бічні грані прямої призми – прямокутники, похилої – паралелограми.

Правильною є призма, в основі якої лежить правильний багатокутник. Якщо в основі призми лежить прямокутник або паралелограм, вона називається паралелепіпедом.

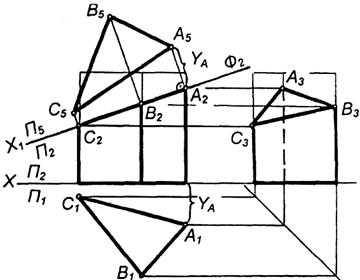Рисунок 91. Переріз призми площиною.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Переріз призми площиною

Рисунок 92. Переріз призми площиною.

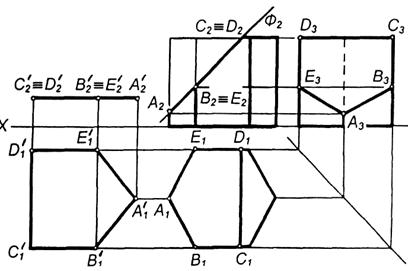Рисунок 93. Переріз призми площиною.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Переріз піраміди площиною

Пірамідою називається багатогранник, одна грань якого (основа) – багатокутник, а бічні грані – трикутники, що мають спільну точку – вершину піраміди.

Ребра піраміди, як і ребра призми, поділяються на бічні й ребра основи.

Піраміда називається правильною, якщо в її основі лежить правильний багатокутник і висота проходить через центр основи. Бічні грані правильної піраміди – рівнобедрені трикутники.

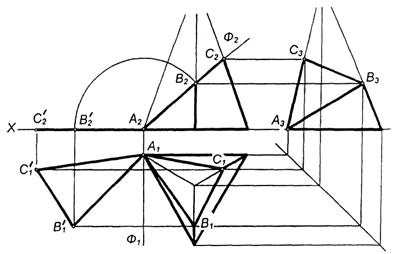Рисунок 94. Переріз піраміди площиною.

Рисунок 95. Переріз піраміди площиною.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Переріз циліндра площиною

Циліндром називається тіло, обмежене циліндричною поверхнею і двома паралельними площинами (основами). Бічну поверхню циліндра отримують обертанням відрізка твірної навколо осі, паралельної цьому відрізку.

Відстань між площинами основ називається висотою.

Циліндри поділяються на прямі, коли твірні перпендикулярні до основ, і похилі.

Оскільки прямий круговий циліндр можна розглядати як пряму призму з численною кількістю ребер – твірних циліндра, то побудова перерізу прямого кругового циліндра аналогічна побудові перерізу призми.

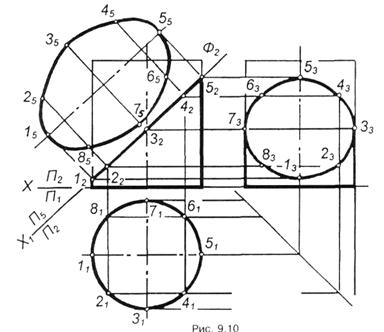Рисунок 96. Переріз циліндра площиною.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Переріз циліндра площиною

Рисунок 97. Переріз циліндра площиною.

Рисунок 98. Переріз циліндра площиною.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Переріз конуса площиною

Конусом називається тіло, обмежене конічною бічною поверхнею і площиною, що перерізає всі його твірні. Бічну поверхню конуса отримують при обертанні відрізка твірної навколо осі, яка перетинає твірну в кожному своєму положенні.

Перпендикуляр, опущений з вершини на площину основи, називається висотою конуса.

Конуси поділяються на прямі й похилі. Прямим коловим називається конус, в основі якого лежить коло, а висота проходить через центр основи.

Рисунок 99. Переріз конуса площиною.

ПЕРЕРІЗ ГЕОМЕТРИЧНИХ ТІЛ ПЛОЩИНАМИ

Переріз конуса площиною

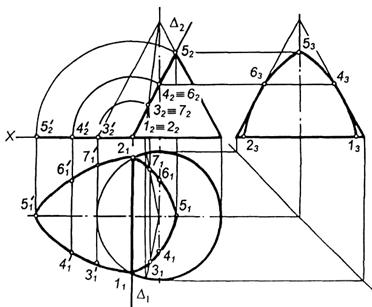Рисунок 100. переріз конуса площиною.

Дата добавления: 2014-10-31