Тема 4.1. Принцип оптимальности и уравнение Беллмана

Решение.

z'_x = 2 х + у - 3, = 2, = 1, z'_y=x + 2 y- 3, 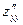= 2.

Решая систему уравнении 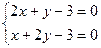получаем точку М₀ (1;1). Так как = АС - В ² = 2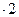2 - 1² = 3 > 0 и A >0, то М₀ (1;1) - точка минимума функции.

Пример. Найти наибольшее и наименьшее значения функции если .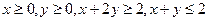

Решение. Областью решения системы неравенств является треугольник АВС (рис.3.8).

Рис. 3.8. Оптимизация функции.

На границе ВС:

Если то Но точка О(0; 0) не входит в треугольник АВС. Вычисляем значение функции на концах отрезка ВС:

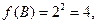
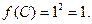
На границе АС:

Если то

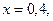
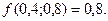
Вычисляем значение функции в точках D(0,4; 0,8) и А(2;0):

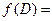
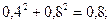
На границе АВ:

f′ =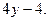

Если f′ = 0, то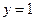, 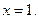Получили точку К(1; 1), причем, Таким образом имеем:

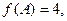
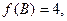
Сравнивая значения функции 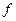в пяти полученных точках, приходим к выводу, что:

РАЗДЕЛ 4 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ.

Динамическое программирование является составной частью математического программирования. Оно используется при решении задач, которые могут быть представлены в виде многошагового процесса. Решение таких задач распадается на отдельные этапы (шаги) и на каждом из них принимается такое решение, которое в конечном итоге приводит к оптимальному результату в целом. Оптимизация целевой функции при решении задачи динамического программирования основана на принципе оптимальности Беллмана: оптимальное поведение обладает тем свойством, что, каковы бы ни были начальное состояние и начальное решение, последующие решения должны соответствовать оптимальному поведению по отношению к состоянию, вытекающему из первого решения. Этот принцип настолько естественен, что некоторые рассматривают его как очевидное утверждение, как аксиому. Из этого принципа вытекает, что для достижения оптимального результата в многошаговом процессе надо на каждом шаге управление (поведение, политику) выбирать с учетом будущего. Так как последний шаг не связан с будущим, то оптимизацию многошагового процесса надо начинать с конца, с планирования последнего шага. Для этого надо использовать все возможные предположения о том, чем может закончиться предпоследний шаг и для каждого из них выбрать управление на последнем шаге. Таким образом, мы приходим к понятию условного оптимального управления (поведения, политики) - оптимального управления, найденного в предположении, что предыдущий шаг окончился так - то. Условное оптимальное управление надо находить, начиная с последнего шага и кончая вторым шагом. На первом шаге с учетом найденных условно оптимальных управлений находится безусловное управление, такое, чтобы получить оптимальное управление для всего процесса.

Обычно принцип оптимального управления многошаговым процессом реализуется с помощью функциональных рекуррентных уравнений Беллмана, вид которых зависит от содержания решаемых задач.

Дата добавления: 2014-10-31