
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Г. Стаханов 3 страница
|
|
|
|
Пример 5.1. Вероятность выхода из строя за время t одного конденсатора равна 0,2. Найти вероятность того, что за время t из 100 конденсаторов выйдут из строя: а) 18 конденсаторов; б) не менее 16 и не более 26 конденсаторов.
Решение. а) по условию p=0.2; n=100; m=18; g=1-0,2=0,8. Поскольку n=100 – достаточно большое число, применим локальную теорему Муавра-Лапласа. Найдём значение
 . Искомая вероятность
. Искомая вероятность 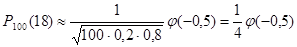 .
.
По таблице значений функции  найдём
найдём 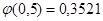 . Следовательно,
. Следовательно, .
.
Б) по условию m1=16, m2=26; n=100; p=0,2; g=0,8. Воспользуемся интегральной теоремой Муавра-Лапласа. Вычислим значения 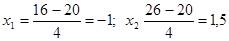 .Учитывая, что функция Лапласа нечётная, получаем
.Учитывая, что функция Лапласа нечётная, получаем  .
.
По таблице значений функции Лапласа найдём Ф(1,5)=0,4332; Ф91)=0,3413. Искомая вероятность  .
.
Пример 5.2. Прядильщица обслуживает 1000 веретён. Вероятность обрыва нити на одном веретене в течение 1 минуты равна 0,004. Найти вероятность того, что в течение 1 минуты произойдёт три обрыва нити.
Решение. По условию n=1000; m=3; p=0.004. Поскольку вероятность появления события в одном испытании мала, а число испытаний достаточно велико, воспользуемся формулой Пуассона (5.1.): 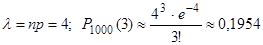 . При вычислении
. При вычислении  использовали таблицу значений функции Пуассона
использовали таблицу значений функции Пуассона  .
.
Пример 5.3. Вероятность того, что деталь стандартная, p=0,9. Сколько нужно отобрать деталей, чтобы с вероятностью  можно было ожидать, что относительная частота появления стандартных деталей (среди отобранных) будет отличаться от вероятности p по абсолютной величине не более чем на 0,037.
можно было ожидать, что относительная частота появления стандартных деталей (среди отобранных) будет отличаться от вероятности p по абсолютной величине не более чем на 0,037.
Решение. По условию p=0,9; g=0,1; 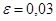 ;
; 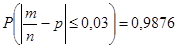 . Найти n. Воспользуемся формулой (5.2):
. Найти n. Воспользуемся формулой (5.2): 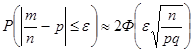 . Введём обозначение
. Введём обозначение  . Тогда 2Ф(t)=0,9876; Ф(t)=0,4938. По таблице значений функции Лапласа найдём Ф(2,5)=0,4838. Следовательно, t=2,5, т.е.
. Тогда 2Ф(t)=0,9876; Ф(t)=0,4938. По таблице значений функции Лапласа найдём Ф(2,5)=0,4838. Следовательно, t=2,5, т.е. 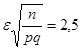 . Для нахождения n получено уравнение
. Для нахождения n получено уравнение  . Отсюда искомое число n=625.
. Отсюда искомое число n=625.
Варианты задачи 6.
|
|
|
Найти вероятность того, что в n независимых испытаниях событие А появится m раз, если вероятность появления события в каждом испытании постоянна и равна р.
| 6.1. | a) | n=100 | m=78 | p=0,8 |
| б) | n=500 | m=2 | p=0,002 | |
| 6.2. | a) | n=400 | m=46 | p=0,1 |
| б) | n=1000 | m=5 | p=0,04 | |
| 6.3. | a) | n=400 | m=310 | p=0,8 |
| б) | n=500 | m=3 | p=0,004 | |
| 6.4. | a) | n=243 | m=75 | p=0,25 |
| б) | n=800 | m=1 | p=0,001 | |
| 6.5. | a) | n=900 | m=825 | p=0,9 |
| б) | n=300 | m=5 | p=0,02 | |
| 6.6. | a) | n=225 | m=188 | p=0,8 |
| б) | n=400 | m=7 | p=0,02 | |
| 6.7. | a) | n=625 | m=380 | p=0,6 |
| б) | n=200 | m=3 | p=0,01 | |
| 6.8. | a) | n=200 | m=50 | p=0,3 |
| б) | n=2000 | m=2 | p=0,02 | |
| 6.9. | a) | n=100 | m=80 | p=0,75 |
| б) | n=1000 | m=4 | p=0,005 | |
| 6.10. | a) | n=300 | m=120 | p=0,4 |
| б) | n=350 | m=8 | p=0,02 | |
| 6.11. | a) | n=400 | m=65 | p=0,2 |
| б) | n=500 | m=2 | p=0,06 | |
| 6.12. | a) | n=100 | m=83 | p=0,8 |
| б) | n=450 | m=8 | p=0,02 | |
| 6.13. | a) | n=200 | m=95 | p=0,5 |
| б) | n=3000 | m=2 | p=0,01 | |
| 6.14. | a) | n=300 | m=75 | p=0,25 |
| б) | n=1500 | m=4 | p=0,002 | |
| 6.15. | a) | n=100 | m=64 | p=0,6 |
| б) | n=600 | m=5 | p=0,01 | |
| 6.16. | a) | n=300 | m=230 | p=0,75 |
| б) | n=700 | m=2 | p=0,001 | |
| 6.17. | a) | n=200 | m=135 | p=0,7 |
| б) | n=250 | m=1 | p=0,004 | |
| 6.18. | a) | n=200 | m=153 | p=0,8 |
| б) | n=4000 | m=6 | p=0,001 | |
| 6.19. | a) | n=144 | m=75 | p=0,5 |
| б) | n=2000 | m=3 | p=0,001 | |
| 6.20. | a) | n=400 | m=190 | p=0,5 |
| б) | n=3000 | m=4 | p=0,001 | |
| 6.21. | a) | n=300 | m=217 | p=0,75 |
| б) | n=100 | m=3 | p=0,02 | |
| 6.22. | a) | n=150 | m=50 | p=0,4 |
| б) | n=500 | m=6 | p=0,01 | |
| 6.23. | a) | n=200 | m=65 | p=0,3 |
| б) | n=1000 | m=2 | p=0,003 | |
| 6.24. | a) | n=144 | m=122 | p=0,8 |
| б) | n=800 | m=5 | p=0,05 | |
| 6.25. | a) | n=100 | m=34 | p=0,4 |
| б) | n=300 | m=4 | p=0,01 | |
| 6.26. | a) | n=300 | m=155 | p=0,5 |
| б) | n=200 | m=6 | p=0,02 | |
| 6.27. | a) | n=250 | m=195 | p=0,8 |
| б) | n=400 | m=2 | p=0,002 | |
| 6.28. | a) | n=196 | m=90 | p=0,5 |
| б) | n=5000 | m=3 | p=0,001 | |
| 6.29. | a) | n=400 | m=290 | p=0,7 |
| б) | n=1000 | m=4 | p=0,006 | |
| 6.30. | a) | n=200 | m=35 | p=0,2 |
| б) | n=250 | m=3 | p=0,02 |
Варианты задачи 7.
Найти вероятность того, что в n независимых испытаниях событие А появится: а) не менее m1 раз и не более m2 раз; б) не более m3 раз; в) не менее m4 раз, если вероятность появления события в каждом испытании постоянна и равна р.
| 7.1. | n=400 | m1=265 | m2=290 | m3=275 | m4=291 | p=0,7 |
| 7.2. | n=100 | m1=75 | m2=85 | m3=74 | m4=86 | p=0,8 |
| 7.3. | n=300 | m1=220 | m2=235 | m3=219 | m4=236 | р=0,75 |
| 7.4. | n=225 | m1=40 | m2=51 | m3=38 | m4=52 | р=0,2 |
| 7.5. | n=245 | m1=140 | m2=155 | m3=139 | m4=150 | р=0,6 |
| 7.6. | n=900 | m1=80 | m2=99 | m3=89 | m4=100 | р=0,1 |
| 7.7. | n=200 | m1=93 | m2=104 | m3=92 | m4=110 | р=0,5 |
| 7.8. | n=400 | m1=350 | m2=369 | m3=355 | m4=370 | р=0,9 |
| 7.9. | n=625 | m1=495 | m2=510 | m3=494 | m4=505 | р=0,8 |
| 7.10. | n=500 | m1=145 | m2=160 | m3=144 | m4=161 | р=0,3 |
| 7.11. | n=100 | m1=46 | m2=53 | m3=45 | m4=58 | р=0,5 |
| 7.12. | n=300 | m1=70 | m2=81 | m3=73 | m4=84 | р=0,25 |
| 7.13. | n=400 | m1=310 | m2=328 | m3=309 | m4=325 | р=0,8 |
| 7.14. | n=250 | m1=94 | m2=108 | m3=95 | m4=110 | р=0,4 |
| 7.15. | n=200 | m1=115 | m2=130 | m3=114 | m4=131 | р=0,6 |
| 7.16. | n=150 | m1=26 | m2=36 | m3=28 | m4=37 | р=0,2 |
| 7.17. | n=100 | m1=85 | m2=94 | m3=84 | m4=95 | р=0,9 |
| 7.18. | n=400 | m1=270 | m2=285 | m3=275 | m4=286 | р=0,7 |
| 7.19. | n=200 | m1=53 | m2=64 | m3=52 | m4=65 | р=0,3 |
| 7.20. | n=144 | m1=110 | m2=120 | m3=109 | m4=118 | р=0,8 |
| 7.21. | n=300 | m1=140 | m2=155 | m3=139 | m4=156 | р=0,5 |
| 7.22. | n=100 | m1=54 | m2=63 | m3=55 | m4=64 | р=0,6 |
| 7.23. | n=225 | m1=172 | m2=185 | m3=171 | m4=183 | р=0,8 |
| 7.24. | n=250 | m1=140 | m2=155 | m3=139 | m4=156 | р=0,6 |
| 7.25. | n=196 | m1=93 | m2=105 | m3=92 | m4=106 | р=0,5 |
| 7.26. | n=150 | m1=56 | m2=66 | m3=55 | m4=67 | р=0,4 |
| 7.27. | n=900 | m1=800 | m2=819 | m3=799 | m4=820 | р=0,9 |
| 7.28. | n=100 | m1=65 | m2=76 | m3=64 | m4=77 | р=0,7 |
| 7.29. | n=400 | m1=196 | m2=207 | m3=195 | m4=208 | р=0,5 |
| 7.30. | n=900 | m1=170 | m2=725 | m3=705 | m4=725 | р=0,8 |
Варианты задачи 8.
|
|
|
8.1.-8.10. Вероятность появления события А в каждом из n независимых испытаний равна р. Найти вероятность того, что относительная частота появления события А будет отличаться от его вероятности по абсолютной величине не более чем на  .
.
| 8.1. | n=625 | р=0,8 |  =0,02 =0,02
|
| 8.2. | n=400 | р=0,5 |  =0,03 =0,03
|
| 8.3. | n=900 | р=0,2 |  =0,02 =0,02
|
| 8.4. | n=1225 | р=0,2 |  =0,01 =0,01
|
| 8.5. | n=100 | р=0,8 |  =0,04 =0,04
|
| 8.6. | n=400 | р=0,75 |  =0,02 =0,02
|
| 8.7. | n=1500 | р=0,6 |  =0,01 =0,01
|
| 8.8. | n=100 | р=0,9 |  =0,045 =0,045
|
| 8.9. | n=1200 | р=0,25 |  =0,015 =0,015
|
| 8.10. | n=600 | р=0,4 |  =0,03 =0,03
|
8.11.-8.20. Вероятность появления события А в каждом из независимых испытаний равна р. Сколько нужно провести испытаний, чтобы можно было ожидать с вероятностью  , что относительная частота появления события А будет отличаться от его вероятности по абсолютной величине не более чем на
, что относительная частота появления события А будет отличаться от его вероятности по абсолютной величине не более чем на  ?
?
| 8.11. | р=0,5 |  =0,92 =0,92
| 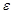 =0,01 =0,01
|
| 8.12. | р=0,6 |  =0,993 =0,993
| 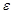 =0,03 =0,03
|
| 8.13. | р=0,9 |  =0,98 =0,98
| 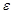 =0,04 =0,04
|
| 8.14. | р=0,8 |  =0,99 =0,99
| 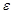 =0,05 =0,05
|
| 8.15. | р=0,5 |  =0,97 =0,97
| 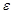 =0,02 =0,02
|
| 8.16. | р=0,75 |  =0,98 =0,98
| 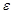 =0,01 =0,01
|
| 8.17. | р=0,9 |  =0,95 =0,95
| 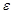 =0,02 =0,02
|
| 8.18. | р=0,25 |  =0,95 =0,95
| 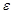 =0,04 =0,04
|
| 8.19. | р=0,7 |  =0,99 =0,99
| 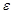 =0,05 =0,05
|
| 8.20. | р=0,8 |  =0,9 =0,9
| 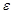 =0,03 =0,03
|
8.21.-8.30. Вероятность появления события А в каждом из n независимых испытаний равна р. Найти такое положительное число  , чтобы с вероятностью
, чтобы с вероятностью  можно было ожидать, что относительная частота появления события А будет отличаться от его вероятности по абсолютной величине не более чем на
можно было ожидать, что относительная частота появления события А будет отличаться от его вероятности по абсолютной величине не более чем на  .
.
| 8.21. | n=600 | р=0,6 |  =0,993 =0,993
|
| 8.22. | n=620 | р=0,5 |  =0,9973 =0,9973
|
| 8.23. | n=400 | р=0,8 |  =0,95 =0,95
|
| 8.24. | n=200 | р=0,9 |  =0,95 =0,95
|
| 8.25. | n=675 | р=0,75 |  =0,9973 =0,9973
|
| 8.26. | n=1200 | р=0,25 |  =0,99 =0,99
|
| 8.27. | n=900 | р=0,2 |  =0,9676 =0,9676
|
| 8.28. | n=100 | р=0,1 |  =0,9 =0,9
|
| 8.29. | n=625 | р=0,8 |  =0,99 =0,99
|
| 8.30. | n=1600 | р=0,5 |  =0,92 =0,92
|
6. ПРОСТЕЙШИЙ ПОТОК СОБЫТИЙ.
Потоком событий называется последовательность событий, которые наступают в случайные моменты времени.
Простейшим (пуассоновским) называется поток событий, который обладает свойствами стационарности, отсутствия последствия и ординарности.
Свойство стационарности состоит в том, что вероятность появления m событий на любом промежутке времени зависит только от числа m и от времени t, и не зависит от начала его отсчёта.
|
|
|
Свойство отсутствия последствия состоит в том, что вероятность появления m событий на любом промежутке времени не зависит от того, сколько событий появилось в моменты времени, предшествующие началу рассматриваемого промежутка.
Свойство ординарности состоит в том, что появление двух и более событий за малый промежуток времени практически невозможно, т.е. за малый промежуток времени может появиться не более одного события потока.
Интенсивность  потока называется среднее число событий, которые появляются за единицу времени.
потока называется среднее число событий, которые появляются за единицу времени.
Если известна постоянная интенсивность потока, то вероятность появления m событий простейшего потока за время t определяется формулой Пуассона:  . (6.1.)
. (6.1.)
Пример 6.1. Среднее число вызовов, поступающих на АТС в 1 минуту, равно двум. Найти вероятность того, что за три минуты поступит: а) четыре вызова; б) менее четырёх вызовов; в) не менее четырёх вызовов. Предполагается, что поток вызовов простейший.
Решение. По условию  =2; t=3; m=4. Воспользуемся формулой Пуассона (6.1.):
=2; t=3; m=4. Воспользуемся формулой Пуассона (6.1.):
а) вероятность того, что за 3 минуты поступит четыре вызова: 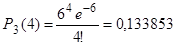 .
.
При вычислении  использовали таблицу значений функции Пуассона.
использовали таблицу значений функции Пуассона.
б) событие «поступило менее четырёх вызовов» произойдёт, если наступит одно из следующих несовместных событий: 1) не поступило ни одного вызова; 2) поступил один вызов; 3) поступило два вызова; 4) поступило три вызова. Применим теорему сложения вероятностей для несовместных событий:

в) событие «поступило менее четырёх вызовов» и «поступило не менее четырёх вызовов» противоположны, поэтому вероятность того, что за три минуты поступит не менее четырёх вызовов,  .
.
Варианты задачи 9.
9.1.-9.6. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, равно  . Найти вероятность того, что за время t часов поступит: а) m заявок; б) менее m заявок; в) не менее m заявок. Предполагается, что поток заявок простейший.
. Найти вероятность того, что за время t часов поступит: а) m заявок; б) менее m заявок; в) не менее m заявок. Предполагается, что поток заявок простейший.
| 9.1. |  =2 =2
| t=2 | m=3 | 9.2. |  =4 =4
| t=2 | m=6 |
| 9.3. |  =3 =3
| t=3 | m=5 | 9.4. |  =6 =6
| t=1 | m=7 |
| 9.5. |  =5 =5
| t=2 | m=6 | 9.6. |  =7 =7
| t=1 | m=5 |
9.7.-9.12. Среднее число заказов такси, поступающих на диспетчерский пункт за 1 минуту равно  . Найти вероятность того, что за t минут поступит: а) m заказов; б) менее m заказов; в) не менее m заказов. Предполагается, что поток заказов простейший.
. Найти вероятность того, что за t минут поступит: а) m заказов; б) менее m заказов; в) не менее m заказов. Предполагается, что поток заказов простейший.
|
|
|
| 9.7. |  =1 =1
| t=5 | m=4 | 9.8. |  =2 =2
| t=3 | m=6 |
| 9.9. |  =4 =4
| t=1 | m=3 | 9.10. |  =3 =3
| t=2 | m=5 |
| 9.11. |  =2 =2
| t=4 | m=4 | 9.12. |  =1 =1
| t=3 | m=4 |
9.13-9.18. Среднее число вызовов, поступающих на АТС за 1 минуту, равно  . Найти вероятность того, что за t минут поступит: а) m вызовов; б) менее m вызовов; в) не менее m вызовов. Предполагается, что поток вызовов простейший.
. Найти вероятность того, что за t минут поступит: а) m вызовов; б) менее m вызовов; в) не менее m вызовов. Предполагается, что поток вызовов простейший.
| 9.13. |  =2 =2
| t=3 | m=5 | 9.14. |  =4 =4
| t=2 | m=7 |
| 9.15. |  =1 =1
| t=7 | m=4 | 9.16. |  =5 =5
| t=1 | m=6 |
| 9.17. |  =3 =3
| t=1 | m=4 | 9.18. |  =1 =1
| t=4 | m=5 |
9.19-9.24. Среднее число кораблей, заходящих в порт за 1 час, равно  . Найти вероятность того, что за t часов в порт зайдут: а) m кораблей; б) менее m кораблей; в) не менее m кораблей. Предполагается, что поток кораблей простейший.
. Найти вероятность того, что за t часов в порт зайдут: а) m кораблей; б) менее m кораблей; в) не менее m кораблей. Предполагается, что поток кораблей простейший.
| 9.19. |  =4 =4
| t=2 | m=5 | 9.20. |  =3 =3
| t=3 | m=6 |
| 9.21. |  =5 =5
| t=2 | m=4 | 9.22. |  =7 =7
| t=1 | m=6 |
| 9.23. |  =6 =6
| t=1 | m=5 | 9.24. |  =2 =2
| t=4 | m=7 |
9.25.-9.30. Среднее число вызовов, поступающих на пункт неотложной медицинской помощи за 1 минуту, равно  . Найти вероятность того, что за t минут поступит: а) m вызовов; б) менее m вызовов; в) не менее m вызовов. Предполагается, что поток вызовов простейший.
. Найти вероятность того, что за t минут поступит: а) m вызовов; б) менее m вызовов; в) не менее m вызовов. Предполагается, что поток вызовов простейший.
| 9.25. |  =1 =1
| t=6 | m=5 | 9.26. |  =2 =2
| t=2 | m=6 |
| 9.27. |  =2 =2
| t=4 | m=6 | 9.28. |  =2 =2
| t=5 | m=5 |
| 9.29. |  =1 =1
| t=2 | m=3 | 9.30. |  =3 =3
| t=2 | m=4 |
7. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 831; Нарушение авторских прав?; Мы поможем в написании вашей работы!