
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интервалы выпуклости и вогнутости. Точки перегиба 1 страница
|
|
|
|
Наибольшее и наименьшее значения функции на отрезке
Чтобы найти наибольшее и наименьшее значения функции 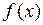 на отрезке
на отрезке 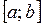 , на котором она непрерывна, надо: найти критические точки, принадлежашие интервалу
, на котором она непрерывна, надо: найти критические точки, принадлежашие интервалу 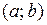 , и вычислить значения функции в этих точках; вычислить значения функции в граничных точках отрезка, т.е.
, и вычислить значения функции в этих точках; вычислить значения функции в граничных точках отрезка, т.е.  и
и 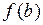 ; из всех полученных значений выбрать наименьшее и наибольшее.
; из всех полученных значений выбрать наименьшее и наибольшее.
Пример 3.19. Найти наибольшее и наименьшее значения функции 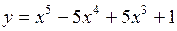 на отрезке
на отрезке  .
.
Решение. Вычислим производную функции и найдем критические точки.
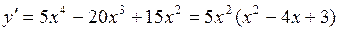 .
.
Производная обращается в ноль в точках 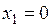 ,
, 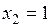 и
и 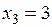 , но
, но 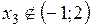 . Следовательно, вычисляем значение функции в критических точках
. Следовательно, вычисляем значение функции в критических точках 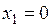 ,
, 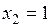 , а также на концах отрезка. Получим:
, а также на концах отрезка. Получим:
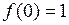 ,
,  ,
, 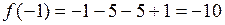 ,
,  . Таким образом, в точке
. Таким образом, в точке  функция принимает наибольшее значение
функция принимает наибольшее значение 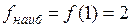 , а в точке
, а в точке 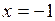 она принимает наименьшее значение
она принимает наименьшее значение 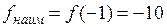 .
.
График функции 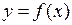 имеет на интервале
имеет на интервале 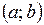 выпуклость, направленную вверх (выпуклый), если все точки графика функции лежат не выше любой своей касательной на этом интервале; график функции
выпуклость, направленную вверх (выпуклый), если все точки графика функции лежат не выше любой своей касательной на этом интервале; график функции 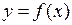 имеет на интервале
имеет на интервале 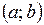 выпуклость, направленную вниз (вогнутый), если все точки графика функции лежат не ниже любой своей касательной на этом интервале.
выпуклость, направленную вниз (вогнутый), если все точки графика функции лежат не ниже любой своей касательной на этом интервале.
Условие выпуклости (вогнутости): если функция 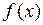 на интервале
на интервале 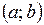 дважды дифференцируема и
дважды дифференцируема и  (
( ) всюду на этом интервале, то график функции выпуклый (вогнутый) на
) всюду на этом интервале, то график функции выпуклый (вогнутый) на 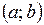 .
.
Точка, отделяющая промежутки выпуклости и вогнутости кривой друг от друга, называется точкой перегиба.
Достаточное условие существования точки перегиба: если при 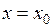 вторая производная функции
вторая производная функции 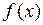 не существует или равна нулю (
не существует или равна нулю ( ) и при переходе через точку
) и при переходе через точку 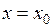 вторая производная
вторая производная  меняет знак, то точка с абсциссой
меняет знак, то точка с абсциссой 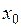 есть точка перегиба графика функции
есть точка перегиба графика функции 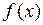 .
.
Пример 3.20. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции  .
.
|
|
|
Решение. Найдем вторую производную заданной функции:
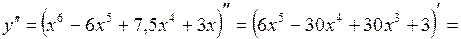
 .
.
Вторая производная обращается в ноль в точках 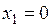 ,
, 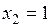 и
и 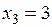 . Все эти точки принадлежат области определения функции. Исследуем знак второй производной:
. Все эти точки принадлежат области определения функции. Исследуем знак второй производной:

Отсюда заключаем, что график функции является выпуклым на интервале 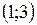 , вогнутым на интервалах
, вогнутым на интервалах 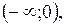
 и
и  . Точки
. Точки 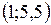 и
и  являются точками перегиба. Точка
являются точками перегиба. Точка 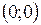 не является точкой перегиба.
не является точкой перегиба.
ВАРИАНТЫ ПРАКТИЧЕСКИХ ТЕСТОВЫХ ЗАДАНИЙ
Вариант 1
1. Найти значение многочлена 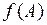 , если
, если 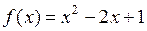 ,
, 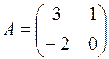 .
.
2. Решить систему линейных уравнений методом Гаусса:
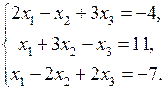
3. Выяснить, лежат ли точки  ,
, 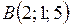 ,
, 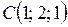 ,
, 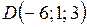 в одной плоскости.
в одной плоскости.
4. Найти расстояние от точки 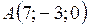 до плоскости
до плоскости  .
.
5. Вычислить пределы:
а)  ; ;
| б) 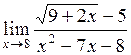 ; ;
|
в) 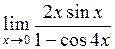 ; ;
| г) 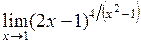 . .
|
6. Вычислить производную 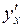 :
:
а)  ; ;
| б) 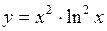 ; ;
|
в) 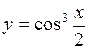 ; ;
| г) 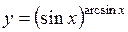 . .
|
7. Вычислить предел, применяя правило Лопиталя:
а)  ; ;
| б) 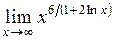 . .
|
8. Найти точки экстремума функции 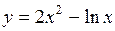 .
.
Ответы: 1. 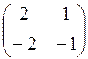 . 2. (1; 3; –1). 3. нет. 4.
. 2. (1; 3; –1). 3. нет. 4.  . 5. а) –1; б)
. 5. а) –1; б)  ; в)
; в)  ; г)
; г)  . 7. а)
. 7. а)  ; б)
; б)  . 8.
. 8.  точка минимума,
точка минимума,  .
.
Вариант 2
1. Вычислить  , если
, если 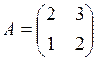 ,
, 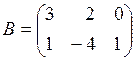 ,
,  .
.
2. Решить систему линейных уравнений по формулам Крамера:
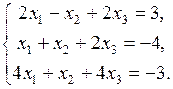
3. Проверить, будут ли векторы  ,
,  ортогональны.
ортогональны.
4. Составить уравнение плоскости, проходящей через точку 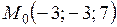 и параллельной двум векторам:
и параллельной двум векторам:  и
и  .
.
5. Вычислить пределы:
а)  ; ;
| б)  ; ;
|
в) 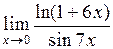 ; ;
| г) 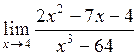 . .
|
6. Вычислить производную 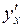 :
:
а) 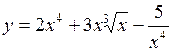 ; ;
| б) 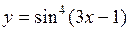 ; ;
|
в) 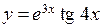 ; ;
| г) 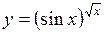 . .
|
7. Вычислить предел, применяя правило Лопиталя:
а)  ; ;
| б)  . .
|
8. Найти точки экстремума функции 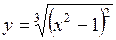 .
.
Ответы: 1. 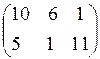 . 2. (1; –3; –1). 3. нет. 4.
. 2. (1; –3; –1). 3. нет. 4.  . 5. а) 3/7; б) 0; в) 6/7; г) 3/16. 7. а) 0; б) 1. 8.
. 5. а) 3/7; б) 0; в) 6/7; г) 3/16. 7. а) 0; б) 1. 8. 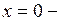 точка максимума,
точка максимума,  и
и  точки минимума,
точки минимума,  .
.
Вариант 3
1. Найти значение многочлена 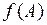 , если
, если 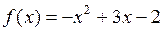 ,
, 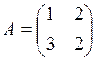 .
.
2. Решить систему линейных уравнений методом обратной матрицы:
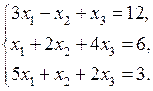
3. Даны два вектора 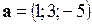 ,
, 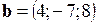 . Найти координаты векторного произведения
. Найти координаты векторного произведения  .
.
4. Составить уравнение плоскости, проходящей через точку  перпендикулярно к вектору
перпендикулярно к вектору  .
.
5. Вычислить пределы:
а)  ; ;
| б)  ; ;
|
в) 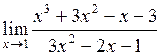 ; ;
| г)  . .
|
6. Вычислить производную 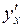 :
:
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 
|
7. Вычислить предел, применяя правило Лопиталя:
|
|
|
а)  ; ;
| б) 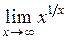 . .
|
8. Найти промежутки монотонности функции  .
.
Ответы: 1.  . 2. (0; –7; 5). 3. (–11; –28; –19). 4.
. 2. (0; –7; 5). 3. (–11; –28; –19). 4. 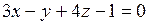 . 5. а) 3; б)
. 5. а) 3; б) 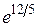 ; в) 2; г) 3/2. 7. а) 0; б) 1. 8. возрастает на
; в) 2; г) 3/2. 7. а) 0; б) 1. 8. возрастает на 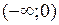 и
и 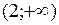 , убывает на
, убывает на 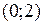 .
.
Вариант 4
1. Найти обратную матрицу 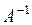 , если
, если 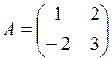 .
.
2. Решить систему линейных уравнений методом Гаусса:
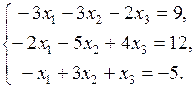
3. Найти угол между векторами 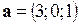 и
и  .
.
4. Составить уравнение плоскости, проходящей через точки  ,
,  ,
, 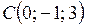 .
.
5. Вычислить пределы:
а)  ; ;
| б) 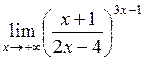 ; ;
|
в) 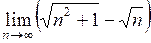 ; ;
| г) 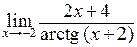 . .
|
6. Вычислить производную 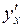 :
:
а) 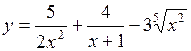 ; ;
| б) 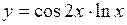 ; ;
|
в)  ; ;
| г) 
|
7. Вычислить предел, применяя правило Лопиталя:
а) 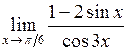 ; ;
| б)  . .
|
8. Найти наибольшее и наименьшее значения функции 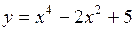 на отрезке
на отрезке  .
.
Ответы: 1. 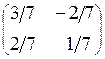 . 2. (–1; –2; 0). 3.
. 2. (–1; –2; 0). 3. 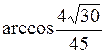 . 4.
. 4. 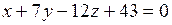 . 5. а) 0; б) 0; в)
. 5. а) 0; б) 0; в)  ; г) 2. 7. а)
; г) 2. 7. а)  ; б) 1. 8.
; б) 1. 8. 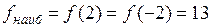 ,
, 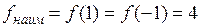 .
.
Вариант 5
1. Найти значение многочлена 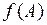 , если
, если  ,
,  .
.
2. Решить систему линейных уравнений по формулам Крамера:

3. Вершины треугольника находятся в точках  ,
,  ,
, 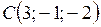 . Вычислить его площадь.
. Вычислить его площадь.
4. Составить уравнение прямой, параллельной вектору  и проходящей через точку
и проходящей через точку 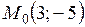 .
.
5. Вычислить пределы:
а) 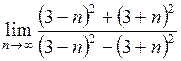 ; ;
| б)  ; ;
|
в) 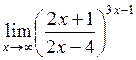 ; ;
| г)  . .
|
6. Вычислить производную 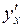 :
:
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 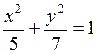 . .
|
7. Вычислить предел, применяя правило Лопиталя:
а) 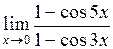 ; ;
| б) 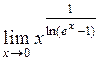 . .
|
8. Найти точки экстремума функции  .
.
Ответы: 1. 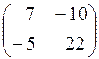 . 2. (1; 6; 5). 3.
. 2. (1; 6; 5). 3. 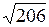 . 4.
. 4.  . 5. а)
. 5. а) 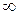 ; б) –1/48; в)
; б) –1/48; в) 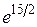 ; г) –2. 7. а)
; г) –2. 7. а) 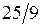 ; б)
; б) 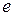 . 8.
. 8. 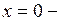 точка минимума,
точка минимума, 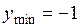 .
.
Вариант 6
1. Даны матрицы 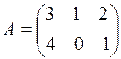 ,
, 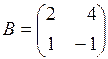 ,
, 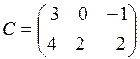 . Найти значение
. Найти значение 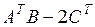 .
.
2. Решить систему линейных уравнений методом обратной матрицы:
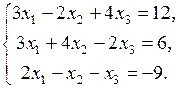
3. Вычислить, при каких значениях 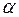 и
и 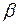 векторы
векторы 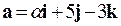 и
и 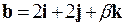 коллинеарны.
коллинеарны.
4. Найти угол между прямыми 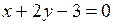 и
и 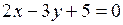 .
.
5. Вычислить пределы:
а)  ; ;
| б)  ; ;
|
в) 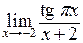 ; ;
| г)  . .
|
6. Вычислить производную 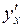 :
:
а) 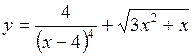 ; ;
| б)  ; ;
|
в) 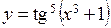 ; ;
| г) 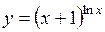 . .
|
7. Вычислить предел, применяя правило Лопиталя:
а) 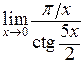 ; ;
| б)  . .
|
8. Найти точки перегиба функции 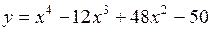 .
.
Ответы: 1. 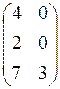 . 2. (0; 4; 5). 3.
. 2. (0; 4; 5). 3.  ,
, 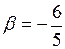 . 4.
. 4.  . 5. а) 5/2; б)
. 5. а) 5/2; б) 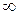 ; в)
; в)  ; г) 0. 7. а)
; г) 0. 7. а)  ; б)
; б) 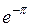 . 8.
. 8. 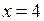 и
и 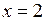 – точки перегиба.
– точки перегиба.
Вариант 7
1. Найти значение многочлена 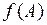 , если
, если  ,
,  .
.
2. Решить систему линейных уравнений методом Гаусса:

3. Найти объем параллелепипеда, построенного на векторах  ,
, 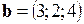 ,
, 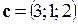 .
.
4. Составить каноническое уравнения прямой, проходящей через точки  и
и  .
.
5. Вычислить пределы:
а)  ; ;
| б) 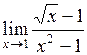 ; ;
|
в)  ; ;
| г) 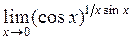 . .
|
6. Вычислить производную 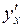 :
:
а)  ; ;
| б) 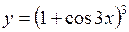 ; ;
|
в) 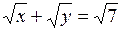 ; ;
| г) 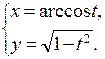
|
7. Вычислить предел, применяя правило Лопиталя:
а)  ; ;
| б)  . .
|
8. Найти промежутки монотонности функции 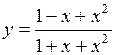 .
.
Ответы: 1. 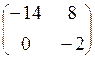 . 2. (3; –1; –4). 3. 15. 4.
. 2. (3; –1; –4). 3. 15. 4.  . 5. а)
. 5. а) 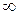 ; б) 1/4; в) 1/3; г)
; б) 1/4; в) 1/3; г) 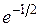 . 7. а) 4/9; б) 1. 8. возрастает на
. 7. а) 4/9; б) 1. 8. возрастает на 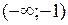 и
и 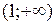 , убывает на
, убывает на 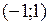 .
.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 865; Нарушение авторских прав?; Мы поможем в написании вашей работы!