Математическая основа карт

Земной эллипсоид.

Известно, что Земля шарообразна, т.е. не обладает формой идеального шара. Фигура ее направлена, и, как всякое вращающееся тело, она немного сплюснута у полюсов. Кроме того, из-за неравномерного распределения масс земного вещества и глобальных тектоноческих деформаций выпуклости и вогнутости. Сложную фигуру нашей планеты, ограниченную уровенной поверхностью океана называют геоиды. Точно определить его форму практически невозможно, но современные высокоточные измерения со спутников позволяют иметь о нем достаточно хорошее представление и даже описать уравнением.

Наилучшее геометрическое приближение к реальной фигуре Земли дает эллипсоид-вращения – геометрическое тело, которое образуется при вращении эллипса вокруг его малой оси.

В России принят референц-эллипсоид Ф.Н. Красовского вычисленный в 1940 г. Его параметры таковы:

- большая полуось (а) – 6378245 м

- малая полуось (b) – 6356863 м

- сжатие α=(a-b)/a – 1:298,3

В США и Канаде до недавнего времени использовали эллипсоид Кларка, рассчитанный еще в 1866 г. Его большая полуось на 39 м короче, чем в российском эллипсоиде, а сжатие определено в 1:295,0.

В 1984 г. на основе спутниковых измерений вычислен международный эллипсоид WGS-84 (World Geodetic System). Всего в мире насчитывается около полутора десятка разных эллипсоидов.

Для принятия единого международного эллипсоида требуется перевычислить координаты, и пересоставить все карты, а это долгое, сложное, а главное дорогостоящее дело. Несовпадения бывают заметны, главным образом, на крупномасштабных картах при определении по ним точных координат объектов. Но на широко используемых географами средне- и мелкомасштабных картах такие различия не очень чувствительны. Более того, иногда вместо эллипсоида берут шар и тогда в качестве среднего радиуса Земли принимают R=6367,6 км. Погрешности при замене эллипсоида шаром оказываются столь малы, что никак не проявляются на большинстве географических карт.

Для того чтобы добиться наименьших искажений, применяют также способ двойного проектирования; сперва эллипсоид проектируют на шар, а затем шар на плоскость.

Масштаб карты – степень уменьшения объектов на карте относительно их размеров на земной поверхности (точнее, на поверхности эллипсоида).

Строго говоря, масштаб постоянен только на планах, охватывающих небольшие участки территории. На географических картах он меняется от места к месту и даже в одной точке – по разным направлениям, что связано с переходом от сферической поверхности планеты к плоскому изображению. Поэтому различают главный и частный масштабы карт.

Главный масштаб показывает, во сколько раз линейные размеры на карте уменьшены по отношению к эллипсоиду или шару. Этот масштаб подписывают не карте, но необходимо иметь ввиду, что он справедлив лишь для отдельных линий и точек, где искажения отсутствуют.

Частный масштаб отражает соотношение размеров объектов на карте и эллипсоиде (шаре) в данной точке. Он может быть больше или меньше главного. Частный масштаб длин μ показывает отношение длины бесконечно малого отрезка на карте ds’ к длине бесконечно малого отрезка ds’ на поверхности эллипсоида или шара, а частный масштаб площадей р передает аналогичные соотношения бесконечно малых площадей на карте dp’ и эллипсоиде или шаре dр’.

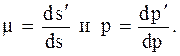
В общем случае, чем мельче масштаб картографического изображения и чем обширнее территория, тем сильнее сказываются различия между главным и частным масштабами.

В России для топографических и обзорно-топографических карт установлена система масштабов

1:5000

1:10000

1:25000

1:50000

1:100000

1:200000

1:300000

1:500000

1:1000000

Масштаб указывается на картах в разных вариантах.

Численный масштаб – представляет собой дробь с единицей в числителе, он показывает, во сколько раз длины на карте меньше соответствующих длин на местности (например. 1:1000000).

Линейный (графический) масштаб дается на полях карты в виде линейки, разделенной на равные части (обычно см) с подписями означающими соответствующие расстояния на местности. Он удобен для измерений на карте.

Именованный масштаб указывается в виде подписи, какое расстояние на местности соответствует одному сантиметру на карте (например, в 1 см – 1 км).

Картографическая проекция – это математически определенное отображение поверхности эллипсоида или шара (глобуса) на плоскость карты.

Проекция устанавливает однозначное соответствие между геодезическими координатами точек (широтой В и долготой L и их прямоугольными координатами Х и Y) на карте. Уравнения проекций в общей форме выглядят предельно просто.

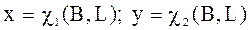
Конкретные реализации функции χ₁ и χ₂ часто выражены довольно сложными математическими зависимостями, их число бесконечно, а следовательно, разнообразие картографических проекций практически неограниченно.

Теория картографических проекций составляет главное содержание математической картографии. В этом разделе разрабатывают методы изыскания новых проекций для разных проекций, оценки распределения и величин искажений. Особый круг задач связан с учетом этих искажений при измерениях по картам, переходом из одной проекции в проекции с заданными свойствами.

Исходная аксиома при искажении любых картографических проекций состоит в том, что сферическую поверхность земного шара (эллипсоида, глобуса) нельзя развернуть на плоскости карты без искажений.

Неизбежно возникают деформации сжатия и растяжения. различные по величине и направлению. именно поэтому на карте возникает непостоянно масштабов длин и площадей.

В картографических проекциях могут присутствовать следующие виды искажений:

- искажение длин; вследствие этого масштаб карты непостоянен в разных точках и по разным направлениям, а длины линий и расстояния искажены;

- искажение площадей; масштаб площадей в разных точках карты различен, что является прямым следствием искажений длин и нарушает размеры объектов;

- искажение углов; углы между направлениями на карте искажены относительно тех же углов на местности;

- искажение форм; фигуры на карте деформированы и не подобны фигурам на местности, что прямо связано с искажением углов.

Любая бесконечно малая окружность на карте (эллипсоиде) предстает на карте бесконечно малым эллипсом, его называют эллипсом искажений. Для наглядности вместо бесконечно малого эллипса обычно рассматривают эллипс конечных размеров.

а – направление наибольшего растяжения масштаба b – направление наибольшего сжатия масштаба m – масштаб по меридиану n – масштаб по параллели

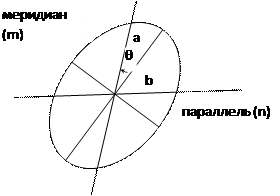
Его размеры и форма отражают искажения длин, площадей и углов, а ориентировка большой оси относительно меридиана и параллели – направление наибольшего расстояния. Большая ось эллипса искажений характеризует наибольшее растяжение в данной точке, а малая ось – наибольшее сжатие, отрезки вдоль меридиана и параллели соответственно характеризуют частные масштабы по меридиану m и параллелям n.

Определив значения m и n, а также измерив угол θ, под которым пересекаются на карте меридиан и параллель, можно затем рассчитать значения наибольшего а и наименьшего b частных масштабов длин, частный масштаб площадей р в данной точке, а также значение искажения углов ω по формулам:

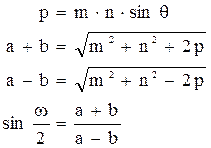
Если главные оси эллипса ориентированы по меридиану и параллели, то

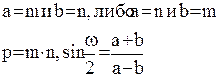
Значения m, n, a, b и р измеряют в процентах или в долях от главного масштаба. например, если а =1,12, то это означает, что частный масштаб по направлению большой оси эллипса искажений составляет 1,12 (или 112%) от главного масштаба. Иногда в качестве показателей искажений используют их отклонения от единицы: m -1, n -1, a -1, b -1 и р -1 – эти показатели называют относительными множителями. Если, например, а -1=0,12, то это значит, что частный масштаб вдоль большой оси эллипса искажений преувеличен относительно главного масштаба на 0,12 (или на 12%).

Частный масштаб может оказаться и меньше главного, например b =0,85 (85%), т.е. масштаб преуменьшен на 0,15 (на 15%).

В ряде проекций существуют линии и точки, где искажения отсутствуют и сохраняется главный масштаб карты – это линии и точки нулевых искажений. Для наиболее употребительных проекций существуют специальные вспомогательные карты, на которых показаны эти линии и точки, и кроме того приведены изоколы – линии равных искажений длин, площадей, углов и форм. При определении размеров искажений в заданной точке можно воспользоваться картами изокол, либо провести несложные измерения, а затем вычисления по приведенным выше формулам.

Классификация проекций по характеру искажений

Равновеликие проекции сохраняют площади без искажений. Такие проекции удобные для измерения площадей объектов, однако, в них значи-

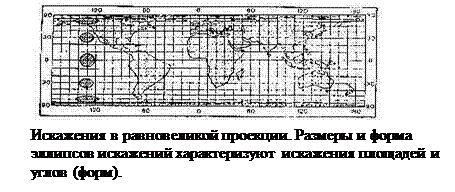
тельно нарушены углы и формы, что особенно заметно для больших территорий. Например, на карте мира приполярные области выглядят сильно сплющенными.

Равноугольные проекции оставляют без искажений углы и формы контуров, показанных на карте (ранее такие проекции называли конфорными). Элементарная окружность в таких проекциях всегда остается окружностью, но размеры ее сильно меняются.

Такие проекции особенно удобные для определения направления и прокладки маршрутов по заданному азимуту, поэтому их всегда используют на навигационных картах. Зато карты, составленные в равноугольных проекциях, имеют значительные искажения площадей.

Равнопромежуточные проекции – произвольные проекции, в которых масштаб длин по одному из главных направлений постоянен и обычно равен главному масштабу карты. Соответственно различают проекции равнопромежуточные по меридианам – в них без искажений остается масштаб вдоль меридианов, и равнопромежуточными по параллелям – в них сохраняется постоянным масштаб вдоль параллелей. В таких проекциях присутствуют искажения площадей и углов, но они как бы уравновешиваются.

Произвольные проекции – это все остальные виды проекций, в которых в тех или иных произвольных соотношениях искажаются и площади, и углы (формы). При их построении стремятся найти наиболее выгодное для каждого конкретного случая распределение искажений, достигая как бы некоторого компромисса. Скажем, выбирают проекции с минимальными искажениями в центральной части карты «сбрасывая» все сжатия и растяжения к краям.

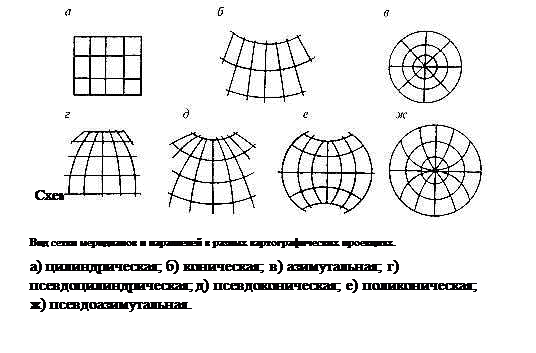
Классификация проекций по виду нормальной картографической сетки

Вспомогательными поверхностями при переходе от эллипсоида или шара к карте могут быть плоскость, цилиндр, конус, серия конусов и некоторые другие геометрические фигуры.

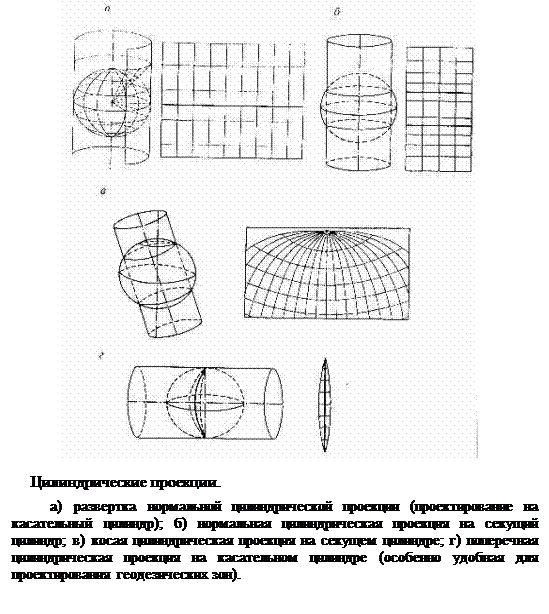Цилиндрические проекции – проектирование шара (эллипсоида) ведется на поверхность касательно или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость

Если ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по экватору (или сечет его по параллелям). то проекция называется нормальной (прямой) цилиндрической. Тогда меридианы нормальной сетки представляют в виде равноотстоящих параллельных прямых, а параллели – в виде прямых, перпендикулярных к ним. В этих проекциях меньше всего искажений в тропических и приэкваторных областях.

Если ось цилиндра расположена в плоскости экватора, то это – поперечная цилиндрическая проекция. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют и, следовательно, в такой проекции наиболее выгодно изображать территории, вытянутые с севера на юг. В тех случаях, когда ось вспомогательного цилиндра расположена под углом к плоскости экватора, проекция называется косой цилиндрической. Она удобна для вытянутных территорий ориентированных на северо-запад или северо-восток.

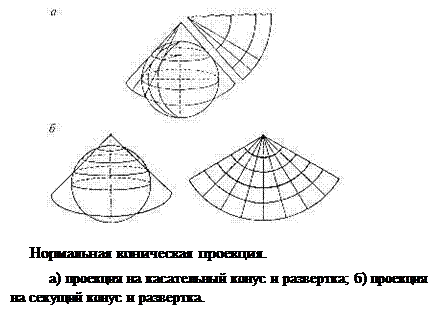Конические проекции – поверхность шара (эллипсоида) преоктируются на поверхность касательного или секущего конуса, после чего она как бы разрезается по образующей и разворачивается в плоскость.

Как и в предыдущем случае различают нормальную (прямую) коническую проекцию, когда ось конуса совпадает с осью вращения Земли, поперечную коническую – ось конуса лежит в плоскости экватора и косую коническую – ось конуса наклонена к плоскости экватора.

В нормальной конической проекции меридианы представляют собой прямые, расходящиеся из точки полюса, а параллели – дуги концентрических окружностей. Воображаемый конус касается земного шара или сечет его в районе средних широт, поэтому в такой проекции удобнее всего картографировать территории России, Канады, США, вытянутые с Запада на Восток в средних широтах.

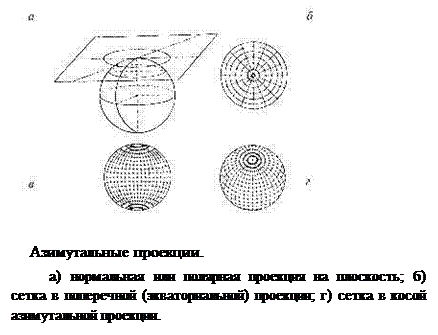
Азимутальные проекции – поверхность земного шара (эллипсоида) перекосится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная) азимутальная проекция.

Параллели в ней являются концентрическими окружностями, а меридианы – радиусами этих окружностей. В этой проекции всегда картографируют полярные области нашей и других планет.

Если плоскость проекции перпендикулярна к плоскости экватора, то получается поперечно (экваториальная) азимутальная проекция. Она всегда используется для карт полушарий.

А если проектирование выполнено на касательную или секущую вспомогательную плоскость, находящуюся под любым углом к плоскости экватора, то получается косая азимутальная проекция.

Условные проекции – проекции, для которых нельзя подобрать простых геометрических аналогов. Их строят, исходя из каких-либо заданных условий, например, желательного вида географической сетки, того или иного распределения искажений на карте заданного вида сетки и др. В частности, к условным принадлежат псевдоцилиндрические, псевдоконические, псевдоазимутальные и другие проекции, полученные путем преобразования одной или нескольких исходных проекций.

Многогранные проекции – проекции, получаемые путем проектирования шара (эллипсоида) на поверхность касательного или секущего многогранника.

Чаще всего каждая грань представляет собой равнобочную трапецию, хотя возможны и другие варианты (например, шестиугольник, квадрат, ромб). Разновидностью многогранных является многополосные проекции, причем полосы могут «нарезаться» и по меридианам, и по параллелям. Такие проекции выгодны тем, что искажения в пределах каждой грани или полосы совсем невелики, поэтому их всегда используют для многолистных карт. Рамка каждого листа, составленного в многогранной проекции, представляет собой трапецию, образованную линиями меридианов и параллелей. За это приходится «расплачиваться» – блок листов карт нельзя совместить по общим рамкам без разрывов.

В первой половине XIX в. земной эллипсоид заменяли многогранником, вписанным в эллипсоид (или описанный около него) и самостоятельно изображали отдельную грань. Позднее для топографических карт многих стран стали использовать равноугольную поперечную цилиндрическую проекцию Гаусса-Крюгера. Для ее применения поверхность эллипсоида разделяется на сфероидические двуугольники (геодезические зоны), каждая из которых изображается на плоскости самостоятельно. Таким образом, «многогранная проекция» заменена «многополосной», она создает разрывы по краям зон, но позволяет соединять в одно целое листы внутри всей зоны и считать в пределах зоны масштаб практически постоянным.

Сегодня топографические карты в России создают в поперечно-цилиндрической проекции Гаусса-Крюгера, а в США и многих других западных странах – в универсальной поперечно-цилиндрической проекции Меркатора (сокращенно ИТМ). Обе проекции близки по своим свойствам, и та и другая по существу являются многополосными.

Дата добавления: 2014-10-31