Скалярное произведение векторов

Пусть и - произвольные векторы, а j - угол между ними:

j

Определение. Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

×= ïïïïcosj (3.1)

Свойства скалярного произведения:

1) ×= ×- переместительный закон;

2) (a)×= ×(a) = a(×), a=const – сочетательный закон относительно умножения на число;

3) ×(+) = ×+ ×- распределительный закон относительно суммы векторов;

4) ×= ²= ïï² (3.2) – формула скалярного квадрата.

×= çç×çç×cos(,) = ïï² cos0° = ïï².

Из (3.2) Þ ïï = - длина вектора равна корню квадратному из его скалярного квадрата.

5) ×= 0, если ^и наоборот, если ×= 0, то при ¹ 0 и ¹ 0 векторы и взаимно перпендикулярны – это условие перпендикулярности двух векторов:

^ Û ×= 0 (3.3)

Если рассматривать векторы 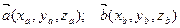в декартовой прямоугольной системе координат, то

×= x_a x_b + y_a y_b + z_a z_b (3.4) - скалярное произведение векторов в координатной форме

Используя полученные равенства (3.1) и (3.4), получаем формулу для вычисления угла между векторами:

(3.5)

Пример. Найти (5+ 3)(2- ), если

Пример. Найти угол между векторами и , если

.

Пример. Найти скалярное произведение (3- 2)×(5- 6), если

Пример. При каком m векторы и 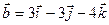перпендикулярны.

Пример. Найти скалярное произведение векторов и 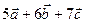, если

§5.Векторное произведение векторов.

Определение. Векторным произведением векторов и называется вектор 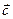, удовлетворяющий следующим условиям:

1) 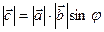, где j - угол между векторами и ,

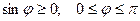
2) вектор 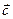ортогонален векторам и

3) , и 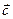образуют правую тройку векторов.

Обозначается: 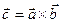или .

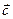
j

Свойства векторного произведения векторов:

1) ;

2) 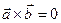, если ïïили = 0 или = 0;

3) (m)´= ´(m) = m(´);

4) ´(+ ) = ´+ ´ ;

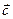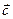5) Если заданы векторы (x_a, y_a, z_a) и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами 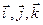, то

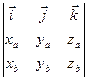´= (4.1)

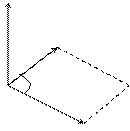
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

Пример. Найти векторное произведение векторов и

.

.

Дата добавления: 2014-10-31