
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные определения и обозначения
Задачи для самостоятельного решения
а) Написать уравнение прямой, проходящей через точку А (2, 0, -3) параллельно:
1) вектору 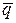 =(2, -3, 5);
=(2, -3, 5);
2) прямой (х - 1)/5 = (у + 2)/2 = (z + 1)/(-1);
3) прямой 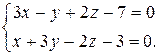
б) Задана плоскость x + y - z + 1 = 0 и прямая (x - 1)/0 = y /2 = (z + 1)/1.
Требуется:
1) вычислить угол между ними;
2) написать уравнение плоскости, проходящей через данную прямую перпендикулярно к данной плоскости.
в) Доказать, что прямые
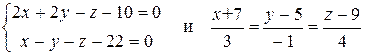
параллельны, и найти расстояние между ними.
г) Найти проекцию точки С (3, -4, -2) на плоскость, проходящую через параллельные прямые

10. ВВЕДЕНИЕ В АНАЛИЗ
Определение конечного предела функции в точке: число А называется пределом функции 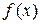 при
при  если для любого
если для любого  найдется
найдется 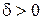 такое, что
такое, что 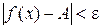 при 0 <
при 0 < 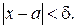
Обозначение: 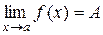 или
или 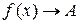 при
при 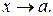
Функция 
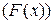 называется бесконечно малой (бесконечно большой) при
называется бесконечно малой (бесконечно большой) при  если
если 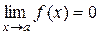
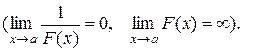
Две бесконечно малые (бесконечно большие) функции 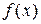 и
и 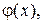 при
при  называются эквивалентными, если
называются эквивалентными, если 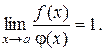
Обозначение: 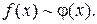
Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной функцией, т.е.
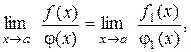 (10.1)
(10.1)
если 
Отметим, что (С - константа)


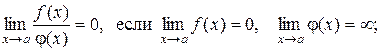
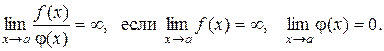
Наиболее простым способом вычисления пределов 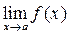 является непосредственная подстановка вместо х числа а. При этом может получится какое-либо число, которое и является пределом. Например
является непосредственная подстановка вместо х числа а. При этом может получится какое-либо число, которое и является пределом. Например
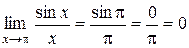 .
.
Второй также несложный случай возникает, если при такой непосредственной подстановке одна из составляющих имеет предел равный ¥ и получаются следующие варианты (и их решение): С /¥ = 0, С /0 = ¥, ¥/0 = ¥, 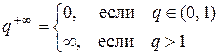 ,
, 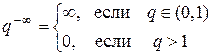 . Например
. Например
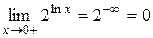 .
.
В остальных случаях возникают так называемые неопределенности. По поведению функций пределы делятся на неопределенности вида: 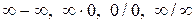 ,
, 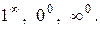 Элементарными приемами раскрытия неопределенностей являются:
Элементарными приемами раскрытия неопределенностей являются:
а) сокращение на множитель, создающий неопределенность;
б) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при  );
);
в) применение эквивалентных бесконечно малых и бесконечно больших;
г) использование двух замечательных пределов:
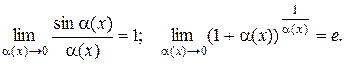 (10.2)
(10.2)
10.2. Неопределенности вида 0/0
а) Рациональные выражения. В случае неопределенности 0/0 для рациональных выражений всегда применяется прием сокращения множителя, обращающегося в ноль. Для этого предварительно выделяется линейный множитель, который обращается в ноль. Для выделения линейного множителя находят корни квадратного трехчлена и разлагают его на множители.
Пример. Найти предел
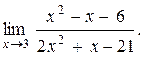
Находим корни числителя х2 - х - 6: х 1 = 3, х 2 = -2.Разлагаем его на множители х2 - х - 6 = (х – 3)(х + 2). То же самое проделываем и для знаменателя: х 1 = 3, х 2 = -7/2, 2х2 + х - 21 = 2(х – 3)(х + 7/2) =
= (х – 3)(2 х + 7). Подставим эти разложения в предел и сокращаем множители, обращающиеся в ноль:
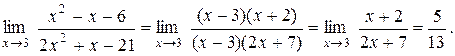
б) Иррациональные выражения. Пределы вычисляются также сокращением множителя, обращающегося в предельной точке в ноль. Правда предварительно для этого иррациональное выражение домножают и делят на сопряженное выражение, т.е., если выражение имеет вид (a ± b), то его домножают и делят на (a  b).
b).
Пример. Найти предел
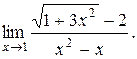
Домножим числитель и знаменатель на выражение  , одновременно разлагая знаменатель на множители:
, одновременно разлагая знаменатель на множители:
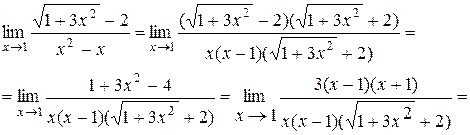
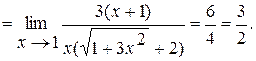
в) Выражения, содержащие тригонометрические и обратные тригонометрические функции. Вычисление пределов в этом случае, как правило, проводится по следующим трем методикам:
1) использование первого замечательного предела
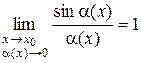
или эквивалентности:
sin a(x) ~ a(x) при a(x) ® 0 (x ® x 0);
2) использование формул тригонометрии;
3) применение замены для сведения к первому замечательному преде-лу.
Примеры.
а) Найти предел
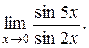
Воспользуемся приведенными эквивалентностями:
sin 5 x ~ 5 x, sin 2 x ~ 2 x при x ® 0.
Тогда
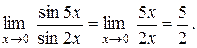
б) Найти предел
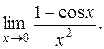
По формулам тригонометрии (1 - cos x = 2 sin2 (x/ 2)) с учетом эквивалентности имеем

в) Найти предел
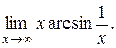
Для сведения к первому замечательному пределу сделаем две замены:
у = 1 /х, z = arcsin y:
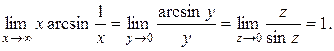
г) Найти предел
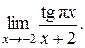
Сделаем замену переменной: у = х + 2. Тогда (с учетом периодичности тангенса и эквивалентности)
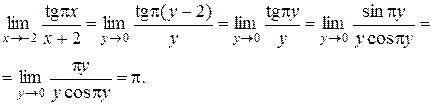
г) Выражения, содержащие логарифмические и показательные функции. Основными приемами вычисления пределов в этом случае являются:
1) использование эквивалентностей
ln(1 + a(x)) ~ a(x), a a (x) - 1 ~ a(x)ln a при a(х) ® 0;
2) замена переменной для сведения к приведенным эквивалентностям.
Примеры.
а) Найти предел
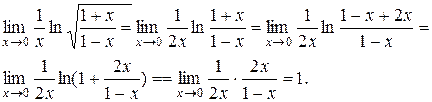
б) Найти предел
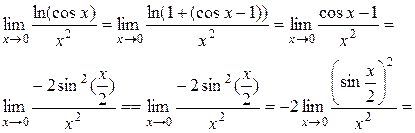
=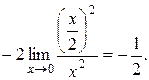
10.3. Неопределенности вида ¥/¥
Основными примерами этой неопределенности являются рациональные функции, когда аргумент стремится к бесконечности. Решаются они вынесением в числителе и знаменателе наивысшей степени х и ее сокращением. При вычислении окончательного результата постоянно используется равенство С /¥ = 0 (C -константа).
Пример. Найти предел

Выносим наивысшую степень х в числителе и знаменателе:
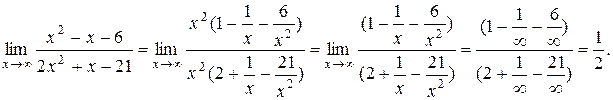
10.4. Неопределенности вида ¥ - ¥, 0×¥, 00, ¥0, 1¥
Первые четыре неопределенности с помощью арифметических преобразований сводятся к рассмотренным ранее случаям. Особый интерес представляет последняя неопределенность. Для вычисления пределов с неопределенностью 1¥ очень удобна следующая формула:
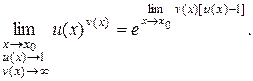
Примеры.
а) Найти предел
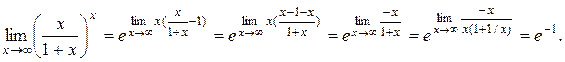
б) Найти предел
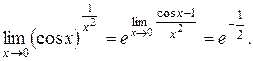
При вычислении подобных примеров наибольшую опасность представляет путаница, возникающая в связи с тем, что к определенным выражениям (типа (2/3)¥ = 0) применяют формулу, как для неопределенности вида 1¥. Например
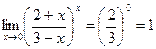 или
или
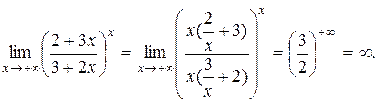
|
|
Дата добавления: 2014-10-31; Просмотров: 405; Нарушение авторских прав?; Мы поможем в написании вашей работы!