Лекция 2. Точные методы исследования устойчивости и автоколебаний. Метод фазовых траекторий

Методы исследования нелинейных систем

Наличие нелинейных зависимостей в САУ приводит к описанию состояния этой системы нелинейными дифференциальными уравнениями. Как известно, большинство групп нелинейных уравнений не решается в общем виде, и можно лишь говорить о частных случаях решений. Поэтому при исследовании нелинейных систем большую роль приобретают различные приближенные методы.

Посредством приближенных методов исследования нелинейных систем нельзя, как правило, получить достаточно полное представление о всех динамических свойствах системы, однако с их помощью можно ответить на ряд отдельных существенных вопросов, таких как вопрос устойчивости, наличия автоколебаний, характера каких-либо частных режимов и т.п.

Но системы релейного типа (характеристики которых состоят только из горизонтальных и вертикальных прямых) удается исследовать полностью, используя аппарат линейных дифференциальных уравнений.

В настоящее время существует большое число различных аналитических и графо-аналитических методов исследования нелинейных систем. Из них наиболее разработаны методы исследования их устойчивости, которые удобно разделить на две большие группы: точные методы и приближенные методы.

Точные методы исследования устойчивости и автоколебаний.

Метод фазовых траекторий

Сущность его заключается в следующем. Допустим, что совокупность уравнений, описывающих систему n -го порядка, может быть представлена в виде n -уравнений первого порядка:

(2.1)

где - независимые переменные, определяющие состояние системы; 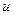и - управляющие и возмущающие воздействия.

Каждому состоянию системы соответствуют определенные значения переменных 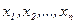. Эти переменные можно представить в виде прямоугольных координат некоторой точки , которую будем называть изображающей точкой. Если с течением времени происходит изменение независимых координат 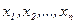, то это означает, что изображающая точка перемещается в данной системе координат, прочерчивая кривую, называемую фазовой траекторией (рисунок 2.5).

Рисунок 2.5 Трехмерное фазовое пространство

Направление движения изображающей точки обозначается на фазовой траектории стрелками. Пространство, в котором движется изображающая точка , называется фазовым пространством (пространством состояния).

В системе, описываемой, дифференциальным уравнением второго порядка будут, только две независимые переменные и . В этом случае фазовое пространство вырождается в фазовую плоскость. Фазовая траектория представляет собой плоскую кривую (рисунок 2.6). По оси абсцисс откладывается исследуемая переменная 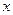, а по оси ординат – ее первая производная .

Рисунок 2.6 Фазовая плоскость

В системе, описываемой, дифференциальным уравнением третьего порядка будут, три независимые переменные . В этом случае фазовое пространство получается трехмерным (рисунок 2.5).

В общем случае дифференциального уравнения n -го порядка получается n-мерное фазовое пространство. Ввиду серьезных трудностей, возникающих при рассмотрении n- мерного пространства, метод фазовых траекторий обычно применяется для систем второго порядка. Фазовые траектории дают, вообще говоря, только качественную оценку процессов регулирования, так как по этому методу время в явном виде не включено.

Рассмотрим изображение типичных процессов на фазовой плоскости. Если уравнения (2.1) составлены в отклонениях, а 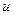и равны нулю, то установившееся состояние характеризуется значениями 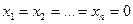. Следовательно, изображением установившегося состояния служит начало координат фазового пространства.

Отсюда вытекает, что фазовые траектории устойчивой линейной системы в ее свободном движении будут асимптотически приближаться к началу координат. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.

Для нелинейных систем вследствие особенностей их процессов фазовые траектории могут принимать самые разнообразные очертания.

Затухающий колебательный процесс.

Начальная точка процесса (рисунок 2.7,а) имеет определенные значения и и 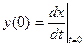на фазовой плоскости (рисунок 2.7,б) изобразится в виде изображающей точки 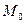. На участке процесса , 1 величина 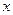увеличивается, а производная 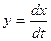уменьшается. На участке 1, 2 процесс идет с уменьшением координаты 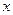при отрицательной производной 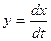. Рассуждая аналогично, далее получим последующие участки фазовой траектории, соответствующие участкам переходного процесса. В результате видим, что сходящемуся колебательному процессу соответствует фазовая траектория, сходящаяся к началу координат. Начало координат в этом случае называется устойчивым фокусом.

Рисунок 2.7 Сходящийся колебательный процесс

Расходящийся колебательный процесс (рисунок 2.8а) изобразится в виде спиральной фазовой траектории, удаляющейся от начала координат (рисунок 2.8б). Начало координат фазовой плоскости в этом случае называется неустойчивым фокусом.

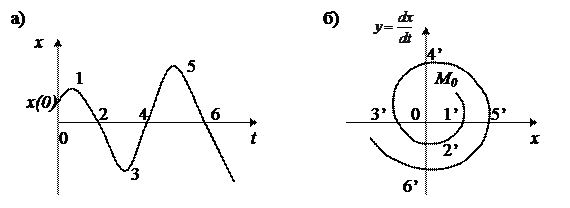
Рисунок 2.8 Расходящийся колебательный процесс

Монотонные сходящиеся процессы (рисунок 2.9) на фазовой плоскости изобразятся в виде кривых (рисунок 2.9б), сходящихся к началу координат. Начало координат в этом случае называется устойчивым узлом.

Рисунок 2.9 Монотонно сходящийся процесс

Монотонный расходящийся процесс (рисунок 2.10) изобразится в виде фазовой траектории, удаляющейся от начала координат (рисунок 2.10б). Начало координат в этом случае называется неустойчивым узлом.

Рисунок 2.10 Монотонно расходящийся процесс

Периодический процесс (рисунок 2.11) изобразится на фазовой плоскости в виде замкнутой кривой (рисунок 2.11,б), называемой предельным циклом. Предельный цикл называется устойчивым, когда все близлежащие фазовые траектории сходятся извне и изнутри к предельному циклу (рисунок 2.12,а), и неустойчивым, когда траектории расходятся от предельного цикла (рисунок 2.12,б).

В первом случае в системе устанавливаются устойчивые периодические колебания, называемые автоколебаниями. Во второмслучае имеем неустойчивое периодическое решение. При этомо системе можно сказать, что онаустойчива вмалом, т. е. устойчива при малых начальных значениях отклонения и скорости ( и 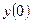), и неустойчива в большом, т. е. неустойчива при больших значениях и .

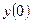Рисунок 2.11 Периодический процесс

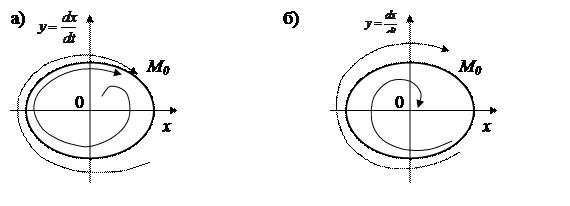
Рисунок 2.12 Фазовые траектории предельных циклов

В нелинейных системах зачастую одновременно имеется два предельных, цикла: малый – неустойчивый и большой – устойчивый (рисунок 2.13). При этом можно сказать, что система устойчива в малом, неустойчива в среднем и устойчива в большом. Внешний предельный цикл соответствует автоколебаниям в нелинейной системе.

Рисунок 2.13 Рисунок 2.14

Кроме особых линий типа предельного цикла, в нелинейных системах возможны и другие особые линии, как, например, особые линии типа отрезка (рисунок 2.14), характерные для систем с нелинейными звеньями, обладающими зоной нечувствительности.

Возможны также особые линии более сложного очертания.

Построение фазовых траекторий

При построении фазовых траекторий на фазовой плоскости 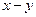надо принимать во внимание следующие общие правила их начертания:

1) На фазовой плоскости при скорость изменения равна нулю. Поэтому фазовые траектории пересекают ось 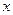под прямым углом.

2) При положительном значении , т.е. в верхней половине фазовой плоскости, изображающая точка движется слева направо, а при отрицательном значении , т.е. в нижней половине фазовой плоскости, наоборот, справа налево.

3) Фазовые траектории не пересекаются между собой, за исключением случаев пересечения в особых точках.

Строятся фазовые траектории по уравнению фазовой траектории 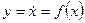, чтобы его получить сначала получают дифференциальное уравнение фазовой траектории из исходных дифференциальных уравнений системы:

(2.2)

исключая время посредством деления второго уравнения на первое.

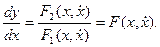(2.3)

В некоторых случаях это уравнение может быть проинтегрировано и найдено уравнение фазовой траектории , по которому строится фазовый портрет системы.

Для систем, содержащих звенья с кусочно-линейными характеристиками, на фазовой плоскости могут быть выделены области, в которых действуют уравнения (2.3) того или иного вида. Эти области разграничиваются так называемыми линиями переключения (рисунок 2.15).

Рисунок 2.15-Простейшие случаи расположения линий переключения

В тех случаях, когда уравнение (2.3) не интегрируется, можно использовать приближенный способ построения фазовых траекторий, называемый методом изоклин.

Литература 1осн [481-490]; 2осн [316-328]; 3осн [9-19], 6доп [178-187].

Контрольные вопросы

1 На какие две группы обычно делят методы исследования устойчивости нелинейных систем?

2 Дайте определение понятия изображающей точки.

3 Дайте определение понятия фазовой траектории.

4 Дайте определение понятия фазового пространства.

5 Какие особые точки и особые линии Вы знаете?

6 Перечислите общие правила начертания фазовых траекторий.

7 Что из себя представляют линии переключения на фазовой плоскости?

8 Что называется фазовым портретом системы?

9 Какое ограничение имеет метод фазовых траекторий?

Дата добавления: 2014-11-08