Производная и дифференциал

Производной функции 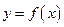называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

Производная функции имеет несколько обозначений: 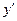, , 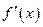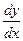. Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, .

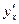Нахождение производной функции называется дифференцированием этой функции.

Таблица производных основных элементарных функций

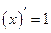
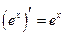
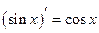
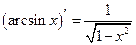
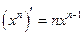
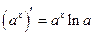
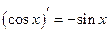
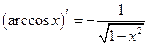
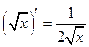
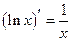
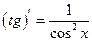
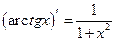
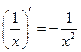
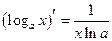
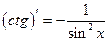
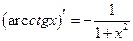
Пример 8.1. Найти производные функций: а) , б) .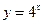

Решение.

а) – степенная функция. Используя формулу производной для степенной функции, получим .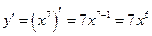

б) 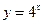– показательная функция. Используя формулу производной для показательной функции, получим .

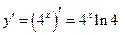Основные правила дифференцирования:

1. Производная постоянной равна нулю, т.е. .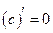

2. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е. .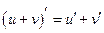

3. Производная произведения двух дифференцируемых функций равна произведению первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. .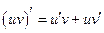

Следствие. Постоянный множитель можно выносить за знак производной .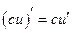

4. Производная частного двух дифференцируемых функций может быть найдена по формуле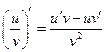

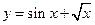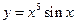Пример 8.2. Найти производные функций: а) , б) , в) .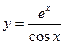

Решение.

а) По правилу дифференцирования суммы двух функций, получим .

б) По правилу дифференцирования произведения двух функций, получим .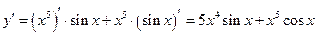

в) б) По правилу дифференцирования частного двух функций, получим .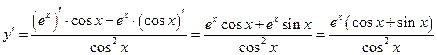

Пусть переменная 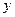есть функция от переменной 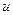, а переменная 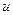в свою очередь есть функция от независимой переменной 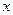, т.е. задана сложная функция .

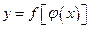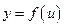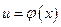Теорема. Если и – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной 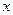, т.е. .

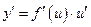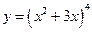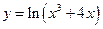Пример 8.3. Найти производные функций: а) , б) , в) .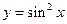

Решение.

а) Функцию 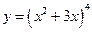можно представить в виде 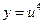, где 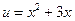, тогда .

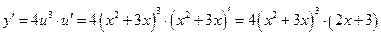б) Имеем 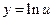, где 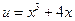, тогда .

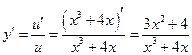в) Имеем 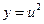, где 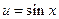, тогда .

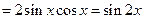Производная 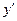сама является функцией, которая также может иметь производную. Производной 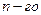порядка называется производная от производной 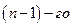порядка.

Пример 8.4. Найти производную второго порядка от функции .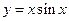

Решение. Дифференцируя данную функцию, получим 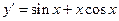. Дифференцируя производную 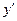, найдем вторую производную .

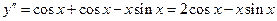Дифференциалом функции называется главная, линейная относительно 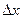часть приращения функции, равная произведению производной на приращение независимой переменной .

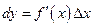Дифференциал независимой переменной равен приращению этой переменной. Поэтому формулу для дифференцирования функции можно записать в виде 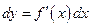, откуда .

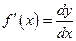Пример 8.5. Найти дифференциал функции .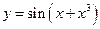

Решение. Дифференциал функции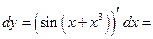

.

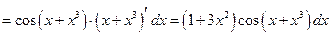Дифференциалом второго порядка (или вторым дифференциалом) 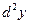функции 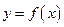называется дифференциал от дифференциала первого порядка этой функции, т.е. .

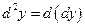Аналогичного дифференциалом 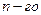порядка (или 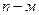дифференциалом) 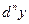называется дифференциал от дифференциала 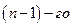порядка этой функции, т.е. .

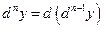Итак, по определению 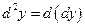. Найдем выражение второго дифференциала функции 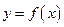. Так как не зависит от 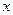, то при дифференцировании считаем 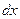постоянным: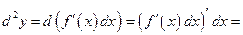 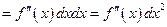, т.е. 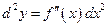. Аналогично, выражение 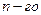дифференциала функции имеет вид .

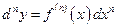Пример 8.6. Найти 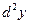, если .

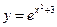Решение. Так как 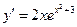, , 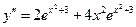то .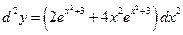

Дата добавления: 2014-11-25