
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускорение точки
|
|
|
|
Установлено, что ускорение 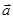 лежит в соприкасающейся плоскости, т. е. в плоско-
лежит в соприкасающейся плоскости, т. е. в плоско-
сти Mτn. Следовательно, проекция вектора 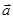 на бинормаль равна нулю (
на бинормаль равна нулю (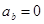 ). Найдем проекции
). Найдем проекции 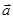 на две другие оси. Проектируя обе части равенства
на две другие оси. Проектируя обе части равенства  на оси Мτ и Мn и обозначая символами
на оси Мτ и Мn и обозначая символами 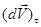 и
и  проекции вектора
проекции вектора 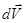 на эти оси получим:
на эти оси получим:

| (2.20) |

Рисунок 2.8
Вектор 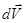 представляет собой разность между скоростями в двух соседних точках М и
представляет собой разность между скоростями в двух соседних точках М и  (рис. 123,Т), т.е.
(рис. 123,Т), т.е.  . Отложим векторы
. Отложим векторы  и
и  от общего начала (рис. 1.8), тогда
от общего начала (рис. 1.8), тогда 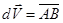 , а фигуру АСВD при бесконечно малом угле
, а фигуру АСВD при бесконечно малом угле 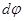 можно рассматривать как прямоугольник. Отсюда
можно рассматривать как прямоугольник. Отсюда 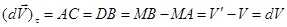 , где dV – элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можно АD рассматривать как элементарную дугу радиуса МА, размер которой определяется произведением радиуса на центральный угол. Тогда
, где dV – элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можно АD рассматривать как элементарную дугу радиуса МА, размер которой определяется произведением радиуса на центральный угол. Тогда 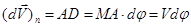 . Подставляя найденные значения
. Подставляя найденные значения 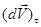 и
и  в формулы проекций
в формулы проекций  , получим:
, получим:
 . .
| (2.21) |
Угол между касательными к кривой в двух ее точках называется углом смежности, тогда 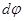 - элементарный угол смежности. Отношение
- элементарный угол смежности. Отношение 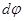 к dS =
к dS = 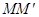 , определяет кривизну кривой в точке М, а кривизна k является величиной, обратной радиусу кривизны в этой точке, т.е.
, определяет кривизну кривой в точке М, а кривизна k является величиной, обратной радиусу кривизны в этой точке, т.е.
 . .
| (2.22) |
Введем эту величину в равенство 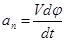 и преобразуем его, учтя, что
и преобразуем его, учтя, что  , к виду
, к виду
 . .
| (2.23) |
В результате окончательно получим:
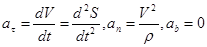
| (2.24) |
Таким образом, проекция ускорения точки на касательную равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) S по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю.
|
|
|
Это одна из важных теорем кинематики. Величины  и
и  называют касательным и нормальным ускорениями точки.
называют касательным и нормальным ускорениями точки.
При движении точки М в одной плоскости касательная Мτ поворачивается вокруг бинормали Mb с угловой скоростью 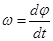 . Тогда
. Тогда 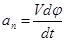 дает еще одну формулу для вычисления
дает еще одну формулу для вычисления  :
:
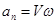 . .
| (2.25) |
Это значит, что нормальное ускорение равно произведению скорости точки на угловую скорость поворота касательной к траектории.
Кроме числового значения полного ускорения и его составляющих  и
и  важно знать их направление. Отложим вдоль касательной Мτ и главной нормали Mn векторы
важно знать их направление. Отложим вдоль касательной Мτ и главной нормали Mn векторы 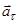 и
и  (рис.2.9). При этом составляющая
(рис.2.9). При этом составляющая  всегда направлена в сторону вогнутости кривой, так как всегда
всегда направлена в сторону вогнутости кривой, так как всегда  >0, а составляющая
>0, а составляющая 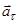 может быть направлена или в положительном, или в отрицательном направлении оси Мτ в зависимости от знака
может быть направлена или в положительном, или в отрицательном направлении оси Мτ в зависимости от знака  .
.
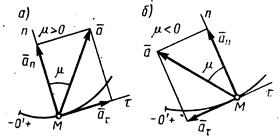
Рисунок 2.9
Вектор 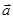 изображается диагональю параллелограмма, построенного на
изображается диагональю параллелограмма, построенного на 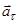 и
и  . Так как эти составляющие взаимно перпендикулярны, то модуль вектора
. Так как эти составляющие взаимно перпендикулярны, то модуль вектора 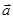 и угол µ его отклонения от нормали Mn определяется формулами:
и угол µ его отклонения от нормали Mn определяется формулами:
 , ,
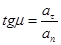 , ,
| (2.26) |
где -  ; при µ >0 вектор
; при µ >0 вектор 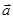 отклонен от нормали Mn в сторону оси Мτ, а при µ <0 – в противоположную сторону.
отклонен от нормали Mn в сторону оси Мτ, а при µ <0 – в противоположную сторону.
Таким образом, если движение точки задано естественным способом, то, зная траекторию (а, следовательно, и ее радиус кривизны в любой точке) и закон движения, т.е. зависимость 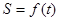 , можно определить модуль и направление векторов скорости и ускорения в любой момент времени.
, можно определить модуль и направление векторов скорости и ускорения в любой момент времени.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!