Опорные векторы

Определение 1. Вектор 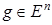называется опорным в точке ко множеству 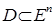, если выполняется неравенство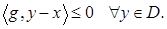

При этом для 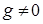гиперплоскость называется опорной в точке 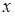ко множеству .

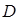Легко увидеть, что опорные векторы определяются не единственным образом. Обозначим через множество опорных векторов в точке 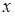ко множеству 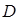. Иногда множество векторов опорных в 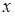к 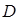будем обозначать .

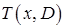Очевидно, что нулевой вектор всегда включается во множество , причем если 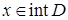, то . Далее в этом параграфе мы изучим условия существования ненулевых опорных векторов. Но прежде приведем следующее определение.

Определение 2. Вектор называется строго опорным в точке 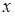ко множеству 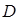, если выполняется неравенство .

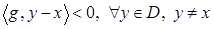Очевидно, что строго опорный вектор является опорным. Обратное утверждение, вообще говоря, неверно.

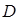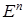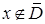Теорема 1. Пусть – выпуклое множество из и . Тогда существует вектор строго опорный в точке 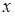ко множеству .

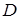Доказательство. Согласно теореме 7.2 существует проекция 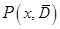. Обозначим для краткости 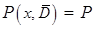и положим 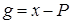. Так как 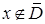, вектор 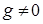. Убедимся, что вектор – строго опорный к 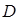в точке 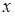. Согласно теореме 1.3 из выпуклости множества 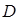следует выпуклость 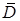. Тогда из теоремы 7.3 следует, что неравенство 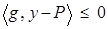справедливо для всех 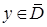, а значит, и для всех 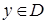. Преобразуем это неравенство следующим образом:

,

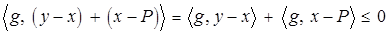откуда 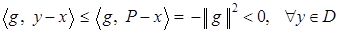. Что и требовалось.

Теорема 2. Пусть 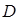– выпуклое множество и 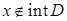. Тогда существует ненулевой опорный вектор в точке 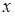ко множеству .

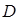Доказательство. Если 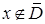, то этот факт следует из теоремы 1. Пусть 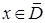. Тогда из условия теоремы следует, что 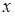– граничная точка множества 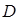. Поэтому существует последовательность такая, что 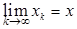. Соглас-

но теореме 1 для любого 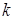существует ненулевой вектор 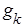строго опорный в точке 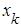ко множеству 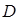. Следовательно, для всех 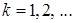имеем

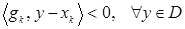. (1)

Не нарушая общности, можно считать, что для всех 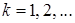Поэтому последовательность 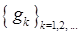имеет предельную точку. Так же без ограничения общности будем считать, что эта последовательность сходится. Положим 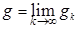. Очевидно, что 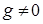. Перейдем в (1) к пределу по 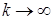. Получим 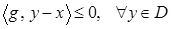. Таким образом, – опорный вектор в точке 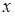ко множеству 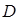. Что и требовалось.

Замечание. Ненулевой опорный вектор в точке 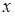ко множеству 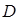является строго опорным вектором в 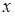ко множеству .

Дата добавления: 2014-11-25