Напряжение и деформация

Если на тело действуют внешние силы, то внутри него устанавливается уравновешенная система внутренних сил.

На­пряжение представляет собой меру интенсивности, с которой действуют эти сбалансированные внутренние силы.

Напряже­ние, действующее на некоторую площадку любой поверхности внутри тела, можно разложить на две компоненты: нормальное напряжение, направленное перпендикулярно этой площадке, и сдвиговое, лежащее в плоскости площадки.

В любой точке находящегося в напряженном состоянии тела можно выделить три ортогональные плоскости, на которых на­пряжения полностью являются нормальными, т. е. вдоль них не действуют сдвиговые напряжения. Эти плоскости определяют три ортогональные оси, называемые главными осями напряже­ний, а нормальные напряжения, действующие в этих направ­лениях, называются главными напряжениями. Каждое главное напряжение отражает равновесие равных, но противоположно направленных компонент сил. Напряжение считается сжимаю­щим, если силы направлены навстречу друг другу, и растяги­вающим, если они направлены в противоположные стороны.

Если внутри тела все главные напряжения равны по вели­чине, то режим напряжений называют гидростатическим, по­скольку таким является напряженное состояние всего объема жидкости, находящегося в покое. В гидростатическом поле на­пряжений не существует сдвиговых напряжений, так как они не могут поддерживаться в жидком теле.

Если главные напряжения не равны, сдвиговые напряжения действуют вдоль всех поверхностей внутри напряженного тела, за исключением трех ортогональных плоскостей, пересекающихся по главным осям.

Тело, подвергающееся действию напряжений, испытывает изменение формы и (или) размеров, называемое деформацией. Вплоть до некоторого предельного значения напряжения, на­зываемого пределом текучести материала, величина деформа­ции изменяется пропорционально приложенному напряжению (закон Гука). Эта упругая деформация является обратимой, т.е. снятие напряжения ведет к снятию деформации. Если напряжение превысит предел текучести, деформация становит­ся нелинейной и частично необратимой (т.е. возникает оста­точная деформация) и называется она пластической деформацией. Если напряжение возрастает еще больше, тело разрушается. Типичная кривая зависимости деформации от напряжения по­казана на рис.1.

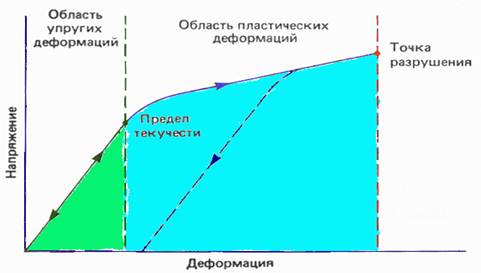
Рис. 1.Типичная зависимость между напряжением и деформацией

в твер­дом теле.

Конкретный вид линейного соотношения между напряжени­ем и деформацией в упругой области определяется для любого вещества характерными для него модулями упругости, каж­дый из которых представляет собой отношение какого-либо вида напряжения к, возникающей в результате его действия, деформации.

Рассмотрим стержень, первоначальная длина ко­торого l, а площадь поперечного сечения А. Под действием рас­тягивающей силы F,приложенной к торцам стержня, его длина увеличивается на 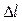(рис.2, а). Этот процесс характеризуется модулем Юнга (Е), определяемым следующим образом:

.

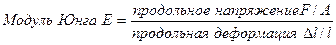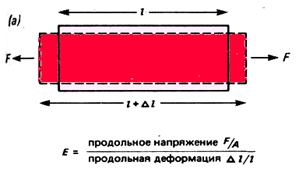
Рис. 2. Модули упругости: (а) – модуль Юнга Е;(б) – объемный модуль К;(в) – модуль сдвига µ; (г) – модуль продольной деформации j.

Заметим, что растяжение такого стержня будет сопровож­даться сокращением его диаметра, т. е. стержень будет испы­тывать не только продольную, но и поперечную деформацию.

Отношение поперечной деформации к продольной называется коэффициентом Пуассона .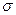

Объемный модуль упругости К выражает отношение напря­жения к деформации в случае, когда к кубику вещества при­ложено простое гидростатическое давление Р (рис.2, б);. воз­никающая при этом объемная деформация равна величине из­менения объема 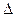v, деленной на первоначальный объем v:

.

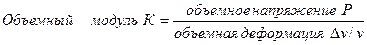Рис. 2. Модули упругости: (а) – модуль Юнга Е;(б) – объемный модуль К;(в) – модуль сдвига µ; (г) – модуль продольной деформации j.

Аналогичным образом модуль сдвига µ, определяется как отношение сдвигового напряжения τ к соответствующей сдви­говой деформации tgО (рис.2, в):

Рис. 2. Модули упругости: (а) – модуль Юнга Е;(б) – объемный модуль К; (в) – модуль сдвига µ; (г) – модуль продольной деформации j.

Наконец, модуль продольной деформации j представляет собой отношение продольного напряжения к продольной де­формации при отсутствии поперечной деформации, т. е. когда материал может деформироваться только одноосно (рис.2, г):

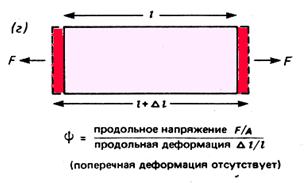
Рис. 2. Модули упругости: (а) – модуль Юнга Е; (б) – объемный модуль К;(в) – модуль сдвига µ; (г) – модуль продольной деформации j.

Численные научные и инженерные разработки нашего столетия позволи­ли получить полную картину строения Земли, какой мы ее знаем сегод­ня. Благодаря совместным усилиям и профессиональным способностям сейсмологов, геологов, океанологов, геодезистов, биологов, антрополо­гов, археологов, инженеров-электронщиков была получена эта картина.

Рис. 2. Модули упругости: (а) – модуль Юнга Е; (б) – объемный модуль К;(в) – модуль сдвига µ; (г) – модуль продольной деформации j.

Дата добавления: 2014-11-25