
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скалярное произведение векторов
|
|
|
|
С.Д. Барышников «Лекции по анатомии и физиологии человека с основами патологии». Москва, 2002.
Определение 1.5.1. Пусть 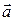 и
и  – произвольные векторы. Скалярным произведением вектора
– произвольные векторы. Скалярным произведением вектора 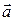 на вектор
на вектор  называется число (скаляр), которое обозначается
называется число (скаляр), которое обозначается  и определяется следующим образом:
и определяется следующим образом:

Скалярный квадрат вектора  т.е. неотрицательное число
т.е. неотрицательное число  будем обозначать
будем обозначать 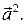 Из определения вытекают следующие формулы для вычисления длины произвольного вектора
Из определения вытекают следующие формулы для вычисления длины произвольного вектора 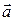 и величины угла между ненулевыми векторами
и величины угла между ненулевыми векторами 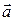 и
и  через скалярное произведение:
через скалярное произведение:
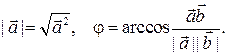 (1)
(1)
Приведем далее утверждение технического характера, оно понадобится нам при доказательстве одного из свойств скалярного произведения.
Лемма 1.5.1. Пусть 
 – прямая с направляющим вектором
– прямая с направляющим вектором 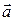 ,
,  – базисный вектор единичной длины множества
– базисный вектор единичной длины множества 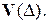 Тогда число
Тогда число 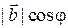 есть координата ортогональной проекции
есть координата ортогональной проекции 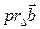 вектора
вектора  на прямую
на прямую  в базисе
в базисе  .
.
Доказательство. Отложим от точки  вектор
вектор  получим точку В. Пусть
получим точку В. Пусть  – ортогональная проекция точки В на прямую
– ортогональная проекция точки В на прямую  (рис. 5.1).
(рис. 5.1).

Рис. 5.1
Тогда вектор 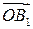 есть ортогональная проекция
есть ортогональная проекция 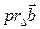 вектора
вектора  на прямую
на прямую  Пусть
Пусть 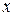 – координата вектора
– координата вектора 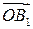 в единичном базисе
в единичном базисе  В § 1.3 отмечалось, что
В § 1.3 отмечалось, что 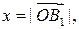 если векторы
если векторы 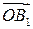 и
и  сонаправлены, и
сонаправлены, и  если векторы
если векторы 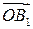 и
и  противоположно направлены. Заметим, что в обоих случаях
противоположно направлены. Заметим, что в обоих случаях 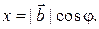 Действительно, если
Действительно, если 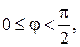 то
то  и
и  если же
если же  то
то 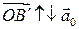 и
и 
Следующее утверждение описывает основные свойства скалярного произведения, в частности, показывает, как скалярное произведение связано с операциями сложения векторов и умножения векторов на числа.
Утверждение 1.5.1. Для любых векторов 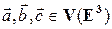 и любого числа
и любого числа  верны следующие равенства:
верны следующие равенства:
(i)  – свойство коммутативности скалярного произведения;
– свойство коммутативности скалярного произведения;
(ii) 
(iii) 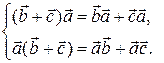
Справедливость равенств (ii) и (iii) означает, что скалярное произведение билинейно.
|
|
|
(iv) 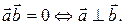
Свойство (iv) означает, что равенство нулю скалярного произведения двух векторов является критерием их ортогональности.
Доказательство. (i) Коммутативность скалярного произведения вытекает непосредственно из определения.
(ii) Все три числа 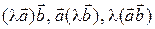 равны нулю, если хотя бы один из векторов нулевой или
равны нулю, если хотя бы один из векторов нулевой или 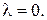 Если же векторы ненулевые и
Если же векторы ненулевые и  то каждое из трех указанных выше чисел равно
то каждое из трех указанных выше чисел равно 
(iii) В силу коммутативности скалярного произведения достаточно доказать справедливость первого из двух равенств в (iii). Если хотя бы один из трех векторов 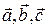 нулевой или
нулевой или  то равенство, очевидно, верно. Пусть
то равенство, очевидно, верно. Пусть  – ненулевые векторы. Пусть
– ненулевые векторы. Пусть 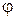 – величина угла между векторами
– величина угла между векторами 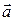 и
и  ,
,  – величина угла между векторами
– величина угла между векторами 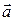 и
и 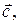
 – величина угла между векторами
– величина угла между векторами 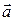 и
и 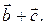 Отложим от некоторой точки О вектор
Отложим от некоторой точки О вектор 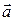 . Получим точку А, отличную от О. Обозначим
. Получим точку А, отличную от О. Обозначим  прямую, проходящую через O и А. В силу леммы 5.1, имеем:
прямую, проходящую через O и А. В силу леммы 5.1, имеем:

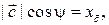
 –
–
координаты ортогональных проекций 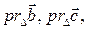
 векторов
векторов  на прямую
на прямую  в базисе
в базисе 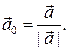 Теперь, используя вначале утверждение 1.4.1 о том, что проекция суммы векторов равна сумме проекций, а затем следствие 1.4.1 о том, что координата суммы векторов равна сумме координат, получаем, что
Теперь, используя вначале утверждение 1.4.1 о том, что проекция суммы векторов равна сумме проекций, а затем следствие 1.4.1 о том, что координата суммы векторов равна сумме координат, получаем, что

Умножив обе части последнего равенства на число 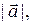 имеем:
имеем:
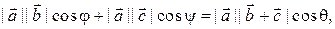
т.е. 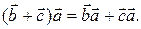
(iv) Если 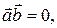 то выполняется хотя бы одно из условий:
то выполняется хотя бы одно из условий:
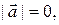 или
или 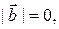 или
или 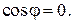
Из каждого условия следует ортогональность векторов 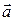 и
и  . Обратно, если
. Обратно, если 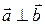 , то хотя бы один из векторов нулевой, или
, то хотя бы один из векторов нулевой, или 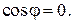 Следовательно,
Следовательно, 
Пусть векторы  и
и 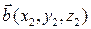 заданы своими координатами в некотором базисе
заданы своими координатами в некотором базисе 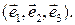 Пользуясь билинейностью, скалярное произведение
Пользуясь билинейностью, скалярное произведение  можно выразить через скалярные произведения базисных векторов:
можно выразить через скалярные произведения базисных векторов:
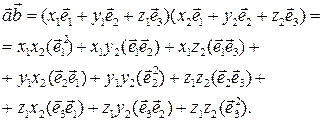 (2)
(2)
Построим таблицу умножения (скалярного) базисных векторов:
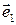
| 
| 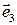
| |
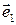
| 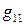
| 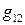
| 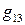
|

| 
| 
| 
|
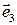
| 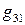
| 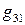
| 
|
В этой таблице число 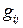 обозначает скалярное произведение
обозначает скалярное произведение  В силу свойств скалярного произведения имеем:
В силу свойств скалярного произведения имеем:  Теперь скалярное произведение (2) векторов
Теперь скалярное произведение (2) векторов 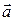 и
и  коротко можно записать в виде
коротко можно записать в виде
|
|
|
 (3)
(3)
Удобно использовать также матричные обозначения. Пусть
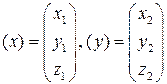 – координатные столбцы векторов
– координатные столбцы векторов 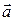 и
и  ;
;
 – матрица попарных скалярных произведений базисных векторов. Матрица
– матрица попарных скалярных произведений базисных векторов. Матрица  называется матрицей скалярного произведения в базисе
называется матрицей скалярного произведения в базисе 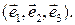 Равенство (3) теперь записывается в виде:
Равенство (3) теперь записывается в виде:
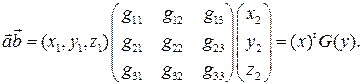
Наиболее простой вид формула (3) принимает, если векторы заданы своими координатами в ортонормированном базисе. Действительно, пусть  – ортонормированный базис. Тогда скалярные квадраты базисных векторов равны 1, а попарные произведения различных базисных векторов равны 0, т.е.
– ортонормированный базис. Тогда скалярные квадраты базисных векторов равны 1, а попарные произведения различных базисных векторов равны 0, т.е.

Таким образом, матрица скалярного произведения в ортонормированном базисе – единичная. В этом случае скалярное произведение векторов вычисляется по формуле:

а формулы (1) для длины вектора и величины угла между векторами имеют вид:
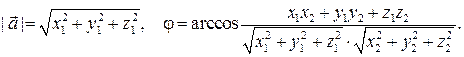 (
(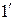 )
)
Если векторы 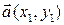 и
и 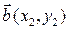 заданы своими координатами в ортонормированном базисе
заданы своими координатами в ортонормированном базисе 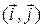 плоскости, то получаем аналоги формул (
плоскости, то получаем аналоги формул (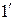 ):
):
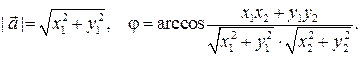 (4)
(4)
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 472; Нарушение авторских прав?; Мы поможем в написании вашей работы!