
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сухопутные войска 3 страница
3.5. Обобщенный метод наименьших квадратов (ОМНК)
Из-за неэффективности оценок, полученных методом наименьших квадратов (МНК) при наличии гетероскедастичности, используется обобщенный (взвешенный) метод наименьших квадратов (ОМНК). В этом методе вклад данных наблюдений, имеющих большую дисперсию, уменьшается.
В качестве примера рассмотрим теоретическую линейную регрессионную модель с двумя переменными:
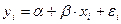 ,
,
где:
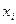 – объясняющая (независимая) переменная – неслучайная величина;
– объясняющая (независимая) переменная – неслучайная величина;
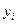 - объясняемая (зависимая) переменная;
- объясняемая (зависимая) переменная;
 – случайное слагаемое (ошибка регрессии);
– случайное слагаемое (ошибка регрессии);
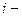 порядковый номер наблюдения за реализацией событий;
порядковый номер наблюдения за реализацией событий;
α и β – параметры уравнения.
Предположим, что в исходной модели регрессии случайные слагаемые гетероскедастичны, что исключает постоянство значений дисперсии ошибок  . Если дисперсии
. Если дисперсии  в каждом наблюдении известны, то, разделив каждое слагаемое в линейной регрессионной модели на соответствующее ему значение
в каждом наблюдении известны, то, разделив каждое слагаемое в линейной регрессионной модели на соответствующее ему значение  , можно получить преобразованную модель:
, можно получить преобразованную модель:
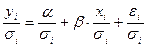 .
.
Для этой модели условие гомоскедастичности выполняется, и потому можно оценить обычным МНК параметры преобразованного уравнения, а затем и параметры исходного уравнения методом ОМНК. Для каждого из этих методов необходима минимизация суммы квадратов отклонений, в процессе которой отдельные слагаемые этой суммы взвешиваются: наблюдениям с большей дисперсией придается меньший вес. Тем самым оценки исходной модели получают непосредственно по оценкам МНК коэффициентов преобразованной модели.
Как правило, на практике дисперсии  неизвестны, поэтому их заменяют какими-либо оценками. Для экономических данных дисперсии
неизвестны, поэтому их заменяют какими-либо оценками. Для экономических данных дисперсии  часто оказываются пропорциональными значениям объясняющей переменной
часто оказываются пропорциональными значениям объясняющей переменной 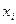 , что позволяет с помощью обычного МНК оценить параметры преобразованной модели:
, что позволяет с помощью обычного МНК оценить параметры преобразованной модели:
 .
.
В этом уравнении коэффициент при 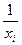 будет эффективной оценкой
будет эффективной оценкой  , а постоянное слагаемое – эффективной оценкой
, а постоянное слагаемое – эффективной оценкой  .
.
ОМНК обеспечивает не только несмещенность оценок параметров, но и меньшую дисперсию по сравнению с теми оценками, которые получены при минимизации суммы квадратов без взвешивания отдельных слагаемых.
3.6. Выявление автокорреляции
Одной из самых важных предпосылок регрессионного анализа является независимость случайной слагаемой уравнения регрессии в любом наблюдении от его значений во всех других наблюдениях. Если это условие не выполняется, то говорят, что случайное слагаемое подвержено автокорреляции. При этом коэффициенты регрессии, получаемые методом наименьших квадратов (МНК), оказываются неэффективными, хотя и несмещенными, а их стандартные ошибки занижаются.
Обычно автокорреляция появляется при исследовании данных временных рядов. Возникновение автокорреляции обычно связано с тем, что:
1) либо случайная составляющая уравнения регрессии подвергается воздействию некоторого постоянно действующего фактора, не включаемого в модель;
2) либо текущее значение случайной составляющей коррелированно с ее предыдущими значениями. Поэтому можно ожидать, что при работе с набором одновременных наблюдений явление автокорреляции будет наблюдаться достаточно редко.
Пусть, например, обследуется выборка, состоящая из различных фирм, отраслей промышленности и т.д. Скорее всего, вероятность того, что при таком обследовании значение одной из переменных, заданной для какого-либо объекта, окажется связанной с зафиксированным значением этой же переменной другого объекта, очень мала. С другой стороны, циклический характер переменных приводит к тому, что при работе с временными рядами явление автокорреляции встречается довольно редко.
Необходимым условием независимости случайных слагаемых является их некоррелированность для каждых двух соседних значений. При этом корреляция между соседними случайными слагаемыми уравнения регрессии оценивается коэффициентом корреляции 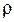 между ними.
между ними.
Но значения этих случайных слагаемых обычно на практике неизвестны, поэтому проверяется статистическая некоррелированность остатков 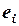 и
и  разностей между измеренными значениями объясняемой переменной и расчетными значениями, определяемыми из уравнения регрессии, полученного с использованием обычного МНК. Такой оценкой коэффициента корреляции является коэффициент автокорреляции остатков первого порядка, который имеет вид:
разностей между измеренными значениями объясняемой переменной и расчетными значениями, определяемыми из уравнения регрессии, полученного с использованием обычного МНК. Такой оценкой коэффициента корреляции является коэффициент автокорреляции остатков первого порядка, который имеет вид:
 ,
,
где  и
и 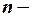 порядковый номер и общее число наблюдений.
порядковый номер и общее число наблюдений.
При выявлении автокорреляции выдвигается гипотеза  (об отсутствии корреляции первого порядка). Для проверки гипотезы используют статистику Дарбина-Уотсона, рассчитываемую по формуле:
(об отсутствии корреляции первого порядка). Для проверки гипотезы используют статистику Дарбина-Уотсона, рассчитываемую по формуле:

 .
.
Еслиавтокорреляция остатков отсутствует ( ), то
), то  . При положительной автокорреляции (
. При положительной автокорреляции (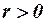 ) имеем
) имеем  . При отрицательной автокорреляции (
. При отрицательной автокорреляции (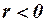 ) ―
) ― 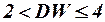 .
.
По таблице определяют критические (пороговые) значения критерия Дарбина-Уотсона 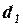 и
и  для заданного числа наблюдений, числа объясняющих переменных и уровня значимости. По этим значениям интервал (0;4) разбивается на 5 зон, и в зависимости от того, в какую зону попадает расчетное значение критерия, принимают или отвергают соответствующую гипотезу:
для заданного числа наблюдений, числа объясняющих переменных и уровня значимости. По этим значениям интервал (0;4) разбивается на 5 зон, и в зависимости от того, в какую зону попадает расчетное значение критерия, принимают или отвергают соответствующую гипотезу:
| Номер зоны | Диапазон изменения статистики | Вывод о наличии автокорреляции |
| (0;d1) | гипотеза H0 отвергается (положительная автокорреляция) | |
| (d1;d2) | зона неопределенности | |
| (d2;4- d2) | гипотеза H0 принимается (отсутствие автокорреляции) | |
| (4- d2;4- d1) | зона неопределенности | |
| (4- d1;4) | гипотеза H0 отвергается (отрицательная автокорреляция) |
Наличие зон неопределенности связано с тем, что распределение  статистики зависит не только от числа объясняющих переменных, но и от значений объясняющих переменных.
статистики зависит не только от числа объясняющих переменных, но и от значений объясняющих переменных.
3.7 Оценивание параметров уравнения регрессии при автокорреляции
Пусть исходное равнение регрессии, содержащее автокорреляцию случайных слагаемых, имеет вид:
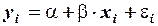 ,
,
где:
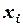 – объясняющая (независимая) переменная – неслучайная величина;
– объясняющая (независимая) переменная – неслучайная величина;
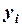 – объясняемая (зависимая) переменная;
– объясняемая (зависимая) переменная;
 – случайное слагаемое (ошибка регрессии);
– случайное слагаемое (ошибка регрессии);
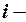 порядковый номер наблюдения за реализацией событий;
порядковый номер наблюдения за реализацией событий;
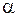 и
и 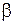 – параметры уравнения.
– параметры уравнения.
Пусть автокорреляция подчиняется автокорреляционной схеме первого порядка:
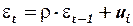 ,
,
где:
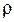 – коэффициент автокорреляции;
– коэффициент автокорреляции;
 случайное слагаемое, удовлетворяющее предпосылкам, определяющим возможность применения методом наименьших квадратов (МНК).
случайное слагаемое, удовлетворяющее предпосылкам, определяющим возможность применения методом наименьших квадратов (МНК).
Данная схема называется авторегрессионной, поскольку 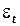 определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно 1. Величина
определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно 1. Величина 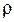 представляет собой коэффициент корреляции между двумя соседними ошибками.
представляет собой коэффициент корреляции между двумя соседними ошибками.
Предположим, что 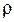 известно. Преобразуем исходное уравнение регрессии следующим образом:
известно. Преобразуем исходное уравнение регрессии следующим образом:
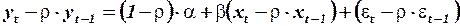 .
.
Обозначим: 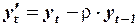 ,
,  .
.
Это преобразование переменных называется авторегрессионным или преобразованием Бокса-Дженкинса.
Преобразованное уравнение будет иметь вид:
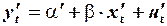 ,
,
где переменная 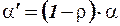 – не содержит автокорреляцию; при этом для оценки параметров
– не содержит автокорреляцию; при этом для оценки параметров 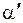 и
и 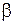 используется обычный МНК.
используется обычный МНК.
Теперь коэффициент 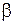 оценивается непосредственно, а коэффициент
оценивается непосредственно, а коэффициент 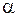 рассчитывается по формуле
рассчитывается по формуле 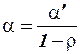 .
.
На практике величина 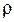 неизвестна, ее оценка получается одновременно с оценками
неизвестна, ее оценка получается одновременно с оценками 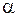 и
и 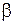 в результате различных итеративных процедур (например, процедура Хильдрата-Лу).
в результате различных итеративных процедур (например, процедура Хильдрата-Лу).
Процедура Хильдрата-Лу. Эта процедура, широко применяемая в регрессионных пакетах, основана на использовании следующего алгоритма:
1) преобразованное уравнение оценивается для каждого значения 
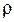 из интервала (-1,1] с заданным шагом внутри него;
из интервала (-1,1] с заданным шагом внутри него;
2) выбирается то значение ρ, для которого сумма квадратов остатков в преобразованном уравнении минимальна, а коэффициенты регрессии определяются при оценивании преобразованного уравнения с использованием этого значения.
ГЛАВА 4. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
4.1. Структурная форма уравнений
Структурная форма модели (системы одновременных уравнений) – это система уравнений, в каждом из которых помимо объясняющих (независимых) переменных могут содержаться объясняемые (зависимые) переменные из других уравнений. Уравнения, составляющие исходную модель, называются структурными уравнениями модели.
Простейшая структурная форма модели имеет вид:
 ,
,
 ,
,
где:
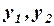 и
и  зависимые и независимые переменные;
зависимые и независимые переменные;
 и
и 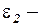 случайные слагаемые;
случайные слагаемые;
 параметры модели.
параметры модели.
Параметры структурной формы модели называются структурными коэффициентами.
Структурная форма модели включает в систему не только уравнение, отражающее взаимосвязи между отдельными переменными, но и уравнения, отражающие тенденцию развития явления – функции времени, а также разного рода уравнения-тождества. Тождества не содержат каких-либо подлежащих оценке параметров, а также не включают случайных слагаемых.
В процессе оценивания параметров одновременных уравнений следует различать эндогенные (внутренние, зависимые) и экзогенные переменные. Эндогенными считаются переменные, значения которых определяются внутри модели. Это зависимые переменные, число которых равно числу уравнений системы. Экзогенными (внешними, независимыми) считаются переменные, значения которых определяются вне модели. Это заданные переменные, влияющие на эндогенные переменные, но не зависящие от них.
В качестве экзогенных могут рассматриваться значения эндогенных переменных за предшествующий период времени.
Обычно в каждом уравнении предполагается отсутствие корреляции экзогенных переменных со случайной составляющей. Однако в общем случае может иметь место корреляция эндогенных переменных со случайной составляющей, из-за которой использование метода МНК приводит к несостоятельным оценкам структурных коэффициентов. Поэтому для определения этих коэффициентов структурные уравнения модели преобразуют в приведенную форму.
4.2. Приведенная форма уравнений
Приведенной формой уравнений называется система уравнений, в каждом из которых эндогенные переменные выражены только через экзогенные переменные и случайные составляющие. Уравнения, составляющие исходную модель, называют структурными уравнениями модели.
Приведенная форма простейшей исходной модели имеет вид:
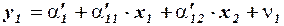 ,
,
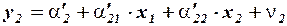 ,
,
где:
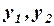 и
и  зависимые и независимые переменные;
зависимые и независимые переменные;
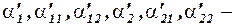 параметры приведенной формы модели;
параметры приведенной формы модели;
 и
и 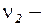 случайные слагаемые.
случайные слагаемые.
Параметры – коэффициенты приведенной формы модели системы уравнений называются коэффициенты приведенной формы (приведенными коэффициентами). Они оцениваются обычным методом наименьших квадратов (МНК), поскольку экзогенные переменные не коррелированны со случайными слагаемыми.
Рассчитанные коэффициенты приведенной формы могут быть использованы для оценивания структурных коэффициентов. Такой способ оценивания структурных коэффициентов называется косвенным методом наименьших квадратов (КМНК).
Структурные коэффициенты можно однозначно выражать через приведенные коэффициенты, или они могут иметь несколько разных оценок, но совсем не выражаться через них.
Структурный коэффициент называется идентифицируемым, если его можно точно вычислить на основе приведенных коэффициентов, точно идентифицируемым, если он имеет единственную оценку, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.
С труктурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель является неидентифицируемой.
В зависимости от вида системы одновременных уравнений коэффициенты структурной модели могут быть оценены различными способами. Наиболее распространены следующие методы:
· метод инструментальных переменных (ИП);
· косвенный метод наименьших квадратов (КМНК);
· двухшаговый метод наименьших квадратов (ДМНК).
4.3. Случай идентифицируемости: косвенный метод наименьших квадратов и метод инструментальных переменных
Предположим, что необходимо оценить параметры уравнения функции потребления в простой модели Кейнса формирования доходов:
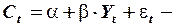 функция потребления,
функция потребления,
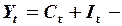 тождество доходов,
тождество доходов,
где:
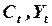 и
и  объем потребления, совокупный доход и инвестиции соответственно;
объем потребления, совокупный доход и инвестиции соответственно;
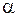 и
и 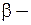 структурные коэффициенты, причем
структурные коэффициенты, причем 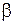 характеризует предельную склонность к потреблению;
характеризует предельную склонность к потреблению;
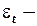 случайное слагаемое.
случайное слагаемое.
В исходной модели 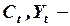 эндогенные (внутренние, зависимые) переменные,
эндогенные (внутренние, зависимые) переменные,  экзогенная – внешняя, независимая переменная. Непосредственное оценивание параметров
экзогенная – внешняя, независимая переменная. Непосредственное оценивание параметров 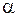 и
и 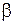 в структурном уравнении функции потребления дает смещенные и несостоятельные оценки, так как объясняющая переменная
в структурном уравнении функции потребления дает смещенные и несостоятельные оценки, так как объясняющая переменная  является эндогенной зависимой переменной. Разрешая структурную систему относительно эндогенных переменных, можно получить приведенную систему уравнений:
является эндогенной зависимой переменной. Разрешая структурную систему относительно эндогенных переменных, можно получить приведенную систему уравнений:

 ,
,
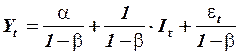 .
.
В приведенной системе уравнений коэффициенты при переменной  , равные
, равные 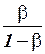 и
и  , представляют собой инвестиционные мультипликаторы потребления и дохода соответственно. Они показывают: если объем инвестиций возрастает на 1, то объем потребления увеличится на
, представляют собой инвестиционные мультипликаторы потребления и дохода соответственно. Они показывают: если объем инвестиций возрастает на 1, то объем потребления увеличится на 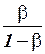 , а совокупный доход возрастет на
, а совокупный доход возрастет на  .
.
Известны разные методы оценивания структурных коэффициентов 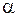 и
и 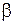 .
.
Косвенный метод наименьших квадратов ( КМНК ). Уравнение для  в приведенной форме имеет вид:
в приведенной форме имеет вид:
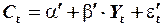 ,
,
где  .
.
Уравнение в приведенной форме включает экзогенную переменную  , которая некоррелирована со случайным слагаемым
, которая некоррелирована со случайным слагаемым 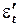 , поэтому для оценки параметров
, поэтому для оценки параметров 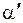 и
и 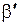 можно использовать обычный метод наименьших квадратов.
можно использовать обычный метод наименьших квадратов.
Оцененное с помощью МНК уравнение в приведенной форме, полученное по выборочным данным, будет иметь вид:
 ,
,
где  и
и  оценки параметров
оценки параметров 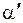 и
и 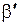 .
.
Полученные таким образом оценки будут представлять собой несмещенные и состоятельные оценки параметров 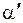 и
и 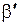 .
.
Используя приведенные выше соотношения параметров исходной (структурной) системы уравнений и приведенной системы уравнений, можно получить оценки параметров структурной системы уравнений:
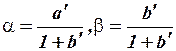 .
.
Поскольку получены единственные оценки 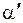 и
и 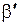 структурных коэффициентов через оценки
структурных коэффициентов через оценки  и
и  приведенных коэффициентов, то структурное уравнение функции потребления является однозначно определенным – точно идентифицируемым.
приведенных коэффициентов, то структурное уравнение функции потребления является однозначно определенным – точно идентифицируемым.
Проблема коррелированности объясняющей переменной  со случайным слагаемым
со случайным слагаемым 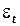 в структурном уравнении для
в структурном уравнении для  может быть разрешена с помощью метода инструментальных переменных. Для применения этого метода необходимо найти такую инструментальную переменную, которая обладает следующими свойствами:
может быть разрешена с помощью метода инструментальных переменных. Для применения этого метода необходимо найти такую инструментальную переменную, которая обладает следующими свойствами:
1) коррелируется с неудачно объясняющей переменной  ;
;
2) не коррелируется со случайным слагаемым 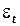 .
.
В рассматриваемом примере в качестве инструментальной переменной может быть использована величина  . Она коррелированна с
. Она коррелированна с  , так как
, так как  зависит от
зависит от  (что следует из исходных уравнений), и не коррелируется с
(что следует из исходных уравнений), и не коррелируется с 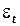 , поскольку является экзогенной (внешней) переменной.
, поскольку является экзогенной (внешней) переменной.
4.4. Случай сверхидентифицируемости: метод инструментальных переменных и двухшаговый метод наименьших квадратов (ДМНК)
Случай сверхидентифицируемой системы уравнений рассмотрим на примере модели формирования доходов Кейнса:
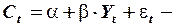 функция потребления,
функция потребления,
 тождество доходов,
тождество доходов,
где:
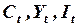 и
и  объем потребления, совокупный доход, инвестиции и государственные расходы соответственно;
объем потребления, совокупный доход, инвестиции и государственные расходы соответственно;
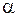 и
и 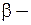 структурные коэффициенты, причем
структурные коэффициенты, причем 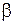 характеризует предельную склонность к потреблению;
характеризует предельную склонность к потреблению;
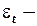 случайное слагаемое.
случайное слагаемое.
В исходной модели 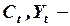 эндогенные переменные,
эндогенные переменные,  и
и  экзогенные.
экзогенные.
Разрешая структурную систему относительно эндогенных переменных, получим приведенную систему уравнений вида:
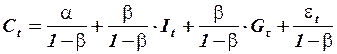 ,
,
 .
.
Для оценивания структурных коэффициентов 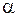 и
и 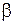 используются различные методы.
используются различные методы.
Метод инструментальных переменных. В структурном уравнениифункции потребления в качестве инструментальных переменных для  можно использовать
можно использовать  или
или  . В зависимости от выбора инструментальной переменной полученные оценки
. В зависимости от выбора инструментальной переменной полученные оценки 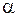 и
и 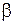 будут различаться, но в обоих случаях они будут состоятельными. Поэтому в данном случае в качестве инструментальной переменной наиболее целесообразно выбрать комбинацию
будут различаться, но в обоих случаях они будут состоятельными. Поэтому в данном случае в качестве инструментальной переменной наиболее целесообразно выбрать комбинацию  и
и  .
.
Структурное уравнение с избыточным числом экзогенных переменных, которые можно использовать как инструментальные, является переопределенным (сверхидентифицируемым).
Двухшаговый метод наименьших квадратов (ДМНК). Двухшаговый МНК можно рассматривать как частный случай конструирования наилучшей из возможных комбинаций инструментальных переменных, если в качестве последних использовать избыточные экзогенные переменные, имеющиеся в уравнении. Выше было отмечено, что при использовании метода инструментальных переменных структурное уравнениефункции потребления оказывается переопределенным, и потому для определения функции  выбирается линейная комбинация двух переменных
выбирается линейная комбинация двух переменных  и
и  :
:
|
|
Дата добавления: 2014-11-09; Просмотров: 350; Нарушение авторских прав?; Мы поможем в написании вашей работы!