
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення. Якби деяка паросполучення мала б дуг, то вона не відображала б у менш чим
|
|
|
|
Доведення.
Якби деяка паросполучення 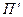 мала б
мала б 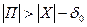 дуг, то вона не відображала б у
дуг, то вона не відображала б у 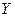 менш чим
менш чим 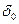 вершин з
вершин з 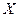 . Виходить, для кожного
. Виходить, для кожного 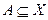 було б
було б  , що суперечить визначенню дефіциту.
, що суперечить визначенню дефіциту.
Позначимо через 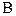 множину всіх таких підмножин
множину всіх таких підмножин 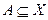 , для яких
, для яких 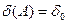 . Для посилення теореми нам знадобляться наступні властивості функціонала
. Для посилення теореми нам знадобляться наступні властивості функціонала 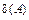 й множини
й множини  .
.
Твердження:
1. 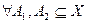
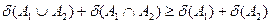 .
.
2. Якщо 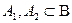 , то
, то 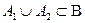 й
й 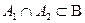 .
.
3. Нехай  . Якщо
. Якщо 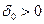 , то
, то 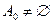 й
й 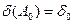 .
.
1. Властивість 1 одержимо, віднімаючи зі співвідношення
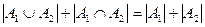
співвідношення

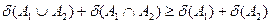 .
.
2. Якщо 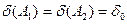 , то властивості 1.
, то властивості 1.

Далі,
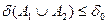 і
і 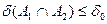 ,
, 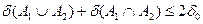 ,
,
отже,
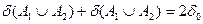
 і
і 
3. Припустимо 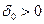 .
.
1) Тому що  - скінчено (адже
- скінчено (адже 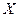 скінчено
скінчено  - скінчено), то по властивості 2
- скінчено), то по властивості 2 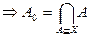 (перетинання кінцевого числа множин)
(перетинання кінцевого числа множин) 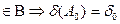 ;
;
2) припустимо, 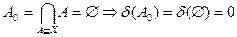 , з іншого боку
, з іншого боку 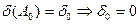 , прийшли до протиріччя, отже,
, прийшли до протиріччя, отже, 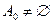 .
.
Теорема 4. (Кенига - Оре). У простому графі 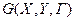 найбільше число дуг паросполучення дорівнює
найбільше число дуг паросполучення дорівнює 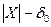 .
.
Доведення. Якщо 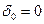 , то теорема зводиться до теореми Кенига - Холу. Допустимо,
, то теорема зводиться до теореми Кенига - Холу. Допустимо, 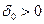 і розглянемо перетинання
і розглянемо перетинання 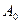 , перетинання тих множин
, перетинання тих множин 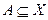 , для яких
, для яких 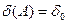 . По властивості 3,
. По властивості 3, 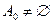 . Якщо видалити із графа
. Якщо видалити із графа 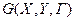 довільну вершину
довільну вершину 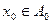 , то будуть зруйновані всі ті множини
, то будуть зруйновані всі ті множини  , для яких
, для яких 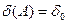 . Тому новий граф буде мати дефіцит
. Тому новий граф буде мати дефіцит 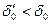 . Покажемо, що
. Покажемо, що 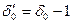 . Для множини
. Для множини 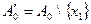 маємо
маємо 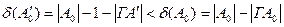 , тобто
, тобто 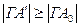 . Але в силу
. Але в силу 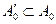 справедливо
справедливо 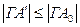 , отже,
, отже, 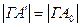 . Звідси
. Звідси 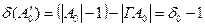 .
.
У силу нерівності 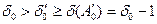 маємо
маємо  .
.
Видаляючи із множини 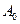 графа
графа 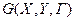
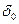 вершин, одержимо граф
вершин, одержимо граф 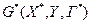 , дефіцит якого дорівнює 0. Він допускає паросполучення
, дефіцит якого дорівнює 0. Він допускає паросполучення 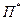 , що відображає множину
, що відображає множину 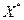 в множину
в множину 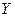 , тобто
, тобто 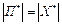
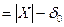 . Відповідно
. Відповідно 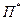 паросполучення
паросполучення 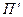 графа
графа 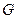 має те ж число дуг. Тому що, по теоремі 3
має те ж число дуг. Тому що, по теоремі 3 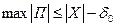 , то,
, то, 
 і теорема 4 доведена.
і теорема 4 доведена.
Опора. Опорою простого графа 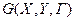 називається всяка така множина
називається всяка така множина 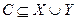 , що кожна дуга має принаймні одну зі своїх вершин в
, що кожна дуга має принаймні одну зі своїх вершин в 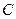 .
.
Визначення. Опора, що містить найменше число вершин, називається найменшою.
Якщо  - найменша опора і
- найменша опора і  є елемент опори, то
є елемент опори, то 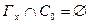 . Звідси слідує, що найменша опора представима у вигляді
. Звідси слідує, що найменша опора представима у вигляді  , де
, де 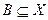 .
.
|
|
|
Теорема 5. (Кенига). У простому графі 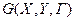 число вершин найменшої опори дорівнює числу дуг найбільшого паросполучення.
число вершин найменшої опори дорівнює числу дуг найбільшого паросполучення.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 330; Нарушение авторских прав?; Мы поможем в написании вашей работы!