
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
A) элементтері болса 7 страница
Отсюда получим искомое СДНФ
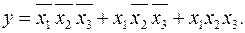
Второй способ преобразования функций общего вида в СДНФ (СКНФ) является аналитическим. Он связан с использованием следующих формул преобразования. 

1) 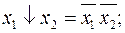 5)
5) 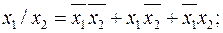
2) 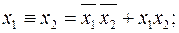 6)
6) 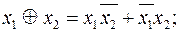
3) 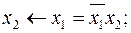 7)
7) 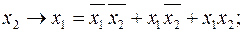
4) 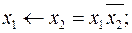 8)
8) 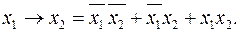

Эти формулы получены преобразованием табличной формы функций (таблица 1.4.1) в СДНФ. Аналогично представляются приведённые функции в СКНФ.
Пример 2.4.3. 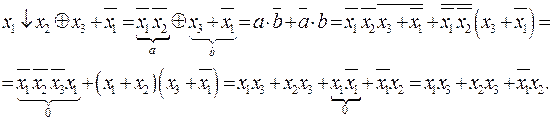


В общем случае логическая функция может иметь некоторое множество эквивалентных по логике, но разных по аналитическому представлению, вариантов. Эти варианты могут отличаться по составу независимых переменных и по числу логических операций, образующих функцию. В прикладном отношении возникает потребность поиска эквивалентного варианта представления функции с минимальным числом операций и, возможно, с меньшим числом независимых переменных. Процесс решения этого вопроса называется минимизацией логических функций.
При решении практических задач логического типа, их исходное аналитическое описание обычно представляется либо в СДНФ, либо в СКНФ. При всей своей структурной стройности эти формы, в большинстве своём, громоздки и нуждаются в минимизации.
Минимизация осуществляется путём направленного преобразования функции с помощью аксиом и законов алгебры логики. Для одной и той же функции может быть несколько путей достижения цели. Каждый такой путь обеспечивает нахождение минимальной формы функции сравнительно с исходной формой. Но, это ещё не означает, что цель достигнута. Тут надо знать следующее. В процессе преобразования могут быть достигнуты промежуточные и тупиковые формы функций. Тупиковая форма, в отличии от промежуточной, далее не минимизируется. Каждый возможный путь минимизации завершается тупиковой формой функции. У одной и той же функции тупиковых форм может быть несколько. Среди тупиковых всегда имеет место форма функции с меньшим числом логических операций (возможно и с меньшим числом независимых переменных). Её называют минимальной тупиковой формой функции. Существуют различные возможные исходы минимизации функций. Может быть несколько различных минимальных тупиковых форм. С точки зрения дальнейшего использования они почти всегда эквивалентны. В составе минимальных тупиковых форм могут присутствовать и не минимальные тупиковые формы. В простейшем случае функция имеет только одну минимальную тупиковую форму. Ну, и конечно, форма исходной функции может являться минимальной тупиковой. В этом случае говорят, что функция не минимизируется.
Существуют несколько методов минимизации логических функций. Рассмотрим некоторые из них.
2.5.1. Минимизация логических функций с использованием
аксиом и законов алгебры логики.
Данный метод можно назвать «ручным». В нём нет устоявшихся рекомендаций по рациональному поиску минимальных тупиковых форм функций. Успех минимизации зависит от уровня знания аксиом и законов алгебры логики и навыков их применения. Для сложных функций (число переменных 4 и более) этот метод предполагает многоходовые комбинации логических преобразований, которые приходится выполнять при минимизации. Такой процесс является довольно трудоёмким и не даёт никаких гарантий достижения требуемого минимума. Напротив, если функция проста, её минимизация осуществляется одно, двух, и, реже, трёхступенчатым преобразованием, не требующим особого труда и совершаемого почти автоматически. По этому данный метод целесообразно использовать для минимизации простых логических функций.
В процессе минимизации функций в той или иной мере используются все аксиомы и законы алгебры логики. Но, наиболее употребляемыми в этом случае, является:
- закон склеивания 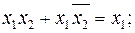 , (2.24)
, (2.24)
- закон поглощения  ;
;  , (2.25)
, (2.25)
- закон без имени 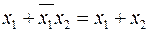 .
.
(2.26)
Пример 2.5.1.
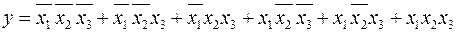 .
.
Склеим 1-ый и 4-ый, 2-ой и 5-ый, 3-ий и 6-ой минтермы
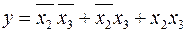 .
.
Продолжим минимизацию. Применим ко второму минтерму
аксиому 5 


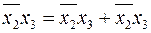
и подставим в полученный результат, тогда 
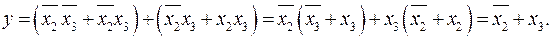

Это и есть искомый результат. Для его получения ещё раз использован закон склеивания.
Пример 2.5.2.

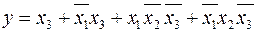 .
.
К 1-ому и 2-ому минтермам применим закон поглощения.

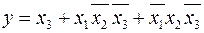 .
.
Так как 
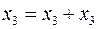 (аксиома 5),
(аксиома 5),

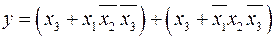 .
.
Для минимизации выражений в скобках используем закон без имени (2.26).

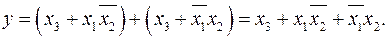
Пример 2.5.3.
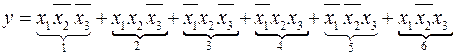 .
.
Первый вариант минимизации. Раздвоим 2-ый и 5-ий минтермы (аксиома 5). Полученную СДНФ скомпонуем следующим образом. 
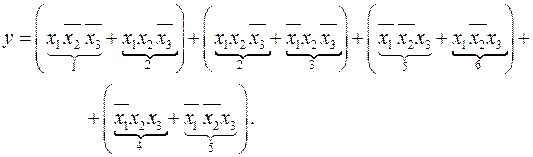 К выражениям в скобках применим закон склеивания. В результате получим первый вариант минимизации заданной функции.
К выражениям в скобках применим закон склеивания. В результате получим первый вариант минимизации заданной функции.

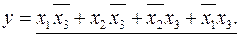
Второй вариант минимизации. Проведём иную компоновку минтермов заданной функции с последующим их склеиванием. 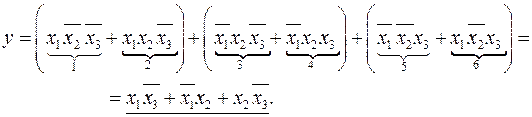

|
|
Дата добавления: 2014-11-09; Просмотров: 453; Нарушение авторских прав?; Мы поможем в написании вашей работы!