Свойства определителей

Способы вычисления определителей

Основные понятия и определения

Для квадратной матрицы А ее определитель обозначается 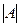или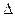

Определителем матрицы 1-го порядка А=(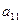) называется элемент .

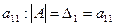Определителем 2-го порядка:

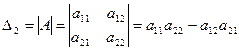
Например,

Пусть дана квадратная матрица 3-го порядка. Определитель 3-го порядка вычисляется по следующей схеме:

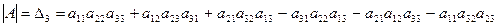
Другими словами, берутся следующие произведения:

со знаком «плюс» и

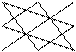
со знаком «минус».

Другой способ вычисления определителя 3-го порядка задается правилом Сарруса. Здесь к трем столбцам определителя дописываются первые два столбца, а в полученной конструкции произведения элементов берутся по диагоналям, наклон которых определяет знак того или иного произведения:

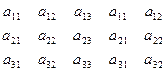со знаком”+”и

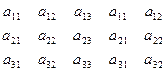со знаком “-“.

Пример: вычислим определитель

2 -1 -1

3 4 -2

3 -2 4

По правилу Сарруса

2 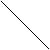-1 -1 2 -1

3 4 -2 3 4 =

3 -2 4 3 -2

2 -1 -1 2 -1

3 4 -2 3 4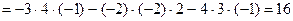

3 -2 4 3 -2

Отсюда значение определителя:

.

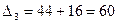Введем понятие определителя более высокого порядка. Рассмотрим квадратную матрицу n-го порядка:

…

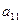
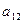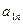
А= …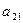

………………

…

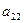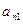
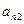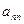
Общее число ее элементов равно 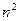. Из них выберем набор, содержащий n элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца.

Любой такой набор можно упорядочить, записав сначала элемент из 1-ой строки, затем из 2-ой и т.д.:

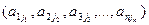(1)

Номера столбцов при этом 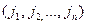образуют перестановку J из n чисел 1,2,…,n. Из комбинаторики известно, что существует всего n! Различных перестановок из n натуральных чисел.

Инверсия в перестановке J – это наличие пары чисел, в которой большее число предшествует меньшему.

Например, в перестановке J=(3,2.1) 3 инверсии:(3,2),(3,1),(2,1). Обозначим r(J) –количество инверсий в перестановке J. Каждому набору (1) можно поставить в соответствие произведение его элементов и число r(J).

Определителем квадратной матрицы n-го порядка называется число, равное следующей сумме:

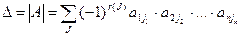(2)

где сумма берется по всем перестановкам J. Число слагаемых в этой сумме резко увеличивается с ростом n (оно равно n!), поэтому формула(2) неудобна для практических расчетов. При n=4 надо считать значения 24 произведений, при n=5- уже 120. Для вычисления определителей используют другие формулы.

Минором 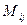элемента 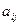квадратной матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием I-й строки и j-го столбца.

Например, минор элемента 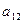матрицы 3-го порядка равен:

= =

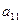
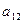
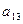
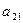
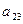
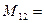
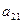
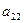
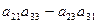
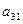
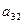
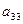
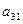
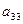
Каждая матрица n-го порядка имеет 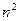миноров (n-1) –го порядка.

Алгебраическим дополнением 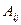элемента 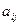квадратной матрицы n-го порядка называется его минор, взятый со знаком :

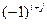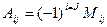
Пример: Найти алгебраические дополнения всех элементов матрицы

2 -1 1

2 1 1

А= 1 1 2.

2 1

1 1

Решение: 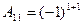1 2 =1; 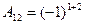1 2 = -3;

2 1

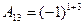1 1 =1 и т.д.

Теорема Лапласа. Определитель квадратной матрицы n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

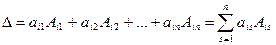
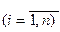(3)

(разложение по элементам I-строки);

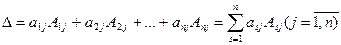(4)

(разложение по элементам j-го столбца)

Эта теорема сводит вычисление определителей n-го порядка к вычислению определителей (n-1)-го порядка.

Пример: Вычислим определитель матрицы:

5 3 0 7

0 -1 2 3

0 0 3 1

0 0 0 1

Решение: При использовании формул (3)-(4) удобнее выбрать строку или столбец с большим числом нулей; это дает экономию в вычислениях, поскольку алгебраические дополнения для нулевых элементов считать не нужно. Здесь разложим определитель по 1-му столбцу, где только один элемент не равен нулю:

-1 2 3 -1 2 3

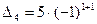0 3 1 =5 0 3 1

0 0 1 0 0 1

Далее вычислим определитель 3-го порядка. По аналогии разложим его по 1-му столбцу:

3 1

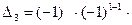0 1 =-3

Общий результат

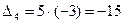
Свойства определителей

1. Если какая-либо строка (или столбец) матрицы состоит из одних нулей, то ее определитель равен нулю.

2. Если все элементы какой- либо строки (столбца) матрицы умножить на число 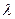, то ее определитель умножится на это число .

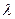Замечание. За знак определителя можно выносить общий множитель любой строки или столбца, в отличие от матрицы, за знак который можно выносить общий множитель лишь всех ее элементов.

3. При транспонировании матрицы ее определитель не изменяется: .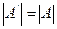

4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит 2 одинаковые строки(столбца), то ее определитель равен нулю.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю.

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю, т.е. 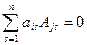при .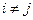

Замечание.: Свойство 7 и теорему Лапласа можно объединить:

.

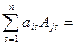
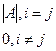
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и тоже число.

9. Сумма произведений произвольных чисел 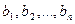на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .

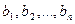10. Определитель произведения двух квадратных матриц равен произведению их определителей: 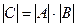, где С= 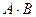, А и В – матрицы n-го порядка. Даже если АВ ВА, и в этом случае .

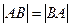Перечисленные свойства упрощают вычисления определителей.

Вопросы для самоконтроля:

1. Как вычислить определитель матрицы 2, 3, 4-го порядков?

Дата добавления: 2014-11-26