Понятие вектора

ВЕКТОРЫ

Вначале условимся о некоторых обозначениях. Точки будем обозначать прописными латинскими буквами: А, В, С, … Множество всех точек пространства (или просто пространство) обозначим символом Е³, произвольную прямую в пространстве – 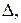произвольную плоскость – 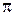. Если рассмотрение ограничивается только некоторой фиксированной плоскостью и нас не интересует ее расположение в пространстве, то данную плоскость будем обозначать символом Е². В аналогичной ситуации для прямой будем использовать обозначение Е¹.

В школьном курсе математики дается следующее определение вектора.

Определение 1.1.1. Вектором называется направленный отрезок прямой, т.е. отрезок, для которого одна из его граничных точек считается началом, а другая – концом.

Направленный отрезок будем обозначать символом 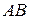; здесь 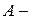начало, 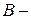конец. Случай, когда 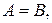не исключается, направленный отрезок 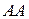называется нулевым. На письме (на доске, в тетради, в книге, на экране компьютера) направленный отрезок изображается в виде прямолинейной стрелки, направленной от начала к концу (рис. 1).

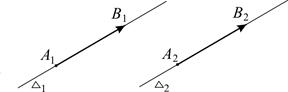
Рис. 1 Рис. 2

При недолгом размышлении над определением 1 возникает вопрос: почему для одного и того же объекта используются два названия – и направленный отрезок и вектор? Ответ кроется в последующем определении равенства векторов, принятом в школе. Оно показывает, что на самом деле, направленный отрезок и вектор – это два разных объекта. Действительно, рассмотрим две различные параллельные прямые 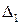и 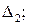выберем на них точк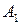и и 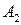соответственно и построим на этих прямых два направленных отрезка и 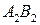, имеющих равные длины и одно и то же направление (рис. 2). Как направленные отрезки и 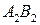, очевидно, различны, а как векторы – равны. Возникшая ситуация объясняется тем, что термин "равенство" в школе используется в различных смыслах (сравните, например, школьные определения равенства векторов и равенства треугольников). Мы постараемся избегать неоднозначного толкования одного и того же слова и будем понимать под термином "равенство" тождественное совпадение. Таким образом, два объекта равны, если это один и тот же объект (обозначенный, возможно, различным образом). Это означает, например, что есл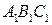и и 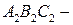треугольники, то они равны, если совпадают как множества точек[4].

Итак, уточняя школьное определение вектора, мы оставляем за направленным отрезком его название, а вектор определим иначе.

Если есть два ненулевых направленных отрезка, которые лежат на параллельных прямых или на одной прямой, то выполняется одно из двух условий: либо они одинаково направлены (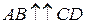), либо противоположно направлены (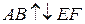) (рис. 3).

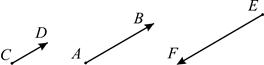
Рис. 3

Будем считать, что мы всегда можем отличить первую ситуацию от второй[5]. Ненулевые отрезки, лежащие на непараллельных прямых, не являются одинаково или противоположно направленными.

Определение 1.1.2. Направленный отрезок 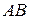называется эквивалентным направленному отрезку 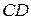(обозначение 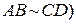, если длина отрезка 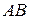равна длине отрезка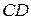 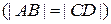и отрезк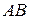и и 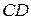одинаково направлены (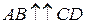). Все нулевые отрезки эквивалентны между собой 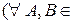Е³ и никакой нулевой отрезок не эквивалентен никакому ненулевому.

Утверждение 1.1.1. Пусть 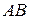и 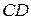– направленные отрезки. Тогда следующие утверждения равносильны:

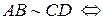середина отрезка совпадает с серединой отрезка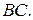

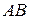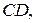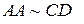Доказательство. Необходимость. Пусть вначале хотя бы один из отрезков, или нулевой, например, Тогда условие означает, что следовательно, отрезки и 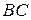совпадают, а значит, совпадают и их середины (рис. 4).

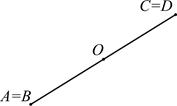
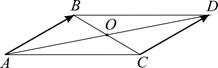
Рис. 4 Рис. 5

Пусть теперь оба отрезка 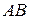и 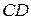ненулевые и не лежат на одной прямой. Тогда четырехугольник 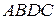параллелограмм, и 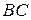его диагонали, которые, как известно, пересекаются и в точке пересечения делятся пополам (рис. 5).

Пусть, наконец, отрезки 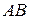и 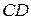ненулевые и лежат на одной прямой Тогда в зависимости от взаимного расположения точек 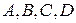на прямой возможны 3 различных случая. Если отрезк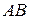и и 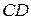не пересекаются, то множество 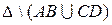является объединением двух лучей и открытого интервала, расположенного между отрезкам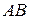и и 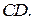В этом случае точка О совпадает с серединой упомянутого интервала (рис. 6, а). Если отрезк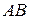и и 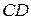пересекаются в одной точке, то эта точка совпадает с точкой О (рис. 6, б).Еслипересечение отрезков 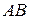и 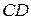содержит более одной точки, то это пересечение есть отрезок, середина которого совпадает с точкой О (рис. 6, в).

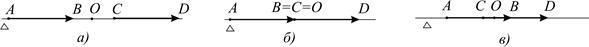
Рис. 6

Достаточность. Если отрезки и 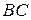не лежат на одной прямой, то четырехугольник 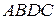параллелограмм, поскольку его диагонали в точке пересечения делятся пополам. Следовательно, 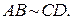Если же отрезки и 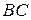лежат на одной прямой, то, как и в случае необходимости, следует рассмотреть несколько различных случаев взаимного расположения точек 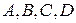. В каждом из них эквивалентность направленных отрезков 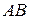и 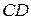легко устанавливается. 

Следствие 1.1.1. Длялюбых точек 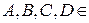Е³ верны эквивалентности:

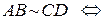
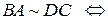
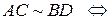
Доказательство. Действительно, в силу утверждения 1.1.1, эквивалентность каждой из четырех пар направленных отрезков равносильна одному условию: середины отрезков и 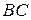совпадают.

Из определения 1.1.2 очевидно вытекают следующие свойства отношения эквивалентности направленных отрезков.

(i) 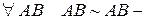свойство рефлексивности;

(ii) если 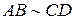, то свойство симметричности;

(iii) если 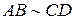и то 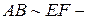свойство транзитивности.

Свойства (i) – (iii) означают, что отношение эквивалентности направленных отрезков является отношением эквивалентности (в смысле теории множеств[6]) в множестве всех направленных отрезков пространства. Тем самым, множество всех направленных отрезков пространства Е³ разбивается на классы эквивалентности.

Определение 1.1.3. Вектором называется класс эквивалентных направленных отрезков.

Векторы будут обозначаться строчными латинскими буквами со стрелкой наверху: 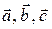, … Таким образом, каждый вектор 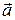представляет собой бесконечное множество направленных отрезков, эквивалентных между собой: 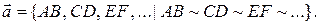Изобразить вектор, т.е. все направленные отрезки, составляющие данный вектор, невозможно, обычно рисуют один из них и ставят обозначение вектора (рис. 7,8, 9, …).

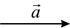
Рис. 7

Каждый направленный отрезок, составляющий данный вектор, называется представителем этого вектора. Если 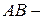представитель вектора 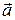, то для вектора 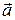используют также обозначение 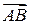. По определению, все нулевые отрезки образуют один класс эквивалентности. Этот вектор называется нулевым и обозначается 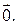Множество всех векторов пространства обозначим V (E³).

Имея дело с векторами, часто используют термин система векторов. В отличие от понятия множества векторов, которое означает набор попарно различных векторов,под системой векторов понимается произвольный набор векторов 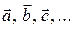, конечный либо бесконечный, в котором некоторые векторы могут повторяться.

Пусть 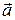– ненулевой вектор. Поскольку все направленные отрезки, составляющие вектор 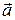, имеют одну и ту же длину и одно и то же направление[7], то эта длина и это направление называются длиной и направлением вектора 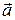. Длина вектора 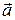обозначается 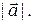Очевидно, что длиной и направлением вектор определяется однозначно. Длина нулевого вектора равна нулю, а его направление не определено. Для удобства считают, что нулевой вектор одинаково направлен с каждым вектором.

Пусть даны точка 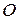и вектор 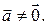Через точку 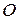можно провести единственную прямую, одно из направлений которой совпадает с направлением вектора 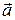, и единственным образом в этом направлении отложить отрезок 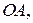длина которого равна длине вектора 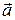. Эта операция построения по точке 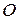и вектору 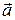точки 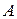такой, что направленный отрезок 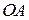представляет вектор 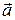, т.е. 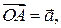называется откладыванием вектора от точки. Понятно, что нулевой вектор от точки 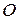также откладывается однозначно, при этом получается точка 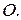Таким образом, откладывание вектора от точки – это отображение

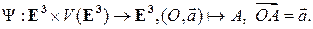
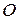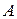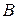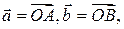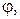
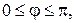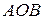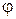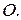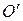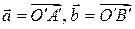Пусть – ненулевые векторы. Отложив их от некоторой точки , т.е. построив точки и такие, что можно говорить о числе измеряющим (в радианах) величину угла (рис.8). Отметим, что число не зависит от выбора точки Действительно, если отложить векторы от другой точки (), то углы 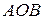и 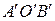имеют попарно параллельные и одинаково направленные стороны, поэтому их величины равны. 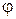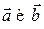Число называется величиной угла между векторами Векторы называются ортогональными (перпендикулярными), если величина угла между ними равна 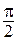(обозначение: 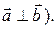Нулевой вектор считается ортогональным любому вектору.

Определение 1.1.4. Пусть 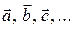– некоторая система векторов. Векторы 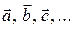называются коллинеарными (компланарными), если при откладывании их от некоторой точки 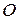получающиеся точки 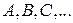лежат на одной прямой 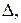проходящей через точку 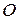(рис. 9) (в одной плоскости 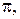проходящей через точку 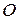). В случае коллинеарности или компланарности говорят также, что векторы 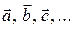параллельны прямой 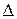( 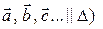или плоскости (

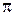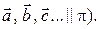
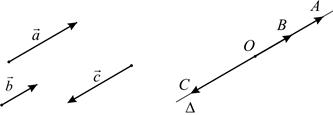
Рис. 8 Рис. 9

Для того, чтобы определение 1.1.4 было корректным нужно, как и при определении величины угла между векторами, убедиться, что оно не зависит от выбора точки 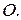Простые рассуждения, доказывающие этот факт, предлагается провести читателю в качестве упражнения.

Точно так же, как в случае пространства, можно определить понятие вектора плоскости Е² (или прямой Е¹ ) как класса эквивалентных направленных отрезков этой плоскости (прямой). Множество всех векторов плоскости обозначим V (E²), множество всех векторов прямой – V (E¹).

Пусть теперь 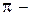плоскость, рассматриваемая как подмножество пространства ( 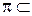E³). Формально множество векторов плоскости V (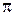) не является подмножеством множества V (E³) всех векторов пространства, поскольку никакой вектор плоскости не является вектором пространства. Действительно, любой вектор 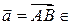V (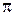) есть множество всех направленных отрезков плоскости 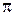, эквивалентных направленному отрезку

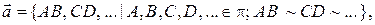
в то время как вектор 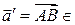V (E³) пространства есть множество всех эквивалентных направленных отрезков пространства, эквивалентных отрезку

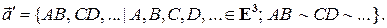
Ясно, что множество 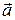(класс направленных отрезков) является собственным подмножеством множества 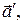т.е. 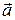не совпадает с 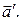Тем не менее, множество V (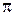) можно естественным образом вложить в множество V (E³), поставив в соответствие каждому вектору 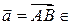V (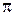) вектор 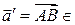V (E³). Отображение вложения

V (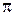) 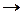V (E³), 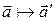(1)

заключается в расширении множества 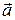до множества 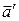путем добавления к 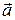недостающих направленных отрезков пространства, эквивалентных отрезку 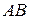. Очевидно, что отображение (1) инъективно, т.е. действительно является вложением. Примем следующее соглашение.

Для любой плоскости 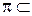E³ будем отождествлять вектор 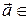V (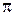) с его образом 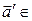V (E³) при вложении (1) и считать, что V (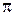) 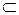V (E³).

Если 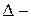некоторая прямая, 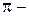плоскость, и 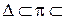E³, то рассуждения, аналогичные вышеприведенным, позволяют считать, что 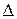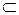V () V (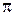) 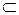V (E³).

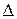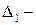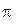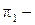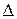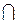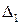Упражнение 1.1.1. Пусть и прямые, и плоскости в пространстве E³. Найдите пересечения V (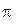) 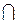V (), V (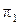) V (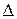)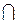, V () V ().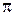

Дата добавления: 2014-11-09