Основные понятия, величины, модели, законы статистической физики

В статистической физике изучают состояния и процессы, происходящие с системами, состоящими из очень большого числа частиц классических либо квантовых. Такие системы называют макросистемами. В макросистеме различают подсистемы, содержащие также большое число частиц. Состояние системы описывается макроскопическими (макропараметрами) и микроскопическими параметрами (микропараметрами). Макропараметры - физические величины, характеризующие систему в целом, например, температура, давление. Микропараметры - физические величины, характеризующие каждую частицу в отдельности, например, скорость, энергия частиц. Макропараметры связаны с микропараметрами по определенным правилам. Задание макропараметров обеспечивает знание макросостояния системы.

Для описания микросостояния системы используется набор микропараметров, которые не одинаковы для классических и квантовых частиц. Если система состоит из 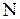классических частиц, то состояние каждой частицы характеризуется тремя координатами и тремя проекциями импульса. Следовательно, микросостояние системы 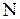классических частиц характеризуется 6N микропараметрами. Совокупность 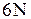микропараметров образует условное 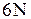- мерное фазовое пространство. Каждому микросостоянию системы в фазовом пространстве соответствует точка, а изменение состояния характеризуется фазовой траекторией. Макросостояние системы 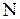квантовых частиц описывается квантовыми числами, а соответствующее фазовое пространство является - мерным. Каждому микросостоянию системы в фазовом пространстве соответствует не точка, а фазовая ячейка определенного минимального объема.

Все общефизические законы справедливы и для описываемых статистической физикой состояний и процессов. В статистической физике используются инерциальные системы отсчета; и рассматриваются чаще всего скорости движения частиц систем и скорости протекания процессов значительно меньшие скорости света; системы частиц считаются неподвижными относительно выбранной инерциальной системы отсчета, поэтому законы сохранения импульса и момента импульса системы не находят практического применения, что же касается закона сохранения энергии, то он имеет важное значение и в статистической физике. Фундаментальная и принципиально новая по сравнения с механикой идея статистической физики состоит в признании случайного вероятного значения микропараметров для частиц в системе. Случайный характер параметров состояния учтен вероятностью нахождения точки в элементе объема фазового пространства, т.е. вероятностью иметь частице те или иные параметры движения.

Понятие вероятности не сводится к более простым и поэтому постулируется. Вероятность характеризует долю случайных событий с данным исходом от общего числа событий, происшедших в одних и тех же условиях. Пусть в некоторой макросистеме, находящейся в определенном состоянии, измеряется в одинаковых условиях 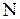раз микропараметр х и получены значения: 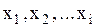, причем 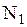измерений дали значения 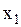, 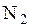измерений дали 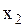, 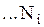измерений дали , так что 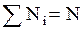. (3.1.1)

Тогда 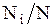есть относительная частота появления результата , а

(3.1.2)

- есть вероятность появления результата . Из (3.1.1) и (3.1.2) следует:

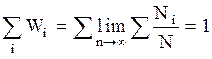, (3.1.3)

т.е. сумма вероятностей всех возможных результатов измерения равна единице. Через вероятности различных результатов измерения можно выразить среднее значение измеряемой величины. Из определения среднего значения и (3.1.2)

получим 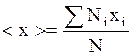. (3.1.4)

Рассмотрим случай, когда измеряемая величина принимает непрерывный ряд значений от 0 до ¥. Пусть, например, сделано 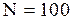измерений координаты частицы в одинаковых условиях или, что то же самое, одновременно измерены координаты ста частиц одной системы, называемой также статистическим ансамблем. По результатам измерений оказалось, что 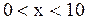см. Выберем малый интервал, например, в 1 см и найдем, сколько частиц имеют координаты в интервалах от 0 до 1 см, от 1 см до 2 см,...... от 9 до 10 см. Полученные данные приведены в таблице 3.1. Построим по этим данным столбчатую диаграмму (гистограмму) (рис. 3.1), которая характеризует вероятность получения результатов измерений, заключающихся в различных интервалах шириной каждый 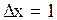см.

Таблица 3.1

Интервалы координат Dх, см	Относительная частота, DNi / N
0... 1	0.02
1... 2	0.06
2... 3	0.20
3... 4	0.37
4... 5	0.22
5... 6	0.10
6... 7	0.06
7... 8	0.04
8... 9	0.02
9... 10	0.01

Чем меньше выбрать ширину интервала 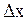, тем точнее будет охарактеризовано распределение вероятностей значений координат частиц. В пределе 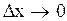ступенчатая линия, ограничивающая гистограмму превратится в гладкую кривую (рис. 3.2).

Функция 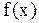, определяющая эту кривую аналитически, называется функци-

ей распределения вероятности или плотностью вероятности. В рассмотренном примере обсуждалось распределение частиц по координатам. Из рис. 3.2. площадь столбика шириной равна

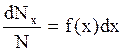, (3.1.5)

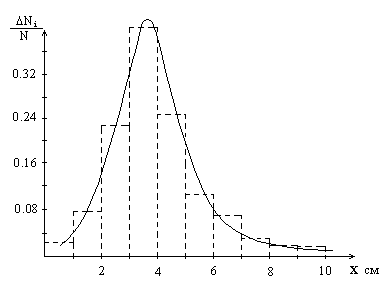
Рис. 3.1

Рис. 3.2

а по смыслу это есть вероятность 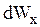того, что результат измерения координаты окажется в интервале от 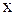до . Следовательно,

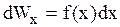. (3.1.6)

Площадь по кривой распределения 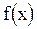, как и площадь гистограммы, равна единице, как суммарная вероятность всех результатов измерений, т.е.

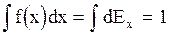. (3.1.7)

Если в каком либо случае выполняется (3.1.7), то говорят, что функция распределения 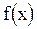нормирована на единицу, а (3.1.7) является условием нормировки 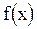. Интегрирование В (3.1.6) производится по всему интервалу возможных значений 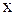. Зная функцию распределения 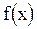можно найти среднее значение измеряемой величины 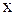. Из определения среднего значения (3.1.5) и (3.1.6) получим

. (3.1.8)

Если 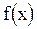не зависит явно от времени, то система находится в состоянии статистического равновесия или, в равновесном состоянии, которое чаще всего исследуется в статистической физике. Всякая система стремится перейти в равновесное состояние, из которого самопроизвольно не выходит. Поэтому вероятность равновесного состояния считают наибольшей. Для получения функции распределения нужно учесть законы движения и взаимодействия частиц в системе. Следовательно, вид функции распределения для различных систем частиц различны и является одним из основных законов в статистической физике для данной системы частиц. С некоторыми функциями распределения познакомимся позже. В равновесном состоянии средние значения макропараметров системы не изменяются со временем, а потому имеют одинаковые значения для всей системы. Однако конкретные значения физических величин не совпадают со средними, а отклоняются от них. Случайные отклонения от среднего значения называют флуктуациями. В равновесном состоянии флуктуации очень малы, поэтому макропараметры с высокой точностью описывают состояния макросистемы. Наличие флуктуаций и является выражением статистического вероятностного характера состояния системы из большого числа частиц.

Одним из основных законов статистической физики является эргодическая гипотеза, т.е. подтверждение о том, все микросостояния системы одинаковы вероятны. Всякое макросостояние системы может быть осуществлено большим числом различных микросостояний. Число различных микросостояний соответствующих данному микросостоянию называется статистическим весом макросостояния и обозначается (омега).

Исходя из эргодической гипотезы и определения статистического вела макросостояния можно утверждать, что вероятность макросостояния пропорциональна статистическому весу этого состояния. Когда равновесное состояние системы, как наиболее вероятное состояние, обладает максимальным статистическим весом.

Дата добавления: 2014-11-16