Лекция № 64. Тема 6 : Основные законы распределения случайных величин

6.1. Дискретные законы распределения

6.1.1. Биномиальное распределение

Определение 1. Биномиальным называется распределение вероятностей, определяемое формулой Бернулли в виде таблицы

X			…	k	…	п
p			…		…

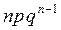
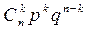
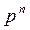
где Х - количество появлений события А в п повторных испытаниях, если вероятность его появления в каждом из испытаний не изменяется и равно р. Пусть - число появления события A в i -ом испытании, т.е.

p	q	p

тогда и

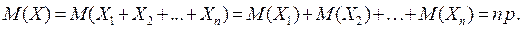
Аналогично можно показать, что .

Пример 1. ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно равна 0,9. В каждой партии 5 изделий. Найти , где X - число партий, в каждой из которых окажется ровно 4 стандартных изделия, если проверки подлежат 50 партий.

Вначале определим вероятность того, что в каждой партии окажется ровно 4 стандартных изделия

Тогда

6.1.2. Распределение Пуассона

Пусть в схеме Бернулли производится n опытов, в которых вероятность появления события А мала, а n велико и .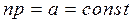

Определение 2. СВ X распределена по закону Пуассона, если вероят-ность того, что она примет определённое значение k, выражается формулой

Пуассона 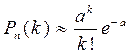, т.е. закон распределения имеет вид

X			…	k	…
p			…		…

Тогда .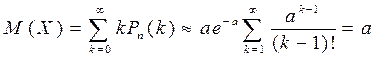

Аналогично можно показать, что .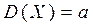

Пример 2. Автозавод отгрузил 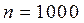автомобилей. Вероятность повреждения автомобиля при транспортировке . Определить веро-ятность того, что автомагазин получит 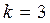повреждённых автомобилей.

Вначале определим математическое ожидание .

Тогда

6.1.3. Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р, а, значит, вероятность непоявления события А равна . Испытания заканчиваются в момент появления события А. Следовательно, если событие А появи-лось в k -ом испытании, то в предыдущих k - 1 испытаниях оно не появля-

лось, т.е. описываемое событие имеет вид .

Отсюда получим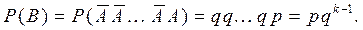

Обозначим через Х дискретную случайную величину – число испы-таний, которые необходимо провести до появления события А. Таким образом СВ Х может принимать только значения 1, 2, 3, …

Определение 3. СВ X распределена по геометрическому закону, если вероятность того, что она примет определённое значение k, выражается формулой 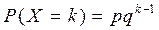, т.е. закон распределения имеет вид

X				…	k	…
p	p			…		…

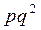
Нетрудно убедиться, что сумма всех вероятностей, как сумма членов бесконечно убывающей геометрической прогрессии, равна

Тогда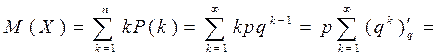

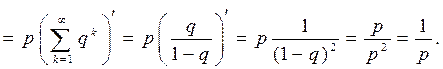
Аналогично можно показать, что .

Пример 3. Студент может сдать экзамен по высшей математике с вероятностью 0,6. Определить вероятность того, что:

а) студент сдаст экзамен с третьей попытки;

б) студент сдаст экзамен за три попытки.

Имеем 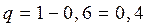и вероятность того, что студент сдаст экзамен с третьей попытки

Вероятность того, что студент сдаст экзамен за три попытки

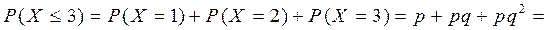
6.2. Непрерывные законы распределения

6.2.1. Равномерное распределение

В некоторых задачах практики встречаются непрерывные СВ, о которых известно, что их возможные значения находятся в некотором промежутке, где они одинаково вероятны. О таких СВ говорят, что они распределены по закону равномерной плотности. Из такого понятия следует, что их функция плотности распределения имеет вид

Определим константу С из свойства 4 функции плотности

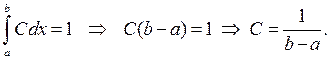
Легко найти интегральную функцию распределения

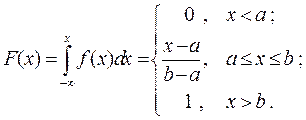
и основные числовые характеристики равномерного распределения:

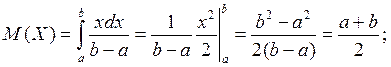
Пример 1. Колесо приводится во вращение, а затем останавливается под действием сил трения. Угол - случайная величина, равномерно распре-делённая в промежутке 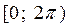. Найти её числовые характеристики.

6.2.2. Показательное распределение

Определение 3. Показательным (экспоненциальным) распределением называется распределение, которое имеет функцию плотности вида

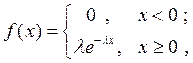
с параметром .

Найдём интегральную функцию этого распределения

Приведём графики дифференциальной и интегральной функций пока-зательного распределения.

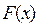
1

0 х 0 х

Найдем основные числовые характеристики показательного распреде-ления – математическое ожидание:

Аналогично, используя формулу интегрирования по частям дважды, находим и дисперсию

т.е. для показательного распределения выполняется соотношение

Показательное распределение широко используется в теории надёжности. Пусть элемент некоторого устройства начинает работать в момент времени , а в момент t происходит отказ в работе. Обоз-начим через T непрерывную СВ – время безотказной работы элемента, а через - интенсивность отказа (среднее число отказов в единицу времени), тогда функция распределения

определяет вероятность отказа элемента за время t, а функция

вероятность безотказной работы за 1

время t. Она называется функцией

надёжности. Ее график подобен

графику функции плотности

показательного распределения 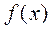. t

Пример 2. СВ Т - время безотказной работы станка имеет показательное распределение. Определить вероятность того, что время безотказной работы станка будет не менее 6000 часов, если среднее время безотказной работы станка 4000 часов.

Здесь математическое ожидание и тогда

Характеристическое свойство показательного закона надежности:

Вероятность безотказной работы устройства на интервале времени длительности t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от времени t.

Действительно, обозначим события:

А – безотказная работа устройства на интервале времени ;

В – безотказная работа устройства на интервале времени ;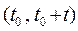

А В – безотказная работа устройства на интервале времени .

Найдем вероятности этих событий

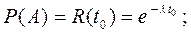
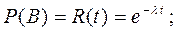
Найдем условную вероятность того, что устройство будет работать безотказно на интервале времени 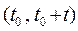при условии, что оно уже проработало безотказно на предыдущем интервале времени

Как видим, полученная формула не содержит , а содержит только величину времени t.

Другими словами, в случае показательного закона надежности прошлая работа устройства не влияет на вероятность его будущей безотказной работы, что очень удобно для решения практических задач.

Дата добавления: 2014-11-16