Правила записи точечных групп симметрии

Понятие о точечной группе (классе) симметрии

Точечные группы (классы) симметрии кристаллов

Пусть имеется множество G однотипных (т. е. имеющих общие характерные признаки) элементов

G ={ g ₁, g ₂,..., g_k,... }. (5.1)

Элементами множества G могут быть различные математические объекты: числа, матрицы, преобразования пространства, операторы и т.д.

Для каждой упорядоченной пары из этого множества ставится в соответствие по некоторому правилу единственный элемент из этого же множества G. Операция называется «умножением» и обозначается знаком «*». Смысл термина «умножение» должен быть объяснен в каждом конкретном случае и может не иметь ничего общего с обычным умножением.

Так, если элементы g_i и g_k принадлежат множеству G (), то и поставленный им в соответствие элемент g_m также принадлежит множеству G, т. е.

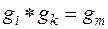, (5.2)

При этом обычно говорят, что множество G замкнуто относительно заданной операции умножения.

Рассмотрим пример определения операции «умножения» для вращения правильного треугольника против часовой стрелки вокруг оси, проходящей через его центр О (рис.5.1).

Рис. 5.1. К определению операции «умножения» при вращении правильного треугольника

Будем считать два поворота совпадающими, если они отличаются друг от друга на целое число полных оборотов (т.е. на целочисленное кратное 360^о), так как поворот на целочисленное кратное 360^о ставит каждую вершину на ее первоначальное место (нулевой поворот). Очевидно, что из всех возможных поворотов треугольника лишь три поворота переводят треугольник в себя, а именно: повороты на 120^о, 240^о и нулевой поворот. Первый поворот переводит вершину А в вершину В, вершину В в вершину С, вершину С в вершину А (перемещает вершины в циклическом порядке А, В, С). Второй поворот перемещает А в С, В в А, С в В (перемешает в циклическом порядке А, С, В).

Теперь введем определение для умножения операций поворота. Умножить два поворота – это значит последовательно произвести их один за другим. Таким образом, поворот на 120^о, умноженный с самим собой, дает поворот на 240^о, умноженный с поворотом на 240^о дает поворот на 360^о, т.е. нулевой поворот. Два поворота на 240^о дают поворот на 480^о = 360^о + 120^о, т.е. их произведение есть поворот на 120^о.

Если нулевой поворот обозначить а_о, поворот на 120^о через а₁, поворот на 240^о через а₂, то получим следующие соотношения:

, ,

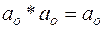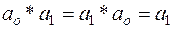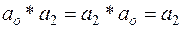, , (5.3)

, .

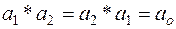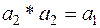Множество G называется группой, если для его элементов умножения выполняются следующие условия:

1. Умножение ассоциативно, т. е.

. (5.4)

2. Среди элементов g_i множества G есть элемент 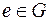такой, что

. (5.5)

Элемент е называется единичным (тождественным, нейтральным) элементом группы G.

3. Для каждого элемента g_i можно найти элемент, обозначаемый обычно через , принадлежащий тому же множеству G, такой, что

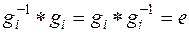. (5.6)

Элемент называется элементом, обратным элементу g_i.

Перечисленные свойства множества G, определяющие его как группу, называются групповыми аксиомами.

Покажем, что совокупность всех симметрических преобразований любой пространственной фигуры образует группу в математическом смысле. Для того чтобы множество операций симметрии образовывало группу, должны выполняться следующие законы:

1. Произведение двух симметрических преобразований пространственной фигуры является симметричным преобразованием той же фигуры.

2. Справедлив сочетательный закон — в тройном произведении симметрические преобразования можно менять местами.

3. Существует единичное симметрическое преобразование, такое, что произведение его на любое симметрическое преобразование данной пространственной фигуры равно этому симметрическому преобразованию.

4. Для каждого симметрического преобразования пространственной фигуры существует обратное симметрическое преобразование, такое, что их произведение равно единичному преобразованию.

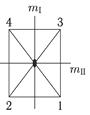
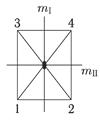
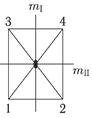
Возьмем для простоты пространственную геометрическую фигуру — прямоугольную пирамиду (рис. 5.2) и проверим на ней, подчиняются ли ее симметрические преобразования групповым законам.

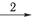
Рис. 5.2. Симметрические преобразования группы mm2, иллюстрирующие выполнение групповых законов (прямоугольная пирамида, спроецированная на плоскость рисунка)

Симметрия этой фигуры характеризуется следующими преобразованиями: отождествлением, поворотом на 180° и двумя отражениями в плоскостях m _I и m _II. Для удобства пронумеруем углы пирамиды, как показано выше.

Проверим первый признак группы и произведем последовательно две операции: поворот на 180° и отражение в плоскости m _I. Произведение этих двух операций эквивалентно отражению в плоскости m _II, а это симметрическое преобразование принадлежит к той же группе.

Одним из способов описания конечной группы является ее представление в виде таблицы умножения (таблица или квадрат Кейли). Чтобы получить квадрат Кейли для группы, строят квадратную таблицу, в первой строке и первом столбце которой записываются все элементы группового множества. На пересечении каждой строки и столбца записывается элемент группы, являющийся результатом умножения соответствующих элементов, находящихся в первой строке и первом столбце. Для вышеприведенной группы mm 2 таблица Кейли (5.7) выглядит следующим образом:

	е		m I	m II
е	е		m I	m II
		е	m II	m I
m I	m I	m II	е
m II	m II	m I		е

    (5.7)

Таблица Кейли обладает рядом важных свойств:

1. Ни в одной строке (или столбце) не содержится повторяющихся элементов.

2. Любая из строк является некоторой перестановкой верхней строки.

3. Нейтральный элемент расположен симметрично относительно главной диагонали.

Легко проверить и другие законы группового действия. За единичный элемент группы симметрических преобразований можно выбрать любой из них, а за обратный элемент — любое симметрическое преобразование в обратном направлении.

Итак, симметрические преобразования пространственных фигур образуют группы. Эти группы называют точечными - группами симметрии, потому что при всех преобразованиях остается неподвижной одна точка в начале координат.

Число различных операций симметрии (количество элементов группы), входящих в группу, называется порядком группы. Например, для группы 6 число операции симметрии равно 6: 1, 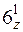, , , , 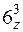или в условных обозначениях 6{1, 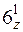, , , , 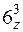}; для группы 2/ m – 4: 1, 2_z, m _z, или 2/ m {1, 2_z, m _z, } и т.д. Группа называется конечной, если число ее элементов конечно.

Структура группы определяется заданием результата «умножения» каждой упорядоченной пары элементов либо путем перечисления, либо же путем указания функционального закона, без какой бы то ни было конкретизации природы элементов.

В общем случае элементы группы могут не коммутировать, например, , поэтому порядок записи произведения должен быть четко определен. Из аксиом группы видно, что единичный элемент 1 коммутирует со всеми элементами группы.

В том случае, когда элементы группы коммутируют, группа называется абелевой; в этом случае таблица Кейли должна быть симметричной относительно главной диагонали. Например, группы mm 2, 222, 2/ m являются абелевыми:

mm 2	1	mx	my	2z
1	1	mx	my	2z
mx	mx	1	2z	my
my	my	2z	1	mx
2z	2z	my	mx	1

	1	2x	2y	2z
1	1	2x	2y	2z
2x	2x	1	2z	2y
2y	2y	2z	1	2x
2z	2z	2y	2x	1

2/ m	1	2y	my
1	1	2y	my
2y	2y	1		my
my	my		1	2y
		my	2y	1

Если все элементы группы могут быть получены как степени единственного элемента (например, для группы 6: , , , , ), то такая группа называется циклической.

Элемент группы или несколько элементов (если группа не циклическая), при помощи которых можно путем умножения получить все элементы группы, называются производящими элементами или генераторами.

Когда порядок группы велик, задание ее свойств при помощи таблицы Кейли оказывается слишком громоздким, и в этом случае более целесообразно описывать структуру при помощи множества производящих элементов (генераторов) и множества определяющих соотношений, которые показывают, как получить нейтральный элемент из генераторов и их произведений. Например, для группы 222 генераторами являются 2_z, 2_x; для группы mmm – 2_z, 2_x, .

В некоторых случаях, часть операций, входящих в группу, сама по себе составляет группу (меньшего порядка, чем исходная). Эта группа по отношению к исходной называется подгруппой, исходная по отношению к ней – надгруппой. Так у группы 2/ m три подгруппы: 2{1, 2_y }, m {1, m_y } и { , 1}; у группы 32 – четыре: 3{1, 3_z, 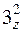}, 2{1, 2_x }, 2{1, 2_y }, 2{1, 2_z }.

Тот факт, что группа - подгруппа группы 2/ m, обозначается 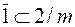. Группа 1, состоящая из единственной операции 1, - подгруппа любой группы, поэтому ее часто называют тривиальной подгруппой и опускают при перечислении подгрупп.

Отношение порядка группы к порядку подгруппы называется индексом подгруппы; так по отношению к группе 32 группа 3 оказывается подгруппой индекса 2, а группа 2 – подгруппой индекса 3; по отношению к группе 2/ m группы 2, m и - подгруппы индекса 2.

Точечные группы, кроме свойств, перечисленных в аксиомах, могут иметь многие другие свойства: могут быть центросимметричными и ацентричными, голоэдрическими и мероэдрическими и т.д.

Кристаллографически различные точечные группы могут быть абстрактно одинаковыми, т.е. иметь одинаковые таблицы умножения. Такие точечные группы называются изоморфными. Всем кристаллографически различным, но изоморфным между собой группам соответствует одна и та же абстрактная группа; например, коммутативные группы 2/ m, 222 и mm 2.

Для обозначения кристаллографических классов (точечных групп) симметрии применяются символы, основанные на теоремах об умножении операций симметрии. Существуют несколько систем обозначений точечных групп: международная система (Германа-Могена), Шенфлиса, Бравэ.

В международной системе обозначений Германа-Могена сначала записывают число, обозначающее порядок главной оси симметрии n (1, 2, 3, 4, 6), затем пишут символы т или 2 столько раз, сколько плоскостей или осей 2 существует наряду с главной осью симметрии. Если плоскость симметрии перпендикулярна главной оси, то перед ее символом т ставят косую черту, если она параллельна, то черту не ставят, или записывают в виде дроби. Символом 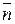обозначают инверсионно-поворотную ось.

Например, запись nm обозначает группу с одной осью n -го порядка и n плоскостей симметрии, прохо­дящих вдоль нее; 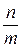или п/т – группу, которой отвечаетось симметрии n -гoпорядка и перпендикулярная ей плоскость симметрии; п2 - группу с осью симметрии п- гопорядка и п осями 2-го порядка, ей перпендикулярных; или п/тт — группу с осью симметрии n -го порядка и плоскостями т, параллельными и перпендикулярными ей (п и 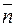могут иметь значения 1, 2, 3, 4, 6).

В системе Германа-Могена обозначений элементов симметрии указывается минимальное число элементов, достаточное для определения точечной группы симметрии – пишутся только порождающие элементы симметрии – плоскости или оси. Максимальное число позиций в обозначении группы – 3, каждая из них занята неэквивалентными особыми элементами.

При записи или чтении международ­ного символа необходимо соб­людать правила кристаллографичес­кой установки и порядок записи: смысл цифры или буквы, обозначающей элемент симметрии, зависит от того, на какой позиции в символе она постав­лена. Правила записи международных символов точечных групп и правила кристаллографической установки све­дены в табл. 5.1.

В международной символике разли­чают «координатные» элементы сим­метрии, проходящие вдоль коорди­натных плоскостей, и «диагональ­ные» - по биссектрисам углов между ними.

В низшей категории элементы симметрии расположены следующим образом: особое направление по оси X – на 1-м месте, особое направление по оси Y – на 2-м месте, особое направление по оси Z – на 3-м месте (табл.5.1).

Таблица 5.1

Дата добавления: 2014-11-16