Тема 9.Дифференциальные уравнения

Основные теоретические сведения.

1. Общим решением дифференциального уравненияпервого порядка называется дифференцируемая функция y = 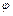(х, С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y = 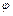(х, С) при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям y= 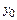при 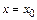(другая запись 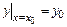), называется задачей Коши.

График всякого решения y = 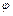(х) данного дифференциального уравнения, построенный на плоскости хОy, называется интегральной кривой этого уравнения.

2. Уравнение вида у ′+ А (х) у = В (х) называется линейным. Если В (х)=0, то уравнение называется однородным; если В (х) 0 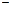неоднородным. Общее решение однородного уравнения получается путем разделения переменных; общее решение неоднородного уравнения получается из общего решения соответствующего однородного уравнения с помощью вариации произвольной постоянной интегрирования С.

Данное неоднородное уравнение можно интегрировать также с помощью замены у = uv, где u, v – две неизвестные функции.

3. Дифференциальное уравнение n – го порядка, разрешенное относительно производной, имеет вид 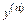= f (х, у, у′,…, ).

Задача нахождения решения у = 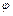(х) данного уравнения, удовлетворяющего начальным условиям 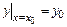; ; ; …; 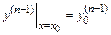, называется задачей Коши.

Для нахождения частного решения иногда используют так называемые краевые условия. Эти условия (их число не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка. Краевые условия ставятся лишь для уравнений порядка выше первого.

4. Теорема существования и единственности решения задачи Коши. Если в уравнении 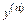= f (х, у, у ′, …, ) функция f (х, у, у ′,…, ):

a) непрерывна по всем своим аргументам х, у, у ′, …, в некоторой области D их изменения;

б) имеет ограниченные в области D частные производные 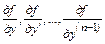по аргументам у, у ′, … , то найдется интервал h < х < + h (h > 0), на котором существует единственное решение у = 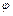(х) данного уравнения, удовлетворяющее условиям у ()= 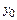; у ′()= ; …; , где значения х = ; у = 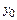; у ′= ; …; содержатся в области D.

Проинтегрировать (в конечном виде) уравнение n– го порядка можно только в некоторых частных случаях.

5. Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид 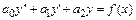, где числа, причем 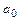≠0. Если f (х) = 0, то уравнение называется однородным, а если f(х)≠ 0 – неоднородным.

6. Квадратное уравнение называется характеристическим уравнением дифференциального уравнения . Пусть D = дискриминант квадратного уравнения. Возможны следующие случаи:

1) D >0 – общим решением уравнения является функция ( 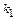и 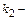корни характеристического уравнения);

2) D =0 – общим решением служит функция у = 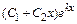(k –корень характеристического уравнения);

3) D <0–общим решением является функция ( 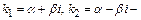корни характеристического уравнения).

7. Решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме.

Теорема. Если некоторое частное решение неоднородного уравнения = f (х)и Y –общее решение соответствующего однородного уравнения , то общее решение неоднородного уравнения имеет вид у = Y + у *.

Укажем правило нахождения частного решения неоднородного уравнения методом неопределенных коэффициентов.

1) Пусть f (х)= 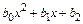; тогда:

а) у *= , если нуль не является корнем характеристического уравнения;

б) у *= , если нуль является простым корнем характеристического уравнения;

в) у *= 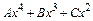, если нуль является двукратным корнем характеристического уравнения.

2) Пусть f (х)= 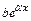; тогда:

а) у *= 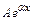, если число не является корнем характеристического уравнения;

б) у *= 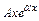, если число является корнем характеристического уравнения;

в) у *= 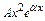, если число является двукратным корнем характеристического уравнения.

3) Пусть f (х)= 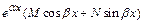; тогда:

а) у *= , если число 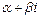не является корнем характеристического уравнения;

б) у *= 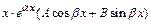, если число 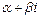является корнем характеристического уравнения.

Пример 1. Найти общее решение уравнения ху + + ху ′=0 и частное решение, удовлетворяющее начальному условию у (1)=2.

Решение. Перепишем данное уравнение так: 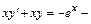и рассмотрим однородное уравнение х (у ′+ у)=0. Так как х ≠0 (значение х =0 не является решением неоднородного уравнения), то 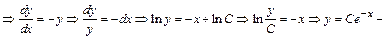общее решение однородного уравнения.

Применяем далее метод вариации произвольной постоянной С. Общее решение неоднородного уравнения будем искать в виде у = С (х) ;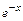

у ′=С′(х) 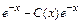. Подставив значения у и у ′ в неоднородное уравнение, получим

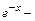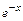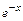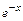
хС ′(х) хС (х) + хС (х) = х 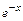С (х)= .

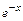Так как 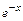≠0, то

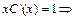
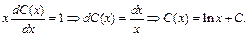
Подставив это значение С (х) в общее решение неоднородного уравнения, получим у =(ln х + С) 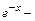общее решение неоднородного уравнения.

Для нахождения частного решения подставим значения х =1, у =2 в общее решение: у (1)=2 2=(0+ С) 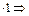С =2. Значит у =(ln х +2) 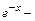частное решение неоднородного уравнения.

Пример 2. Найти общее решение уравнения 2 ху ′′′= у ′′ и частное решение, удовлетворяющее начальным условиям у (1)= 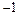; у ′(1)=0; у ′′(1)=1.

Решение. Пусть у ′′= z. Имеем 2 хz ′ 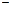z =0

Но z = у ′′ 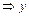′′= 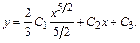Следовательно, у = 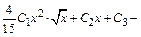общее решение дифференциального уравнения.

Чтобы найти частное решение, подставим в выражения для у, у ′ и у ′′ значение х =1:

;

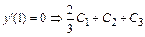=0;

Из системы уравнений 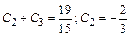находим 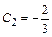; . Значит, искомое частное решение имеет вид:

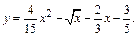
Пример 3. Найти общее решение уравнения y ′′ 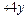′+13 у =5sin2 х и частное решение, удовлетворяющее начальным условиям = 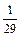при х =0.

Решение. Рассмотрим однородное уравнение y ′′ 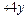′+13 у =0. Соответствующее характеристическое уравнение имеет вид +4 k +13=0, откуда 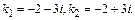Следовательно, Y =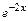 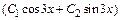общее решение однородного уравнения.

Частное решение неоднородного уравнения будем искать в виде

у *= 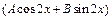. Имеем:

(у *)′= 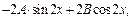(у *)′′= .

Подставим эти выражения в неоднородное уравнение

(9 А +8 В)cos2 х +(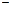 8 А +9 В)sin2 х =5sin2 х

и получим систему для вычисления коэффициентов А и В:

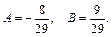
Итак, частное решение неоднородного уравнения имеет вид:

у *=

а общее решение неоднородного уравнения – вид

у =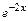

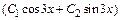
Найдем частное решение, удовлетворяющее заданным начальным условиям:

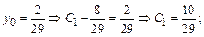
y= +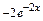

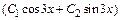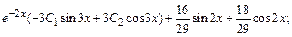
Искомое частное решение таково:

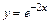
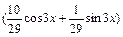
Дата добавления: 2014-11-16