
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула полной вероятности и формула Байеса
|
|
|
|
УЧЕБНИК АНГЛИЙСКОГО ЯЗЫКА
Александр Сергеевич ГЛЕБОВСКИЙ, Татьяна Алексеевна ДЕНИСОВА
Степени сравнения прилагательных и наречий (Degrees of comparison of adjectives and adverbs) 242
3.1 Образование степеней сравнения (Formation of degrees of comparison) 242
3.2 Сравнительные обороты (Comparative structures) 243
4 Числительные (Numerals) 244
4.1 Количественные числительные (Cardinals) 244
4.2 Порядковые числительные (Ordinals) 244
4.3 Даты (Dates) 244
4.4 Номера телефонов, страниц, комнат и т.д. (Phone, page, room numbers) 245
4.5 Дробные числа (Fractions) 245
5 Местоимение (Pronoun) 245
5.1 Личные, притяжательные и возвратные местоимения. 245
(Personal, possessive & reflexive pronouns) 245
5.2 Неопределённые и отрицательные местоимения. 246
(Indefinite & negative pronouns) 246
6 Глагол (Verb) 247
6.1 Типы глаголов. 248
6.2 Личные формы глагола. 249
6.3 Модальные глаголы (Modal verbs) 255
6.4 Согласование времён (Sequence of tenses) 257
6.5 Сослагательное наклонение (Subjunctive mood) 258
7 Неличные формы глагола (Verbals) 259
7.1 Инфинитив (The Infinitive) 259
7.2 Причастие (The Participle) 263
7.3 Герундий (The Gerund) 268
8 Словообразование (Word Formation) 271
8.1 Конверсия (Conversion) 271
8.2 Словообразовательные аффиксы (Derivational Affixes) 272
9 Структура предложения (Sentence Structure) 275
9.1 Утвердительное предложение (Declarative Sentence) 275
9.2 Вопросительное предложение (Interrogative Sentence) 276
9.3 Сложноподчиненное предложение (The Complex Sentence) 281
10 Приложение (Appendix) 282
10.1 Усилительные конструкции (Emphatic Constructions) 282
10.2 Многофункциональные слова (Multifunctional Words) 283
10.3 Неправильные глаголы.. 287
БИБЛИОГРАФИЯ ГРАММАТИКИ.. 289
Учебное издание
Под редакцией: Александра Сергеевича ГЛЕБОВСКОГО
для строительных вузов и факультетов по специальности промышленное и гражданское строительство
Часть I
Учебное пособие
Редактор А.В. Афанасьева
Корректор К.И.Бойкова
|
|
|
Компьютерная верстка И.А.Яблоковой
Подписано к печати Формат 60х80 1/16.Бум.офс.Усл.печ.л.
Уч.-изд.л..Тираж 1000 экз. Заказ «С»
Санкт-Петербургский государственный архитектурно-строительный университет.
198005, Санкт-Петербург, ул. 2-я Красноармейская, 4.
Отпечатано на ризографе. 198005, Санкт-Петербург, 2-я Красноармейская ул., 5.
Формула полной вер-сти явл.следствием обеих основных теорем.

(гипотезы)
Н1, Н2, …Нк – полная группа событий или разбиение Ω, если:
Н1+ Н2,+ …+Нк=Ω
Не пересекаются между собой
Hi*Hj=Ø i≠j I,j=1,2,…k
A=AH1+AH2+AH3+…+AHk (все слагаемые АНi несовместны)
Р(А)=Р(АН1+АН2+…+АНк)=Р(АН1)+Р(АН2)+…+Р(РНк)=Р(Н1)Р(А∕Н2)+…+Р(Нк)Р(А∕Нк)
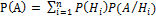 – формула полной вероятности.
– формула полной вероятности.
Формула Бейеса (теорема гипотез) явл.следствием теоремы умножения и формулы полной вер-сти. (необх-мо найти усл.вер-сть Р(Нi∕A) для каждой гипотезы.
Пр. Из какой урны более вероятно вытащить бел.шар? (Н1 или Н2)?
Р(Н1∕A) V Р(Н2∕A)
Р(Нi∕A)= 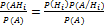 вычисл.по формуле полн.вер-сти
вычисл.по формуле полн.вер-сти
Дискретные сл.в. Ряд распределения. Числовые характеристики.
Ω= 
Случайная величина
X=X(Wi)числ.ф-ция, определенная на каждом элементарном исходе. (пространстве элем.соб.)
X1=X(W1)
X2=X(W2)
Случайная величина – величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Пр.
1) число попаданий при 3х выстрелах (0;1;2;3)
2) число вызовов, поступивших на телефон.станцию за сутки (1;2;3;4….)
3) частота попаданий при 10 выстрелах (0;0,1;0,2;….10)
дискретные – можно заранее перечислить
непрерывные – непрерывно заполняют некоторый промежуток.
Пр.
1) абсцисса точки попадания при выстреле;
2) ошибка взвешивания тела на аналитич.весах;
3) скорость летат.аппарата в момент выходп на заданную высоту;
4) все наугад взятого зерна пшеницы.
(границы неопределенные, расплывчатые)
Производится опыт соб.А – может появиться, а может и нет.
|
|
|
Вместо соб.А расмотр.сл.вел.Х, кот.=1
Если соб.А не происходит Х=0
Х – характеристическая сл.вел.соб.А
Х – сл.вел.
Х1,Х2….Хn – возможные значения сл.вел.Х
Ряд распределения
Закон распределения – всякое соотношение, устанавливающее связь между возможными значениями сл.вел-ны и соответствующими им вероятностями.
Простейшей формой задания закона распределения дисер.сл.вел.Х явл. таблица, в кто.перечислены возможные значения сл.вел. и соответствующие им вероятности.
1)  ряд распределения сл.вел.Х
ряд распределения сл.вел.Х
2)
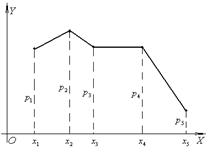 многоугольник распределения (один из форм закона распределения)
многоугольник распределения (один из форм закона распределения)
3)иногда удобной оказывается «механическая» интерпретация ряда распред-я (система матер.точек с какими-то массами, расп.на оси абсцисс)
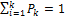
Числовые характеристики дискр.сл.величины
Числ.хар-ки – хар-ки, кот.характер-ют различн.св-ва случ-ной вел.
Характеристики положения
(мат.ожид-е, мода, медиана)
Указывают некоторые среднее ориентировочное значение, около которого группируются все возможные значения случ.вел.
1) Мат.ожидание - сумма произведений всех возможных значений сл.вел. на вероятности этих значений. 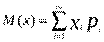
при большом числе опытов среднее арифмет.наблюденных значений сл.вел.приближается (сходится по вероятности) к ее матем.ожиданию.
М(Х) – абсцисса центра тяжести системы матер.точек.
Свойства М(х):
1)М(Х+а)=М(х)+а, а =const
2)М(аХ)=аМ(х)
3)М(Х+Y)=M(X)+M(Y)
4)h(X) – ф-ция Х, тогда 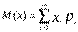
5) M(a)=a
2)Мода – наиболее вероятное значение (М)
3)Медиана: Р(Х 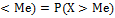
Моменты. Дисперсия. Среднее квадратическое отклонение.
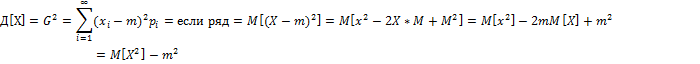
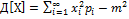 - определяет разброс отн-но
- определяет разброс отн-но  (хар-ка рассеивания)
(хар-ка рассеивания)

Дисперсия – мат.ожидание квадрата соответствующей центрированной величины.
Среднее квадратич.отклонение G= 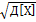
(для наглядной характеристики рассеивания)
Размерность совпадает с размеренностью сл.вел.
Свойства 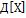 :
:
1) Неотрицательная 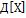 =0
=0
2) С-константа, 
3) 
4) 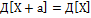
Моменты (опис.св-ва распр-я):
Начальные
dk

k=0,1,2….
d=1
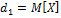 =m
=m
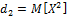
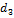 = хар-ка формы распределения
= хар-ка формы распределения
Центральные
Мк

M0 = 1
M1 = M 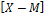 =0
=0
M2 = M 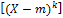 =Д
=Д 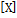
M3 - хар-ка формы распред-я
Хар-ка формы распределения:
Асимметрия
As(X)
As(X)= 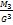
Эксцесс
Ех(Х)

Центрированная сл.вел. – отклонение сл.вел.Х от ее мат.ожид-я Х=Х-Мх
Повторение испытаний. Схема Бернулли. Биномиальное распределение. Формула Пуассона.
|
|
|
Один и тот же опыт повторяется соб.А может появиться или нет.
Нас интересует не результат каждого отдельного опыта, а общее число появлений соб.А в резте серии опытов.
Пр.число попаданий среди группы выстрелов.
Х~В(n1,p) – случ.вел.Х имеет биноминал.распр-е с параметрами n и p.
Схема Бернулли: (идеализир.ситуация) (если n=1)
Исходы эксперемента: «успех» (А)
«неуспех» (Ā)
К- число успехов в n исп-нии.
Р(А)=р
Р(Ā)=1-р=q
Эксперимент повторяется n раз, р и q не изменяются.
Рассм.случ.вел.Х – число успехов в n испытаний по схеме Бернулли.
Х=0,1,2,…n (целочисл.дискр.знач-я)

M(X)=n*p
Д(Х)=n*p*q
P(AA….A ĀĀ….Ā)=  (для конкр.посл-сти)
(для конкр.посл-сти)
Если n большое, то в силу ЦПТ В(n,p)  N(np;npq)
N(np;npq)
Если n большое, а 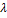 - фикс.число, то
- фикс.число, то 
Приближенная формула Пуассона
n – велико
p – мало
0,1  n*p
n*p  10
10
 где
где 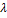 =n*p
=n*p
Док-во формулы 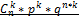


7
Распределение Пуассона. Геометрическое распределение.
Распределение Пуассона (Закон редких событий)
Дискр.сл.вел.Х=0,1,2,… имеет распр-е Пуассона с параметром 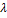 , если вероят-сть того, что она примет определение значения к, выражается формулой.
, если вероят-сть того, что она примет определение значения к, выражается формулой.

К=0,1,2,…
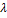 =n*p
=n*p

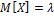

Редкое событие: стоим на перекрестке и подсчит.число столкновений.
Физич.модель, приводящ.к распределению Пуассона.
Поток событий – посл-сть некот.случ.соб-тий во времени.
Постулаты:
1) Поток явл. стационарным
2) Отсутствует последствие (т.е. без памяти)
3) Поток явл. ординарным
Вероятность того, что на интервале t произойдет к событий = 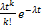
Поток явл. стационарным, если данная вер-сть произойдет независимо от времени.
Ординарность: можно найти столь малый интервал  , для которого вер-сть того, что на
, для которого вер-сть того, что на  произойдет 1 соб-е
произойдет 1 соб-е 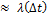 произойдет 2 и более событий
произойдет 2 и более событий  при
при 
Распр-е Пуассона играет ключ.роль в теории массового обслуживания.
Пр.
1) Поток входящих телефон.звонков;
2) Поломки оборудования;
3) Длит-сть исполнения ремонтных работ стабильно работающим сотрудником;
4) Ошибка печати;
5) Дефекты в длинной ленте или цепи.
Геометрическое распределение
p- вер-сть успеха
|
|
|
q- вер-сть неуспеха
p и q неизмен. Испытания независима дгур от друга.
Х – число эксперементов, кот. необх-мо произвести до появ-я 1-го успеха.
Х=1,2…..

K=1,2,3….
M 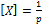
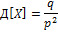
8
Непрерывные сл.вел. Функция распределения и плотность распределения и их свойства. Равномерное и экспоненц.распр-я.
Непрер.случ.вел. – числ.ф-ция, кот.задана на пространстве эл.событий.
Пример: время работы, время работы прибора.
Плотность распределения.
Берем еденич.массу и распределяем по мн-ву случ.вел.
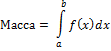
F(x) – плотность распр-ния массы (вероятностей)

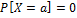
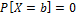
Свойства f(x):
1)ф-ция неотриц. f(x) 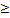 0
0
2) 
3) 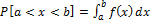
Функция распределения.

Свойства f(x):
1) 
2) 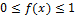
3) Механич. интерпретация f(x)
4) 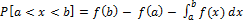
Равномерное распределение.
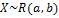 - интервал. (вероятность любого интервала зависит только от его длины)
- интервал. (вероятность любого интервала зависит только от его длины)
F(x)= 

Д(X)=M( 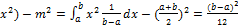
Применяется: ошибка округления.
Экспоненциальное распределение.
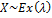 (моделирующее время между 2-мя последовательными свершениями одного и того же события)
(моделирующее время между 2-мя последовательными свершениями одного и того же события)



Пр.
1)время отказа аппаратуры;
2)время между 2ух последовательных покупателей;
3)время ожидания автобуса на остановке
(отсутствие памяти – кол-во времени, затрач.на ожидание автобуса, не влияет на время, кот.ему придется прождать)


Д(Х)= 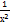
Ех( - частный случай распр-ния хи-квадрат
- частный случай распр-ния хи-квадрат
Свойства мат.ожидания и дисперсии. Квантили. Мода, медиана, асимметрия и эксцесс.

1) 
2) 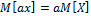
3) 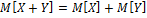
4) h(x) – ф-ция Х 
5) 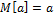
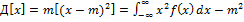
1) Неотриц. Д(х) 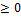
2) Д 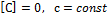
3) Д 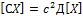
4) Д 
Квантиль
Пусть сл.вел.Х имеет f(x), F(x)
Квантилью порядка р(0  р
р  1) Хр назыв.абсцисса, кот.определяет от себя слева на графике плотности площадь = р.
1) Хр назыв.абсцисса, кот.определяет от себя слева на графике плотности площадь = р.

Способы определения квантили
1) 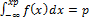
2) 
hx - квантиль порядка 0,5 (медиана)
Мода – значение, в котором плотность вероятности max.
Полимодальное распр.- более 1 max.
Антимодальное - посредине min.
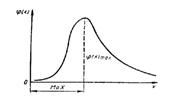
Медиана – значение, для которого одинаково вероятно, окажется ли сл.вел.меньше или больше hx.
Геом.медиана – абсцисса точки, в кот.площадь, огранич.кривой распределения делится пополам.
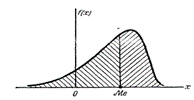
Хар-ка формы распределения.
Асимметрия

Хар-ка «скошенности» распределения

Экцесс

Хар-ет форму распр-я в окр-сти вершин (хар-ка «крутости»)

Если 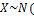 m,r)
m,r) 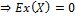
Нормальное распределение (Гаусса)
Вероятность попадания в интервал симметричный относительно М(х).
Ассиметрия и эксцесс распределения. Стандартизированное норм.распр-е и его свойство. Правило 3 сигм.


Явл.предельным законом, к котор.приближаются другие законы распр-я при весьма часто встречающихся типичных условиях.
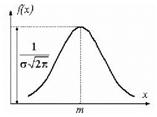
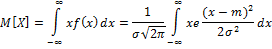
Замена: 
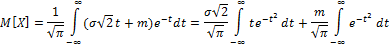
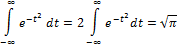
 - центр рассеивания. (особенно в задачах стрельбы).
- центр рассеивания. (особенно в задачах стрельбы).
Вероятность попадания в интервал.

Замена: 
X= 
dx= 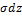
= 
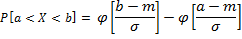
Свойства:
1) 
2) 
3) 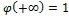
4) 
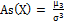 ;
; 



m=h=d

Стандартизованное нормальное распределение.
Стандартизация: 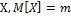

1 этап (центрированный): X-m

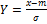 – стандартиз.сл.вел.
– стандартиз.сл.вел.
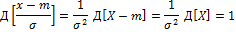
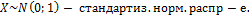
 x) – плотность распр-я.
x) – плотность распр-я.
 x)=
x)= 
Функция распр-я:  x)=
x)= 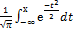
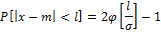

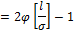
Правило 3 сигм: 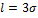
P 
Системы дискретных сл.вел.
Таблица распределения. Независимость. Ковариация. Условные распределения. Системы непрерыв.сл.вел.
Рез-т опыта описывается не 1 сл.вел., а 2умя или >сл.вел-нами, образующими комплекс или систему.
(напр.: точка попадания снаряда опр-тся абсциссой и ординатой)
При рассмотрении вопросов, связан.с сист.сл.вел.удобно пользоваться геом.интепретацией системы.
(напр.(X,Y) можно изобразить случайной точкой на плоскости с коорд-ми X и Y.
Часто вместо образа случ. точки пользуются образом случайного вектора.
(X,Y) – случ.вектор с коорд-ми
Х=Х1,Х2, …Хк
Y=Y1,Y2,…Yk - дискр.сл.вел.
 - закон распр-я для (X,Y)
- закон распр-я для (X,Y)

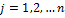

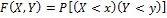
Ф-ция распр-я.
Y  X X
| X1 | X2 | … | XK | Σ |
| Y1 | P11 | P21 | … | PK1 | PY1 |
| Y2 | P12 | P22 | … | PK2 | PY2 |
| … | … | … | … | … | … |
| yn | P1n | P2n | … | Pkn | Pyn |
| Σ | Px1 | Px2 | … | Pxk |
Крайние маргинальные распределения.
Ру1*Рх1=Р11
X и Y независимы.
(если хотя бы 1 невыполн., то зависимы)
Условные распределения.
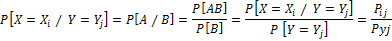
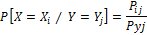

Независимость случ.вел-н.
(не завис.от того, какое значение приняла др.величина)
X и Y независ.сл.вел., если:
 , т.е.усл.вер-сть совпадает с безусловной.
, т.е.усл.вер-сть совпадает с безусловной.
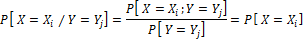

Если X и Y независимы, то 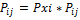 необх.и дост.усл-е независ-сти величин.
необх.и дост.усл-е независ-сти величин.
Ковариация.
Мат.ожидание произведения центрированных случ.величин.
Cov(X,Y)=M 
Cov(X,Y)= 
Свойство: если X и Y независимы, то 
(однако обратное неверно, т.е. если  , то не обязат.независ.)
, то не обязат.независ.)
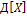

 - ковариац.мтр
- ковариац.мтр
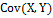 =
= 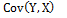
Системы непр.сл.вел.
Распр.системы непр.вел.обычно хар-ют не ф-цией распр-, а плотностью распр-я.
F(X,Y) – плотность распр-я
1) F(X,Y) 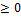
2) 

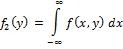
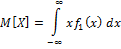

Мат.ожидание и дисперсия суммы сл.в. Мат.ожидание произв-я сл.в.
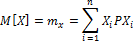
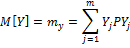
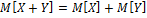
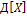
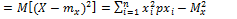

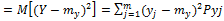
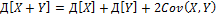
Если зависимы

Если независ.

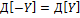
13
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 370; Нарушение авторских прав?; Мы поможем в написании вашей работы!