Условная вероятность. Независимость событий. Вероятность произведения событий. Теорема о полной вероятности. Формулы Байеса

Рассмотрим теоретическое определение вероятности.

Вероятностью называется действительная функция Р(А), заданная на множестве случайных событий некоторого испытания (опыта), имеющая следующие свойства:

1) Р(А) 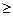0,

2) Р(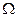) = 1,

3) Если события А и В несовместны, т. е. АВ = Æ, то

Р(А+В) = Р(А)+Р(В),

4) P_А(В) = ,

Для формулировки свойства 4) введем понятие условной вероятности P_А(В) события В при условии А. Ее можно определить как вероятность события В, вычисленную в предположении, что событие А произошло.

В связи со свойством 4) возникает важное понятие независимости событий: события А и В называются независимыми, если вероятность одного из них не зависит от того, произошло или нет другое. Другими словами, это означает, что Р (В)=Р_А(В) (или Р (А)=Р_В(А)).

Следствия:

Из определения получим следующие простейшие свойства вероятности:

1) Р( Æ ) =0;

2) Р(`А) = 1- Р(А);

3) Формула умножения вероятностей

РАВ)=Р(А)Р_А(В).

Эта формула получается непосредственно из свойства 4) вероятности.

Чтобы лучше понять смысл этой формулы, воспользуемся геометрическим определением вероятности. Итак, пусть А и В - случайные события.

W

A B

A.B

Обозначим через

S - площадь области W;

S_А - площадь А;

S_В - площадь В;

S_АB - площадь пересечения А и В.

Тогда для вероятности события АВ будем иметь:

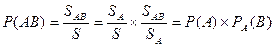
В этом равенстве Р (АВ) и Р (А) - обычные вероятности, а Р _А(В) - условная вероятность события В при условии А.

Формула умножения вероятностей для независимых событий принимает более простой вид:

Р(АВ) = Р(А)Р(В).

Если при вычислении Р (АВ) вопрос о независимости событий А и В является затруднительным, то рекомендуется пользоваться при этом первой, более общей формулой. Заметим также, что формула умножения вероятностей допускает обобщение на случай нескольких сомножителей:

для любых событий А₁, А₂,..., А_n

и

Р(А₁А₂...А_n) = Р(А₁)×Р(А₂)×...Р(А_n)

для независимых событий.

4) Формула сложения вероятностей

Р(А+В)=Р(А)+Р(В) – Р(АВ),

здесь события А и В могут быть совместными.

Рассмотрим случайные события А и В. Возможны два случая.

1. События А и В несовместны. Тогда, по определению получим,

р(А+В)=р(А)+р(В);

2. События А и В совместны.

W

A B

A+B

Проверим справедливость формулы с помощью геометрической интерпретации определения случайного события и вероятности. Для удобства будем считать, что площадь S(W)=1.

Тогда вероятность любого события численно будет равна площади соответствующей области. Поскольку площадь объединения А и В складывается из площадей А и В за вычетом площади их пересечения, то отсюда и следует формула сложения вероятностей совместных событий.

Аналогично можно получить формулу сложения вероятностей для суммы трех попарно совместных событий:

Р (А+В+С)=Р(А)+Р(В)+Р(С) - Р(АВ) - Р(ВС) - Р(АС)+Р(АВС).

Для вычисления вероятности суммы n ³ 3 удобнее пользоваться следующей формулой (вероятность наступления хотя бы одного из n событий А 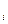, i = 1,…, n ):

Р(А₁+А₂+...+А_n) = 1 - Р(`А<sub>1</sub>`×А₂×...`А_n),

которая является следствием противоположности событий (А₁+А₂+...+А_n) и (`А<sub>1</sub>×`А₂×...`А_n).

Приведем примеры пространств элементарных исходов с введенной на них вероятностью случайного события.

1) Классическое определение вероятности.

Предположим, что для рассматриваемого испытания существует группа событий {A₁, A₂,..., A_n}, удовлетворяющая условиям:

1) события А_i попарно несовместимы, т.е. A_i×A_j =Æ для всех i 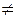j;

2) А₁ + А₂ +... + А_n = W, т.е. в результате испытания хотя бы одно из этих событий обязательно произойдет.

3) события А_i равновероятны в том смысле, что из двух событий А_i и А_j, i j одно не является более возможным, чем другое(это условие обеспечивается выбором предметов наугад, симметрией и т.п.)

Если эти условия выполняются, то говорят, что события 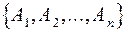образуют полную группу равновероятных и несовместных событий, а сами события А_i называют элементарными исходами, или просто исходами.

Рассмотрим теперь какое- то другое случайное событие А. Если при наступлении исхода А_i событие А обязательно произойдет, то этот исход А_i называется благоприятствующим событию А, в противном случае исход А_i называется неблагоприятствующим событию А. Пусть m - число элементарных исходов, благоприятствующих событию А (напомним, что n - это общее число всех исходов). Классической вероятностью события А называется число

P(A) =

Рассмотрим для начала несколько простейших примеров вычисления вероятностей по классическому определению.

Задача 1. Найти вероятность того, что при одном бросании игральной кости (кубика) выпадет четная цифра большая 3.

Решение: Рассмотрим следующие элементарные исходы:

А₁ - на кубике выпала цифра “1”;

А₂ - на кубике выпала цифра “2”;

...

...

А₆ - на кубике выпала цифра “6”.

Исходы А₁… А₆ образуют полную группу несовместных и равновероятных исходов (равновероятность - следствие симметрии кубика). Событию А, описанному в задаче, благоприятствует два исхода: А₄ и А₆. Таким образом, n = 6, m = 2, а поэтому

p(A) =

Замечание. Предположим, что в этой задаче мы имели бы дело с кубиком неправильной формы (например, похожим на спичечный коробок). В таком случае условие равновероятности исходов было бы явно нарушено, что привело бы к невозможности использовать классическое определение вероятности (тогда, как было замечено ранее, вероятность p(А) можно найти лишь статистически).

Задача 2. Из набора костей домино наугад извлекают одну кость. Какова вероятность того, что эта кость - дупль.

Решение: В полном наборе костей домино - 28 штук, из них - 7 дуплей. Полную группу равновероятных и несовместных исходов образуют 28 исходов, 7 из которых благоприятствуют рассматриваемому событию А. Таким образом,

p(A) = .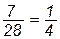

Задача 3. Из колоды в 36 карт наудачу достают одну карту. Найти вероятность того, что эта карта - туз.

Решение: Эта задача по своей сути практически не отличается от предыдущих двух. Поэтому приведем очень краткое решение (студенту рекомендуется придумать его самостоятельно).

n=36, m=4, p(A) = .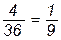

Дата добавления: 2014-11-16