Числовые характеристики дискретных случайных величин. Математическое ожидание, его свойства. Дисперсия и среднеквадратическое отклонение, основные свойства и вычисление

Рассмотрим ДСВ Х, заданную своим законом распределения:

Х	х1	х2	х3	….	хn
Р	р1	р2	р3	….	рn

Математическим ожиданием этой ДСВ Х называется число М(Х), которое определяется следующим образом:

М(Х)=х₁р₁+х₂р₂+…+х_nр_n

(если множество значений Х бесконечно, то вместо конечной суммы берется числовой ряд ).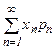

Перечислим некоторые свойства математического ожидания.

1. М(С)=С, где С – постоянная;

2. М(С×Х)=С×М(Х);

3. М(Х+У)=М(Х)+М(У);

4. М(ХУ)=М(Х)×М(У), если Х и У – независимы;

Дисперсией ДСВ Х называется число:

D(Х)=М(Х – М(Х))²=S(x_k– М(Х))²×p_k.

Следствие:

D(Х)=М(Х²) – М²(Х).

1. Д(С)=0, где С – постоянная;

2. Д(X) ³ 0;

3. Д(С×Х)=С²Д(Х);

4. Д(Х ± У)=Д(Х)+Д(У), если Х и У – независимы;

Рассмотрим вероятностный смысл математического ожидания и дисперсии. Вспомним для этого статистическое определение вероятности. Предположим, что некоторое испытание проведено многократно (N раз) и при этом ДСВ Х приняла:

Значение х₁ – N₁ раз;

Значение х₂ – N₂ раз;

…

Значение х_n – N_n раз.

Тогда для любого 1£k£n имеем, с одной стороны, Р(Х=х_k)=р_k (из закона распределения), а, с другой стороны, Р(Х=х_k)»N_k/N (исходя из статистического определения вероятности). Таким образом, р_k »N_k/N для любого k. Если теперь рассмотреть среднее значение `Х ДСВ Х в этой серии из N испытаний, то получим:

`X= 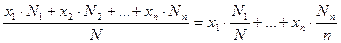»х₁p₁+x₂p₂+…+x_np_n=M(X).

Таким образом, можно сделать следующий вывод: математическое ожидание М(Х) ДСВ Х практически совпадает со средним значением `Х этой случайной величины за достаточно большое число испытаний, т.е.

М(Х)»`Х.

Аналогичный вывод можно сделать и для дисперсии, т.к. она определяется через математическое ожидание. Выражаясь не вполне строго, можно сказать, что дисперсия D(Х) характеризует разброс значений ДСВ Х относительно ее среднего значения. Более точной характеристикой величины этого разброса является среднеквадратическое отклонение:

s=

Рассмотрим на примерах построение законов распределения ДСВ и нахождения их числовых характеристик.

Задача 1. Бросают два кубика. Случайная величина Х – это разность (по модулю) между двумя выпавшими цифрами. Найти закон распределения Х, а также М(Х), D(Х), и s(Х).

Решение. Очевидно, что Х может принимать любые значения от 0 до 5. Для любого k=0, 1, 2, 3, 4, 5 вероятность Р(Х=k) можно найти по классическому определению. Общее число исходов n=36, запишем все исходы в виде таблицы.

(1,1)	(1,2)	(1,3)	…	(1,6)
(2,1)	(2,2)	(2,3)	…	(2,6)
(3,1)	(3,2)	(3,3)	…	(3,6)
…				…
(6,1)	(6,2)	…		(6,6)

Найдем вероятности:

Р(Х=0)=6/36 (этому событию соответствует 6 исходов, стоящих на главной диагонали);

Р(Х=1)=10/36 (10 исходов, стоящих на двух побочных диагоналях);

… и т.д.

В результате получим следующий закон распределения:

Х	0	1	2	3	4	5
Р	6/36	10/36	8/36	6/36	4/36	2/36

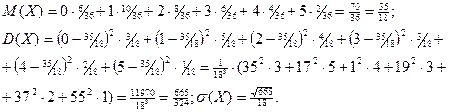
Задача 2. В урне находится 6 белых шаров и 4 черных. Из урны берут наугад два шара. Случайная величина Х – это число белых шаров среди двух выбранных. Найти М(Х) и D(Х).

Решение. ДСВ Х может принимать значения 0, 1 или 2. Их вероятности находим по классическому определению:

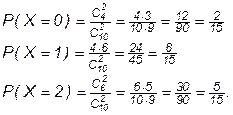
Значит, закон распределения Х имеет вид:

Х	0	1	2
	Р	2/15	8/15	5/15

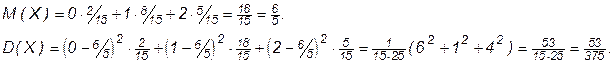
Операции над случайными величинами

Рассмотрим ДСВ Х, заданную своим законом распределения:

Х	х1	х2	…	хn
Р	p1	p2	…	pn

Если С – некоторое постоянное число, то можно рассмотреть другую случайную величину Z=СХ, закон распределения которой имеет следующий вид:

СХ	Сх1	Сх2	…	Схn
Р	p1	p2	…	pn

Можно также рассмотреть случайную величину Z=Х². Ее закон распределения имеет вид:

Х^2	х1^2	х2^2	…	хn^2
Р	p1	p2	…	pn

При этом в верхней строке могут оказаться пары одинаковых значений, которые следует объединить, сложив при этом соответствующие вероятности. Рассмотрим простой пример.

Задача. Задан закон распределения ДСВ Х. Найти М(Х²).

Х	-1	0	1	2
Р	0,1	0,4	0,3	0,2

Решение. Составим закон распределения Х².

Х^2	(-1)^2	0^2	1^2	2^2
Р	0,1	0,4	0,3	0,2

Первое и третье значения у Х² оказались одинаковыми ((- 1)²= 1²), поэтому окончательно получим:

Х^2	0	1	4
Р	0,4	0,4	0,2

Таким образом, М(Х²)=0×0,4+1×0,4+4×0,2=1,2.

Рассмотрим теперь две случайные величины Х и У, связанные с одним и тем же испытанием. В этом случае можно рассмотреть случайную величину Z=Х+У. Предположим, что Х и У – независимые случайные величины, т.е. вероятность принятия одной из них какого-либо значения не зависит от того, какое значение приняла другая. Покажем, как в таком случае составить закон распределения суммы Х+У, если известны законы распределения слагаемых:

Х	х1	х2	…	хn
Р	p1	p2	…	Pn

У	у1	у2	…	Уm
Р	q1	q2	…	qm

По формуле умножения вероятностей для независимых событий:

P(X=x_i, Y=y_j)=P(X=x_i)×P(Y=y_j)=p_iq_j

Поэтому мы получим закон распределения суммы Х+У, если в верхней строке выпишем всевозможные суммы x_i+y_j (их число должно быть в точности равно mn согласно правилу произведения), а в нижней строке – соответствующие им вероятности p_iq_j. Если при этом некоторые значения в верхней строке окажутся повторяющимися, то одинаковые значения надо объединить, сложив соответствующие им вероятности.

Аналогично можно построить закон распределения произведения ХУ двух независимых случайных величин.

Рассмотрим более подробно эту задачу на следующем примере.

Задача. Имеются две урны с шарами: в первой урне 3 белых шара и 2 черных, а во второй – 1 белый и 4 черных. Из каждой урны достают наугад по два шара. Рассмотрим две случайные величины: Х – это число белых шаров, вынутых из первой урны, а У – число белых шаров, вынутых из второй урны. Найти законы распределения случайных величин Z₁=Х+У и Z₂=ХУ.

Решение. Случайная величина Х может принимать любое из трех значений: 0, 1, 2. Вероятность каждого из них находим по классическому определению.

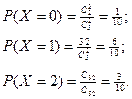
Случайная величина У может принимать только два значения: 0; 1.

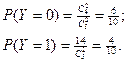
Таким образом, мы получаем законы распределения Х и У.

Х	0	1	2	Y	0	1
Р	0,1	0,6	0,3	Р	0,6	0,4

Легко понять, что случайные величины Х и У – независимы. Поэтому их сумма Х+У будет иметь следующий закон распределения:

Х+Y	0+0=0	0+1=1	1+0=1	1+1=2	2+0=2	2+1=3
Р	0,1×0,6=0,06	0,1×0,4=0,04	0,6×0,6=0,36	0,6×0,4=0,24	0,3×0,6=0,18	0,3×0,4 =0,12

или, объединяя второй столбец с третьим, а четвертый с пятым, окончательно получим:

Х+Y	0	1	2	3
Р	0,06	0,4	0,42	0,12

Аналогично для случайной величины ХУ получим

ХY	0×0=0	0×1=0	1×0=0	1×1=1	2×0=0	2×1=2
Р	0,06	0,04	0,36	0,24	0,18	0,12

Объединяя первый, второй, третий и пятый столбцы, окончательно будем иметь:

ХY	0	1	2
Р	0,64	0,24	0,12

Задача. Наугад выбирают число 2£n£10 (целое), а затем раскладывают его в произведение простых сомножителей. Случайная величина Х – это число сомножителей в этом разложении. Найти Д(Х).

Решение. Общее число исходов данного испытания равно 9.

Р(Х=3)=1/9 (соответствует одному исходу: 8=2×2×2);

Р(Х=2)=4/9 (соответствует четырем исходам: 4=2×2; 6=2×3; 9=3×3; 10=2×5);

Р(Х=1)=4/9 (соответствует четырем исходам: 2, 3, 5, 7 – простые числа).

Запишем законы распределения Х и Х²:

Х	1	2	3	Х^2	1	4	9
Р	4/9	4/9	1/9	Р	4/9	4/9	1/9

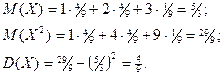
5. Числовые характеристики непрерывных случайных величин. Математическое ожидание, его свойства. Дисперсия и среднеквадратическое отклонение, основные свойства и вычисление.

Рассмотрим НСВ Х, имеющую плотность распределения f(x). Математическое ожидание М(Х) и дисперсия D(Х) этой случайной величины определяется следующим образом:

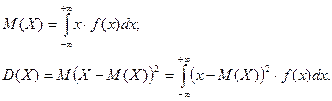
Используя определение определенного интеграла как предела интегральных сумм

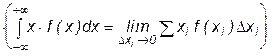и вероятностный смысл плотности распределения f(x_i) 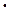Dx_i» p_i, можно показать, что эти определения является обобщением на случай НСВ определений математического ожидания и дисперсии ДСВ.

В частности, отсюда следует, что М(Х) и Д(Х) для непрерывных случайных величин имеет тот же самый вероятностный смысл, что и для дискретных, т.е. М(Х) характеризует среднее значение НСВ Х за достаточно большое число испытаний, а D(Х) – среднее значение квадрата отклонения Х от М(Х).

Задача 1. Случайная величина Х задана своей плотностью распределения

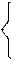
k(x-x²), если 0£ х£ 1;

f(x)=

0, в противном случае.

Требуется:

1. найти коэффициент k;

2. найти функцию распределения F(x);

3. построить схематически графики функций f(x) и F(x).

4. найти математическое ожидание М(Х), дисперсию D(x) и среднеквадратическое отклонение s (Х);

5. найти вероятность попадания Х в интервал (1/3; 1/2),

Решение.

1)Коэффициент k найдем из условия нормировки: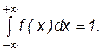

Имеем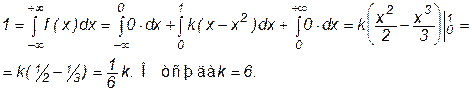

2)

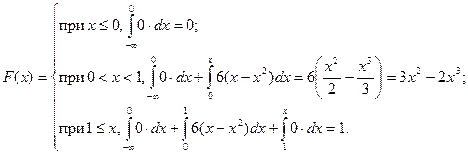
3) Графики функций f(x) и F(x) имеют вид:

y y

y=f(x) y=F(x)

1

x x

1 1

4)

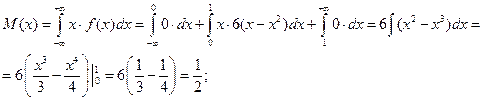
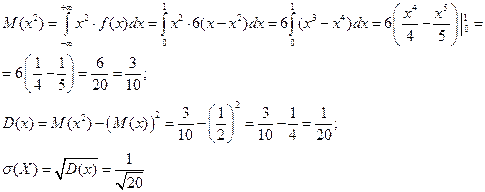
5)

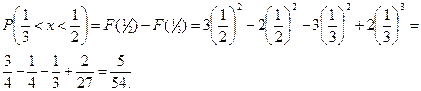
Задача 2. Случайная величина Х задана своей функцией распределения:

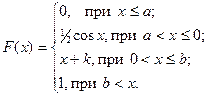
Требуется найти:

1. плотность распределения f(x);

2. М(Х);

3.

Решение. В условии задачи не указаны значения параметров a, b и k. Их можно найти из условия непрерывности функции распределения F(x). Схематично изобразим график y=F(x).

y

y=F(x) a=-p/2

k=1/2

1 b=1/2

1/2

-p/2 1/2

Теперь найдем плотность распределения f(x)=F’(x).

y 0, если х£ -p/2

y=f(x) f(x)= -1/2sinх, если p/2<х£0

1 1, если 0<х£1/2

0, если x>1/2

-p/2 1/2 x

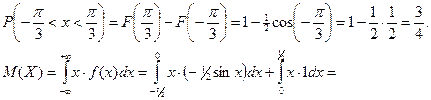
(1-й из этих интегралов берется по частям, а 2-й — табличный)

Дата добавления: 2014-11-16