Предельные теоремы Муавра-Лапласа

Рассмотрим снова схему Бернулли, т.е. последовательность независимых испытаний с двумя исходами в каждом (успех или неудача). Напомним обозначения: р – вероятность успеха, q=1-р – вероятность неудачи, n – общее число испытаний, случайная величина К – это число успехов в этой серии испытаний, Р_n(k) – вероятность того, что число успехов в этой серии будет равно в точности k. Пусть n – достаточно большое число.

Прежде всего заметим, что, т.к., , то каждая из вероятностей Р_n(k) при больших n очень мала. Поэтому при больших n целесообразно несколько изменить постановку задачи, а именно, найти вероятность того, что число успехов k в этой серии будет заключено между m₁ и m₂, т.е.

Р(m₁£k £m₂),

где m₁ и m₂ – заданные числа.

Рассмотрим для последовательность случайных величин Х₁, Х₂, …, Х_n, каждая из которых определяется следующим образом:

1, если в k -ом испытании был успех

X_k=

0, если в k- ом испытании была неудача

Все эти случайные величины имеют одинаковый закон распределения:

Хk	0	1
Р	q	p

Поэтому

М(Х_k)=0q+1p=p;

D(X_k)=M(X_k²)-(M(X_k))²=0q+1p-p² = p-p²=pq.

Интересующая нас случайная величина K является суммой Х₁, Х₂, …, Х_n:

K= X₁+X₂+…+X_n.

Значит

М(К)=M(X₁)+M(X₂)+…+M(X_n)=np;

D(K)=D(Х₁)+D(Х₂)+…+D(Х_n)=npq;

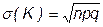
Оказывается, что имеет место удивительный факт: при достаточно больших n случайная величина К имеет распределение, близкое к нормальному, так как имеет место следующая

Теорема. (Центральная предельная теорема Ляпунова.) Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

На практике для большинства случайных величин выполняются условия теоремы Ляпунова.

В нашем случае, можно предположить, что вероятность

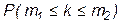
- близка к вероятности попадания НРСВ с параметрами а=np и 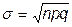в интервал 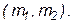Если воспользоваться формулой (см.с.31), выражающей эту вероятность через функцию Лапласа, то получим интегральную формулу Муавра-Лапласа:

Вместо случайной величины К рассматривают также относительную частоту появления успехов в серии. При достаточно больших n относительная частота близка к вероятности p. Разность 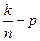равной 0 практически не бывает, а отклонение от p на небольшое число e>0 возможно, поэтому найдем вероятность выполнения неравенства

|k/n – p|< .

или

P(np – n <k<np+n )

Эту вероятность найдем, применяя интегральную формулу Муавра-Лапласа:

=

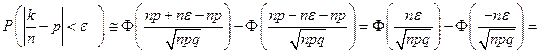
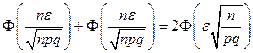
Итак:

.

Задача. Производится серия из n=2500 независимых испытаний с вероятностью успеха в одном испытании р=0.8 (значит, q=0,2 – вероятность неудачи). Требуется:

1. Найти вероятность того, что число успехов k во всей серии окажется в пределах от 1970 до 2010;

2. Найти вероятность того, что число успехов не превысит 2025;

3. Найти вероятность того, что относительная частота успехов во всей серии будет отличаться от вероятности успеха Р по модулю не более, чем на 0,02;

4. Какое отклонение относительной частоты успехов от вероятности успеха по модулю можно ожидать с вероятностью 0,9;

5. Какое минимально число испытаний нужно произвести, чтобы с вероятностью не менее, чем 0,95 можно было утверждать, что отклонение относительной частоты успехов от вероятности успеха по модулю не превысит 0,01.

Решение. np=2000; =0.4; =50.

1. P(1970 k 2010)= F(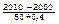) –F ()=

=F (0.5) –F (-0.5)= F(0.5)+ F(1.5)=0.1915+0.4332=0.6247

2. P(k 2025)@ F()+1/2=F (1.25)+0.5=0.3944+0.5=0.8944

3. P(|k/n–p|<0.02) @2F ()=2F (2.5)=2*0.4938=0.9876

4. P(|k/n–p|<e)@2F (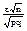)=0.9

Отсюда F ()=0,45. Теперь по таблице находим значение х, при котором F (х)=0,45. Это будет х=1,645. Значит, =1,645, откуда e=0,01316.

5. P(|k/n–p|<0.01) @2F()=0.95. По таблице находим, что F(1,96)=0,475. Поэтому =1,96, откуда находим n=(0,4×1,96×100)²=6147.

Дата добавления: 2014-11-16