Из последнего равенства аналогичным образом для некоторого целого неотрицательного s получаем 4 страница

С другой стороны, у 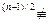1 (mod n). Действительно,

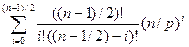
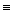у = (1+ n / p) = 1 + 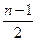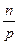(mod n)

(остальные члены в биноме Ньютона кратны n). Таким образом, если бы левая часть была равна 1 по модулю n, то выполнялось бы сравнение

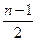
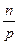
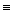0 (mod n).

А это возможно лишь при условии, что р | (n – 1)/ 2, что невозможно, ибо p | n.

Тест Соловея-Штрассена. На последней теореме основан вероятностный тест на простоту, который выдерживают простые числа с вероятностью 1, а составные – с вероятностью менее ½. Время работы оценивается величиной О(log n), где n – тестируемое число.

Вход: нечетное n.

1. Выбрать случайное х такое, что 1 < x < n- 1.

2. Если 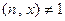, то прекратить работу с резолюцией «составное». Иначе продолжать.

3. Если x (mod n), то остановиться с резолюцией «составное», иначе остановиться с резолюцией «простое».

Определение. Пусть n – нечетное составное число, и пусть n – 1 = 2 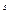t, где число t является нечетным. Пусть b Z 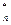. Если числа b и n связаны условием

b 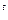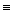1 (mod n) или

существует число r, 0 r < s, такое, что b 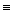-1 (mod n), (6.4)

то число n называется сильно псевдопростым по основанию b.

Пример. Примерами сильно псевдопростых чисел являются:

– сильно псевдопростое по основанию 7;

781 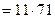– сильно псевдопростое по основанию 5;

2047 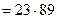– сильно псевдопростое по основанию 2.

Теорема. Если n 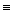3 (mod 4), то число n является сильно псевдопростым по основанию b тогда и только тогда, когда является псевдопростым Эйлера по основанию b.

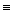
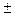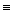
Доказательство. Учитывая, что в этом случае s = 1, t = (n -1)/2, видим, что число n есть сильно псевдопростое по основанию b тогда и только тогда, когда b 1 (mod n). Если теперь n есть псевдопростое Эйлера, то это сравнение следует из опре-деления. Обратно, допустим, что b 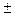1 (mod n). Надо показать, что 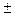1 в пра-вой части равно . Но для n 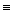3 (mod 4) имеем: 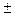1 = 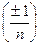и, следовательно,

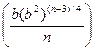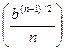
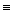= = b (mod n),

что и требовалось доказать.

Теорема. Если n есть сильно псевдопростое число по основанию b, то оно является и псевдопростым числом Эйлера по основанию b.

Замечание. Утверждение, обратное теореме, неверно.

Теорема. Если n есть нечетное составное число, то n является сильно псевдопростым по основанию b для не более чем 1/4 таких оснований, где 0 < b < n.

Тест Миллера-Рабина. На последней теореме и понятии сильно псевдопростого числа основан тест на простоту, который с вероятностью 1 подтверждает простоту числа и с вероятностью менее ¼ ошибается, называя простым число составное. Время работы этого теста оценивается величиной О(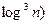, где n – тестируемое число.

Вход: n – нечетное натуральное число, 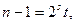где 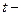нечетное.

1. Выбрать случайное х такое, что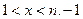

2. Если ( то остановиться с резолюцией «n – составное», иначе

продолжать.

3. Вычислить

4. Если 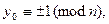то остановиться с резолюцией «простое», иначе

продолжать.

5. Вычислять пока не выявится, что , .

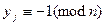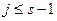6. Если 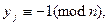то остановиться с резолюцией “простое”, а иначе – остановиться с резолюцией «составное».

Замечания:

1. При проверке чисел на простоту не всегда нужно ожидать, если есть подозрение, что проверяемое является сильно псевдопростым, что придется иметь дело с очень большими основаниями, по которым это число и является сильно псевдопростым. Например, вычислено, что для чисел не больших 2,5 существует лишь одно число, а именно 3215031751, которое является сильно псевдопростым по основаниям 2,3,5 и 7. Можно привести и другие результаты такого рода, скажем, если и проходит тест Миллера-Рабина по основаниям 2, 3, 5, 7, 11, и 13, то n – простое; если и проходит тест Миллера-Рабина по основаниям 2, 13, 23 и 1662803, то n – число простое.

2. Вероятностные тесты на простоту не дают полной уверенности в том, что число, прошедшее тест, действительно простое. Желательно иметь, например, такой результат: существует некоторое сравнительно небольшое число В (зависящее от n) такое, что если n – составное, то существует определенное основание b < B, для которого число n не является сильно псевдопростым. Тогда применение вероятностного теста Миллера-Рабина только для первых В оснований вычислительно доказывало бы простоту числа n или противоположное утверждение.

Такой результат известен, но он зависит от недоказанной пока т.н. расширенной гипотезы Римана (РГР). Его можно сформулировать так:

Теорема (Миллер). Если справедлива РГР и n – составное нечетное число, то n не проходит тест Миллера-Рабина для по крайней мере одного основания b, где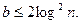

3. В 1986 г. С Голдвассер и Дж. Килиан предложили вероятностный алгоритм, основанный на теории эллиптических кривых, работающий, как ожидается, за полиномиальное время на почти всех входах.

Общая схема построения простого числа заданного размера выглядит так: Выбирается случайное натуральное число n такое, что 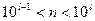. Это число проходит проверку на делимость на «малые» простые числа, т.е. на числа 2, 3, 5, 7 и т.д. Массив «малых» простых чисел может быть весьма значительным по размеру. Затем наступает очередь вероятностных тестов. Они работают быстро и могут выявить, что испытуемое число является составным. Если, например, тест Миллера-Рабина принимает вход при некотором количестве испытаний, то наступает черед детерминированных тестов, которые дадут окончательный ответ. Продемонстрируем один из возможных способов построения большого простого числа, на основании уже имеющегося простого.

3. Один метод построения простых чисел.

Метод основан на модифицированной теореме Ферма.

Теорема. Пусть – нечетные натуральные числа, 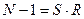, причем для каждого простого делителя q числа S существует целое число а такое, что

.

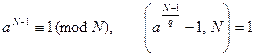Тогда каждый простой делитель р числа N удовлетворяет сравнению .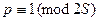

Доказательство. Пусть р – простой делитель числа N, а q – некоторый простой делитель S. Из условий теоремы следует, что в поле F 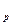справедливы соотношения

Обозначим через r порядок элемента а в F 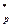. Первые два из последних соотношений означают, что q входит в разложение на простые множители числа r в такой же степени, как и в разложение N -1, а последнее – что р -1 делится на r. Таким образом, каждый простой делитель числа S входит в разложение р -1 в степени не меньшей, чем в S. Значит, р -1 делится на S. Для завершения доказательства заметим, что р -1 четно.

Следствие. Если выполнены условия теоремы и , то N – простое число.

Действительно, если N равняется произведению не менее двух простых чисел, то каждое из них, согласно утверждению теоремы, не меньше 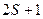. Но тогда

.

Противоречие доказывает следствие.

Пусть теперь известно некоторое простое число S. Опираясь на него, будем строить новое простое число N. Выберем для этого случайное четное число R в промежутке 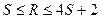и положим . Протестируем число N на простоту путем деления на малые делители и вероятностными тестами. Если при этом выявится, что N составное, то следует выбирать новое число R и повторить вычисления. Если такого не произошло, то можно попытаться доказать простоту N при помощи приведенной выше теоремы. Для этого случайным образом выбирают число а, 1 < a < N, и проверяют для него выполнимость соотношений:

.

Если выбранное а удовлетворяет указанным соотношениям, то по следствию из последней теоремы число N – простое. Если соотношения не выполняются, то следует выбирать другое число а,и так до тех пор, пока соответствующее, а не будет найдено.

Если число 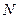действительно простое, то учитывая, что сравнение

имеет не более 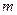решений, можно утверждать, что вероятность попасть на подтверждающее простоту 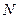число а не менее

, где с – положительная константа.

4. Некоторые задачи.

Задача 1. Найти все основания b, по которым 15 является псевдопростым числом. (Не принимать во внимание тривиальные основания .

Задача 2. Показать, что если одновременно р и 2 р – 1 являются простыми числами и n = p (2 p – 1), то число n является псевдопростым для 50% возможных оснований, именно: для всех b, которые являются квадратичными вычетами по модулю 2 р – 1.

Задача 3. Доказать, что ни одно целое число вида n = 3 p (где р > 3 есть простое число) не может быть псевдопростым по основаниям 2, 5 и 7.

Задача 4. Доказать, что если число n является псевдопростым по основанию 2, то число , тоже является псевдопростым по этому же основанию.

Задача 5. Доказать, что если число n является псевдопростым по основанию b и 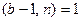, то число тоже является псевдопростым по снованию b.

Задача 6. Пусть число n имеет вид р (2 р – 1), где 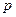и 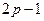– простые числа. Доказать, что n является псевдопростым Эйлера для 25% всех возможных оснований 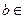Z .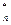

Задача 7. Доказать, что если число n является псевдопростым по основанию 2, то число является сильно псевдопростым и псевдопростым Эйлера по основанию 2.

Задача 8. Доказать, что существует бесконечное множество чисел сильно псевдопростых и псевдопростых Эйлера по основанию 2.

Задача 9. Пусть n будет числом Кармайкла 561.

(а) Определить количество оснований 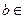Z , для которых число 561

является псевдопростым Эйлера.

(b) Определить количество оснований, по которым число 561 является сильно

псевдопростым и выписать эти основания.

Раздел седьмой

1. Задача факторизации.

Формулировка задачи выглядит так:

Задано: n >1 натуральное.

Найти: каноническое разложение числа n, т.е. представить n в виде –

разложения в произведение степеней простых чисел.

В настоящее время неизвестны эффективные алгоритмы решения этой задачи даже, несмотря на то, что она эквивалентна поиску хотя бы одного простого делителя числа n.

Лучшие из известных алгоритмов, например, метод квадратичного решета, (включая вероятностные) работают за время

,

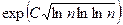при этом лучшее значение 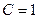. Имеется алгоритм (метод решета числовых полей) с недоказанной оценкой времени работы

.

Границей современных возможностей разложения являются числа порядка .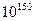

Узкая задача факторизации формулируется так:

Задано: , где р и q – различные простые.

Найти: р и q.

Для такой задачи неизвестно ничего лучшего, чем в общем случае. Некоторые алгоритмы факторизации суженной задачи могут учитывать специфические свойства чисел р и q, поэтому для использования в криптосистемах выбирают т.н. сильные простые.

Определение. Простое число р называется сильным простым, если выполняются следующие условия:

1) Число р -1 имеет большой простой делитель r;

2) Число r -1 имеет большой простой делитель;

3) Число р +1 имеет большой простой делитель.

Рассмотрим в качестве примера два алгоритма факторизации, которые применимы для разложения сравнительно небольших чисел.

1) Пробное деление.

Это самый элементарный алгоритм факторизации. При его реализации для числа 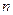пытаются, последовательно деля 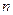на натуральные числа из диапазона 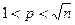, найти делитель этого числа. Учитывая, что минимальный делитель, отличный от 1, составного числа есть число простое, после нахождения такового ищут показатель кратности вхождения его в испытуемое число. В итоге получают представление вида , где 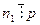. После этого ищут нетривиальный делитель в диапазоне и т. д. Ясно, что в случае, когда 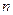есть число простое, то процедура потребует 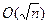шагов алгоритма, что означает, что он носит экспоненциальный характер. Но этот алгоритм вполне приемлем для разложения на множители чисел, не превосходящих .

2) (Р - 1)- метод Полларда.

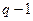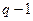Пусть число требуется разложить на множители. Будем считать, что известно такое целое число В, что является показательно В -гладким, т.е. любая степень простого числа, делящая , меньше В, а таковым не является. Тогда можно надеяться, что делит В!, в то время как , скорее всего, этого числа не делит.

Предположим, что нашли

Предположим, что можно подсчитать то же самое по модулям 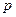и 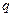, получим

,

поскольку делит В! и по малой теореме Ферма, .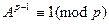

С другой стороны, равенство

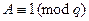
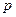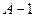маловероятно. Следовательно, делит , а 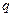этого числа не делит. Поэтому, можно восстановить 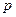, вычисляя .

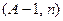На псевдокоде этот алгоритм выглядит следующим образом:

A = 2;

for (j = 2; j <= B; j++)

{ A = A^ j mod n; }

p = (A - 1, n);

if (p! = 1 && p!= n) then

вывести: «р – делитель n»;

else

вывести: «результат не получен»;

В качестве примерарассмотрим разложение числа n = 15 770 708 441. Выберем В = 180 и прогоним этот алгоритм. В результате получим

.

Применяя алгоритм Евклида, найдем

.

Отметим, что в этом примере 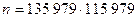. Поэтому

,

.

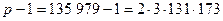Следовательно, действительно показательно 180-гладкое и даже 174-гладкое, в то время как 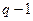таковым не является.

Можно показать, что сложность (Р – 1)-метода оценивается как

.

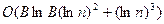Значит, выбор при некотором натуральном i обеспечивает полиномиальную сложность алгоритма, дающего, правда, результат только для чисел специального вида. Отсюда, кстати, и предпочтение сильным простым числам.

К сказанному добавим, что основным приемом в алгоритмах факторизации, который известен весьма давно, является тот, при котором генерируются два целых числа x и y приближенно той же величины, что и n, удовлетворяющих условию

.

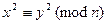Применяя формулу сокращенного умножения, получим

.

Если при этом , то вычисляя 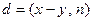можно ожидать с вероятностью ½, что будет найден нетривиальный делитель числа n. Вся сложность заключается в том, чтобы понять, как подобрать подходящие x и y.

2. Задача распознавания квадратичности.

Формулировка задачи для простого р выглядит так:

Задано: N, p – простое нечетное, .

Распознать: существует ли такое у Z, что ?

Для решения такой задачи имеются полиномиальные алгоритмы. Один из них связан с вычислением символа Лежандра 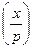, а другой опирается на критерий Эйлера для квадратичных вычетов, а именно: следует проверить выполнимость сравнения: . Алгоритмом вычисления символа Якоби и бинарным методом можно получить решение.

3. Задача извлечения корня квадратного по простому модулю.

Формулировка задачи для простого р выглядит так:

Задано: N, p – простое нечетное, .

Найти: такое у Z, что , если оно существует.

Вопрос существования, как показано выше, решается полиномиальным алгоритмом. Поэтому можно считать, что х является квадратичным вычетом. Тогда существует вероятностный алгоритм извлечения корня. Для случая, когда или 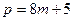соответствующий алгоритм оказывается детерминированным, а если 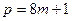, то потребуется квадратичный невычет по модулю р. Если выбрать случайный квадратичный вычет по модулю р сравнительно легко, надо лишь задать Z 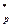и возвести его во вторую степень по модулю р, то при построении квадратичного невычета по модулю р придется воспользоваться следующей вероятностной процедурой (алгоритм типа Лас Вегас).

Вход: р – простое.

Дата добавления: 2014-11-16