
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Из последнего равенства аналогичным образом для некоторого целого неотрицательного s получаем 5 страница
|
|
|
|
1. Выбрать случайное  Z
Z 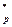 .
.
2. Применить один из указанных выше способов распознавания квадратичного вычета по модулю р. Если ответ положителен, т.е. х – квадратичный невычет, то подать его на выход, иначе, вернуться к п. 1. и повторить выбор.
Следует заметить, что так как квадратичных вычетов и невычетов по модулю р существует по  , то вероятность неудачи при каждом выборе равна ½. Поэтому при независимых выборах в серии из k опытов вероятность неудачи составит всего
, то вероятность неудачи при каждом выборе равна ½. Поэтому при независимых выборах в серии из k опытов вероятность неудачи составит всего 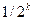 .
.
Итак, выделим три случая (предполагая, что х есть квадратичный вычет 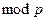 ):
):
1) если р = 4 m + 3, то по критерию Эйлера
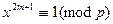
и поэтому, домножая обе части полученного сравнения на х, получаем
 ;
;
2) если р = 8 m + 5, то по критерию Эйлера
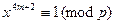 ,
,
откуда, извлекая корень квадратный из обеих частей сравнения, имеем
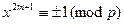 ;
;
учитывая, что в этом случае
 ,
,
получаем,
 для
для  ,
,
иначе,
 ;
;
3) если р = 8 m + 1, то здесь придется описать подробнее процедуру нахождения корня. Пусть р = 2  t + 1, где (t, 2) = 1 и k
t + 1, где (t, 2) = 1 и k  3. Из критерия Эйлера получаем, что
3. Из критерия Эйлера получаем, что
 , откуда имеем
, откуда имеем  .
.
Выберем квадратичный невычет z (mod p). Тогда
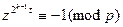 .
.
Отсюда, для любого целого s  , равного 0 или t, получаем
, равного 0 или t, получаем
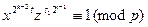 ,
,  .
.
 ,
,  .
.
Повторяя эту процедуру еще k -3 раза, получим для некоторого неотрицательного s 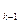 равенство
равенство
 .
.
Из него, наконец, находим
 .
.
4. Задача распознавания квадратичного вычета по модулю 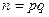 .
.
Формулировка задачи в этом случае выглядит так:
Задано: 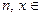 N,
N, 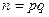 , p и q – различные простые нечетные,
, p и q – различные простые нечетные,  .
.
Распознать: существует ли такое у  Z, что
Z, что  ?
?
Решение этой задачи сводится к факторизации числа 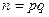 .
.
5. Задача извлечения квадратного корня по модулю 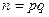 .
.
Формулировка задачи выглядит так:
Задано: 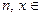 N,
N, 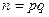 , p и q – различные простые нечетные,
, p и q – различные простые нечетные,  .
.
Найти: такое у  Z, что
Z, что  , если у существует.
, если у существует.
Ответ на вопрос этой задачи (как и обоснование ответа к предыдущей) дает теорема:
|
|
|
Теорема. Пусть 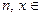 N,
N, 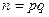 , p и q – различные простые нечетные,
, p и q – различные простые нечетные,  . Обозначим
. Обозначим 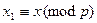 и
и 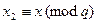 . Тогда
. Тогда
1) Если существует такое у  Z, что
Z, что
 , (7.1)
, (7.1)
то для  и
и  (7.2)
(7.2)
выполняется
 и
и  . (7.3) Справедливо и обратное: для любых
. (7.3) Справедливо и обратное: для любых 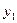 и
и  из (7.3) у из (7.2) удовлетворяет (7.1).
из (7.3) у из (7.2) удовлетворяет (7.1).
2) х является квадратичным вычетом по модулю n тогда и только тогда, когда х есть квадратичный вычет по модулю р и по модулю q.
3) Если х – квадратичный вычет по модулю n, то существует ровно четыре различных корня квадратных из х по модулю n.
В последнем пункте следует поступать так. Комбинируя пары решений по mod p и mod q, следует решать далее системы сравнений вида
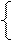 u = y
u = y  (mod p),
(mod p),
u = y  (mod q), где i, j = 1,2.
(mod q), где i, j = 1,2.
Решения этих систем дают искомые четыре варианта корня квадратного из x по mod n.
Итак, как видно из теоремы, и задача нахождения квадратного корня по модулю n сводится полиномиально к задаче факторизации. Оказывается, что существует и обратное сведение, т.е. задачу факторизации числа 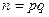 можно свести к задаче извлечения квадратного корня по модулю n.
можно свести к задаче извлечения квадратного корня по модулю n.
Теорема. Пусть 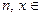 N,
N, 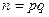 , p и q – различные простые нечетные,
, p и q – различные простые нечетные,  , а
, а 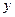 и
и 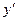 – два различных корня из х по модулю n таких, что
– два различных корня из х по модулю n таких, что  . Тогда
. Тогда  есть один из делителей р или q.
есть один из делителей р или q.
Легко представить простой Лас-Вегас оракульный алгоритм, который факторизует числа n указанного вида с доступом к оракулу  , который поставляет корень квадратный
, который поставляет корень квадратный 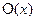 по запросу х.
по запросу х.
Вход: n = pq, где p и q – различные простые нечетные числа.
1. Выбрать случайный элемент  Z
Z 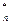 . Вычислить
. Вычислить  .
.
2. Сделать оракулу  запрос x. Пусть
запрос x. Пусть  – ответ оракула, т.е.
– ответ оракула, т.е. 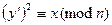 .
.
3. Если выполняется условие  , то вычислить с помощью алгоритма
, то вычислить с помощью алгоритма
Евклида  и результат подать на выход.
и результат подать на выход.
Так как y выбирается случайно, то согласно пункту 3 предыдущей теоремы условие  выполняется с вероятностью ½. Если применить алгоритм k раз, то вероятность того, что это условие не выполнится ни разу, составит
выполняется с вероятностью ½. Если применить алгоритм k раз, то вероятность того, что это условие не выполнится ни разу, составит  .
.
6. Некоторые задачи.
Задача 1. Разложить число 65621 на множители методом Полларда, приняв 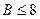 .
.
|
|
|
Задача 2. Разложить число 69799 на множители методом Полларда, приняв 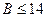 .
.
Задача 3. Разложить число 5046986363 на множители методом Полларда, приняв 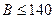 .
.
Задача 4. Извлечь корень квадратный из числа  по модулю
по модулю 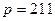 .
.
Задача 5. Извлечь корень квадратный из числа  по модулю
по модулю  .
.
Задача 6. Извлечь корень квадратный из числа 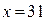 по модулю
по модулю  .
.
Задача 7. Извлечь корень квадратный из числа  по модулю
по модулю 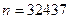 .
.
Раздел восьмой
1. Вычисление значений функции Эйлера 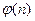 .
.
Как известно, функция Эйлера мультипликативная, поэтому по каноническому разложению числа n легко получить значение 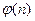 . Если же каноническое разложение числа неизвестно, то задача становится сложной. В настоящее время неизвестны эффективные алгоритмы решения задачи:
. Если же каноническое разложение числа неизвестно, то задача становится сложной. В настоящее время неизвестны эффективные алгоритмы решения задачи:
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 357; Нарушение авторских прав?; Мы поможем в написании вашей работы!