Решаем четыре системы сравнений 1 страница

u = 709 (mod 997) u = 709 (mod 997) u = -709 (mod 997) u = -709 (mod 997)

u = 276 (mod 991), u = -276 (mod 991), u = 276 (mod 991), u = -276 (mod 991).

Получаем четыре ответа: 93430, 1706, 986321, 894597 (mod 988027). Эти наборы цифр следует дополнить цифрой «0» так, чтобы длина полученного блока равнялась шести. Теперь видим, что второе число может быть преобразовано в блок «001706», который отвечает исходному начальному блоку.

Считается, что расшифрование в системе медленнее, чем шифрование, но сравнимо по скорости с расшифрованием в RSA.

5. Некоторые задачи.

Задача 1. Объяснить условие, по которому выбираемые числа 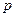и 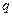в системе RSA не должны быть близки друг другу.

Задача 2. Объяснить, почему для и выбор числа 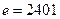в системе RSA нежелателен.

Задача 3.. Объяснить, почему для и выбор числа 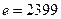в системе RSA нежелателен.

Задача 4. Объяснить, почему для 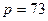и выбор числа в системе RSA нежелателен.

Задача 5. Объяснить, почему для и выбор числа в системе RSA нежелателен.

Задача 6. Сообщение на английском языке зашифровано шифром RSA:

"125272125174631912012674".

Использован следующий алфавит:

"|A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z|"

Расшифруйте сообщение, если открытый ключ , .

Задача 7. Сообщение на английском языке зашифровано шифром RSA:

"104882565235966960902355590692012154798512518317226662931550

896724287611".

Использован следующий алфавит:

"|A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z| _ |"

Расшифруйте сообщение, если открытый ключ , .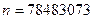

Задача 8. Сообщение на английском языке зашифровано шифром Рабина:

"2197358334310121".

Использован следующий алфавит:

"|A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z|".

Расшифруйте сообщение, если открытый ключ .

Задача 9. Сообщение на английском языке зашифровано шифром Рабина:

"011055242294483160750316501598754251285614254510".

Использован следующий алфавит:

"|A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z| _ |, |. |".

Расшифруйте сообщение, если открытый ключ .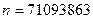

Раздел десятый

1. Вероятностная схема криптосистем с открытым ключом Голдвассера- Микели.

Идея вышеуказанной схемы состоит в том, чтобы сделать алгоритм шифрования вероятностным. Такой алгоритм ставит в соответствие открытому тексту М не один шифртекст С, а целое семейство шифртекстов . Таким образом, для каждого открытого сообщения М результат работы алгоритма Е(М) есть случайная величина, распределенная на множестве . Чтобы сделать возможным расшифрование, для любой пары различных сообщений и 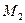соответствующие им множества шифртекстов 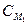и 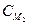не должны пересекаться. Более того, должен существовать эффективный алгоритм, позволяющий при использовании секретного ключа по любому определить М.

Такие системы считаются надежными, если для любой пары различных сообщений и 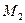одинаковой длины l случайные величины 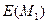и невозможно отличить одну от другой с вероятностью большей, чем никаким вероятностным полиномиальным алгоритмом. То есть с незначительной вероятностью можно определить, отвечают ли эти шифртексты одному сообщению или разным. Такой уровень надежности недоступен детерминированным системам, где разным и 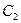всегда отвечают разные и 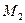. Здесь же решается и одна из проблем, связанных с тем, что некоторые открытые тексты (например, в RSA) не закрываются надлежащим образом.

Можно сказать, что вероятностные системы определенным образом по критериям стойкости приближаются к совершенным, т.е. стойким в теоретико-информационном смысле системам. Хотя, конечно, речь может идти лишь о вычислительной стойкости таких криптосистем.

2. Реализация вероятностной схемы на основе квадратичности.

Введем обозначение:

.

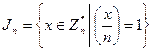Пусть n = pq, где р и q – различные простые нечетные. Если множество квадратичных вычетов по модулю n обозначить через 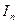, то ясно, что .Так как включение здесь строгое, то множество оказывается непустым (в нем столько же элементов, как и в 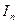). Это множество называется множеством псевдоквадратов по модулю n. Теперь рассмотрим криптосистему.

Генерирование ключей. Выбирают большие различные простые числа р и q и вычисляют их произведение n = pq. Выбирают случайный псевдоквадрат 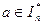и полагают: открытый ключ – n, a, а секретный ключ – р и q.

Шифрование. Открытое сообщение записывают в двоичной форме, т.е.

, где .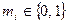

Шифртекст получают в виде , где . Правило зашифрования выглядит так:

1) Для каждого 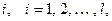независимо от остальных выбирают случайный элемент .

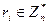2) Полагают

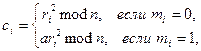
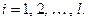
Расшифрование. По шифртексту открытый текст получают по правилу:

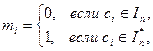
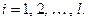
Корректность процедуры очевидна, так как если , то в шифртексте получаем квадратичный вычет по модулю n, а если , то в шифртексте получаем произведение квадратичного вычета на псевдоквадрат по модулю n, что всегда является псевдоквадратом. Значит, открытое сообщение М однозначно определяется по шифртексту С независимо от выборов случайных элементов .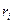

Эффективность алгоритма не подлежит сомнению, ибо все необходимые действия обслуживаются эффективными алгоритмами. Остановимся лишь на выработке случайного псевдоквадрата а. Так как простые р и q известны, то можно применить вероятностную процедуру выработки случайного квадратичного невычета по простому модулю, которая обсуждалась ранее (см. р.7). Выберем случайный квадратичный невычет 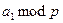и случайный квадратичный невычет , а затем остается решить систему сравнений

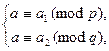
в соответствии с Китайской теоремой об остатках. Такое а, очевидно, будет случайным

псевдоквадратом по модулю n.

Стойкость системы обеспечивается сложностью задачи различения квадратичных вычетов по модулю n от псевдоквадратов по этому же модулю. Эффективные алгоритмы решения этой задачи неизвестны. Как указывалось, задача эта может быть сведена к задаче факторизации числа n, но множители р и q задаются секретным ключом. Поэтому в таком случае речь идет о поиске секретного ключа по открытому.

3. Реализация вероятностной схемы на основе RSA.

Рассмотрим кратко еще одну вероятностную схему.

Генерирование ключей. Эта процедура производится так же, как и в самой RSA.

Открытый ключ: е, n, где n = pq, .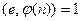

Секретный ключ: d такое, что .

Шифрование. Открытое сообщение записывают в двоичной форме, т.е.

, где ,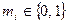

и преобразуют в шифртекст , где 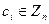, для каждого производя следующие вероятностные процедуры:

1) если , то в 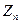выбирают случайное четное число 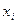, а если , то выбирают случайное нечетное число ;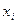

2) вычисляют .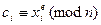

Расшифрование. По шифртексту открытый текст получают по правилу:

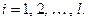
Доказано, что надежность рассматриваемой системы равносильна допущению, что RSA может быть вскрыта полиномиальным алгоритмом.

4. Криптосистема ЭльГамала.

Эта вероятностная блочная система была предложена ЭльГамалом в 1985 г.

Генерирование ключей. Выбирают большое простое число р и целое число 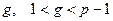, которое в мультипликативной группе Z 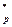имеет большой порядок. В идеальном случае g является первообразным корнем по модулю р. Эти два числа не составляют тайны и находятся в общем пользовании абонентов информационной сети. Каждый абонент выбирает целое число и вычисляет . Полагают:

Открытый ключ: .

Секретный ключ: а.

Шифрование. Каждый блок открытого текста М представляют элементом множества Z 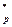. Сообщение 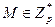преобразуют в шифртекст 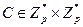следующим образом:

1) Выбирают случайное целое число .

2) Вычисляют , где

Расшифрование. Имея секретный ключ и шифртекст , вычисляют

.

Корректность процедуры легко проверяется. Для любого выбранного r всегда из имеющегося шифртекста С, полученного в результате шифрования, однозначно восстанавливается открытое сообщение М.

Эффективность алгоритма обеспечивается бинарным методом и расширенным алгоритмом Евклида. Имеется трудность построения первообразных корней по модулю р. Поэтому следует пользоваться построением пары р и g, как описывалось в р.8.

Вопрос о стойкости можно представить следующей задачей раскрытия системы.

Задано: где

для некоторых .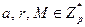

Вычислить: М.

Эта задача эквивалентна следующей задаче:

Задано: где

для некоторых .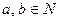

Вычислить: .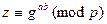

Ясно, что вторая задача сводится к дискретному логарифмированию по модулю р. Поэтому следует при генерировании ключей исключить те варианты, при которых возможно эффективное дискретное логарифмирование. В частности, надо выбирать простое число р таким, чтобы число р - 1 содержало бы большой простой делитель. Такой выбор препятствует быстрой факторизации р - 1 и не позволяет воспользоваться алгоритмом Силвера-Полига-Хеллмана. В настоящее время доказано, что если 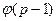имеет лишь малые простые делители, то задача раскрытия системы ЭльГамала эквивалентна дискретному логарифмированию.

Приведем пример шифрования по системе ЭльГамала. Пусть задан открытый текст:

«TIMEO DANAOS ET DONA FERENTES».

Его цифровой эквивалент, разбитый на блоки длины шесть, выглядит так (здесь вновь

добавляется в конце текста буква «J»):

«190812 041426 030013 001418 260419 260314 130026 050417 041319 041809».

Пусть выбрано простое р = 994991. В качестве числа g выберем первообразный корень по mod p: g = 7. Далее, выбираем число а = 475 и вычисляем h = 659454 (mod 994991).

Возьмем r = 211 общим на все блоки открытого текста. Тогда с = 073747. Цифра «0»

в начале приписана для того, чтобы с имел вид блока длины шесть. Вычисляя по описанному выше правилу элементы вида с и собирая их вместе, получаем шифртекст, где в начале записано с , служащее своеобразной подсказкой при расшифровке:

«073747 127613 201338 222776 758335 502424 595730 925985 939171 182708 742271».

Расшифруем второй блок полученного выше шифртекста.

.

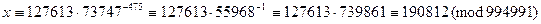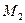Как видим, получился первый блок цифрового представления открытого текста. В этом примере одна величина с вычислена для всех блоков текста из соображений простоты демонстрации примера. На самом деле для каждого блока выбирается случайным образом свое r и вычисляется свое с . Действительно, если для разных и величина r общая, то , и 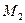может быть вычислено, если известно.

На сегодняшний день (2013 г.) критический размер p более 1300 бит. Но p может выбираться до 4096 бит.

5. Некоторые задачи.

Задача 1. Сообщение на русском языке зашифровано шифром на основе

квадратичности.

Использован следующий алфавит:

"|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|_|"

Криптограмма:

04489 04555 02695 03202 06566

00480 01163 03811 03978 05287

06782 03670 00485 01408 00772

02267 02572 05797 01474 03196

04324 05026 01250 06875 05221

02630 01353 00893 00419 03836

Расшифровать текст, если открытый ключ .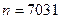

Задача 2. Сообщение на русском языке зашифровано шифром на основе

квадратичности.

Использован следующий алфавит:

"|а|б|в|г|д|е|ж|з|и|й|к|л|м|н|о|п|р|с|т|у|ф|х|ц|ч|ш|щ|ъ|ы|ь|э|ю|я|_|"

Криптограмма:

02209 02968 04159 00899 03407

02790 05392 00342 02199 05775

00477 05589 02209 01510 00709

01852 01603 01380 03728 00540

00058 01753 04684 01521 03998

05630 03632 01334 00976 04353

Расшифровать текст, если открытый ключ .

Задача 3. Текст на русском языке зашифрован вероятностной системой на основе RSA

в алфавите без пробела и буквы «ё». Криптограмма:

242 360 292 231 137

100 151 128 248 102

227 015 227 169 032

082 241 305 109 125

136 113 267 245 087.

Расшифровать текст, если известен открытый ключ , .

Задача 4. Текст на русском языке зашифрован вероятностной системой на основе RSA

в алфавите без пробела и буквы «ё». Криптограмма:

180 116 058 125 043 156

068 072 127 034 049 040

011 074 064 165 020 044

092 161 101 185 109 018

047 126 023 179 036 088.

Расшифровать текст, если известен открытый ключ , .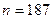

Задача 5. Сообщение на английском языке зашифровано шифром ЭльГамала:

"22*7992085239888300224888".

Использован следующий алфавит:

"|A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z|".

Расшифруйте сообщение, если

открытый ключ ,

открытый ключ ,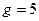

открытый ключ , и величина С1 – выбрана общей для всех блоков

и равна 22.

Задача 6. Сообщение на английском языке зашифровано шифром ЭльГамала:

«2806707020355362843694880343848866345868223530330923035323001642

31212610035549906852953213146186».

Использован следующий алфавит:

«|A|B|C|D|E|F|G|H| I | J |K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z| _ |, |. |».

Расшифруйте сообщение, если

открытый ключ ,

открытый ключ ,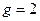

открытый ключ 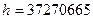, и величина С1 – выбрана общей для всех

блоков.

Раздел одиннадцатый

1. Эллиптические кривые. Группа точек кривой.

Криптографические приложения теории эллиптических кривых – очень молодой раздел в криптографии. Его появление диктуется необходимостью поиска задач такой вычислительной сложности, которая бы гарантированно обеспечивала стойкость криптографических объектов. N. Koblitz был одним из авторов идеи применения эллиптических кривых в данной области. Главным здесь явилось использование группы точек кривой в том же качестве, в котором теоретико-групповые объекты присутствуют в двухключевой криптографии. Эта группа, вообще говоря, не является циклической. От- сюда возникают надежды на усложнение вычислительных задач, связанных с такой группой.

Обозначим через К некоторое поле. Нас будут интересовать прежде всего поля: R вещественных чисел, Q – рациональных чисел и F , имеющее 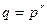элементов.

Определение. Пусть К будет полем характеристики 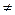2, 3 и пусть 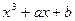, где

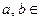К, многочлен третьей степени, не имеющий кратных корней. Тогда э ллиптической кривой над полем К называется множество точек (x, y), где К, удовлетворяющих уравнению

, (11.1)

вместе с элементом, обозначаемым через О и называемым «бесконечно удаленной точкой» (о котором будет сказано далее).

Эллиптические кривые определяются над различными полями. В частности, если характеристика поля равна 2 или равна 3, то уравнение (11.1) выглядит иначе. Покажем свойства точек эллиптической кривой, множество которых образует абелеву группу и для наглядности будем считать, что К = R, т.е. эллиптическая кривая есть обычная кривая на плоскости (вместе с “точкой О в бесконечности”).

Определение. Пусть Е будет эллиптической кривой над полем вещественных чисел, и P и Q будут точками этой кривой. Определим точку противоположную Р и сумму Р + Q следующим образом:

1) Если Р есть точка в бесконечности О, то определим – Р = О и Р + Q = Q; далее, точка О служит нейтральным элементом (или нулем) группы точек. В дальнейшем полагаем, что ни Р, ни Q не являются точками в бесконечности.

2) Противоположный элемент – Р есть точка с той же координатой х, что и Р, однако с противоположной координатой y, т.е. – (x, y) = (x, - y). Из уравнения (11.1) с очевидностью вытекает, что если точка (x, y) лежит на кривой, то и точка (x, - y) также лежит на этой кривой.

3) Если точки Р и Q имеют различные координаты х, то нетрудно заметить, что прямая l = 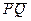пересекает кривую еще точно в oдной точке R (разве только эта прямая является касательной к кривой в точке Р и тогда берем R = P или является касательной в точке Q и тогда берем R = Q). В качестве суммы Р + Q берем точку –R, т.е. точку симметричную (относительно оси х) к той третьей точке пересечения. Геометрическая конструкция точки P + Q показана на рисунке ниже.

4) Если Q = - P (т.е. точка Q имеет ту же координату х и противоположную координату у), то определим P + Q = O (точка в бесконечности). (См. условие (2))

5) Остается последняя возможность Р = Q. Пусть прямая l будет касательной к кривой в точке Р, и пусть R будет единственной точкой пересечения прямой l с кривой, отличной от Р. Тогда определим Р + Q = - R. (Если прямая l является «двойной касательной» к

кривой, т.е. точка Р является точкой перегиба кривой, то в качестве R берем саму точку Р.)

Пример. Эллиптическая кривая, отвечающая уравнению на плоскости, представлена на рисунке справа. На нем изображен типовой случай сложения двух

точек Р и Q. Рисуем секущую, проходящую

через 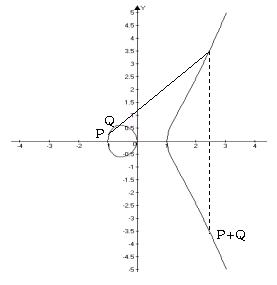точки Р и Q и в качестве Р + Q берем

точку, симметричную (относительно оси х)

к третьей точке пересечения прямой, прохо-

дящей через Р и Q с кривой. Если точки Р и

Q совпадают, т.е. когда ищется точка 2Р, ри-

суем прямую, касательную к кривой, в точке

Р; тогда точкой 2Р является точка, симмет-

Дата добавления: 2014-11-16