Решаем четыре системы сравнений 7 страница

1.

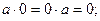
2.

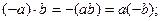
3. 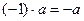(для кольца с единицей);

4. 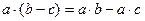, где ;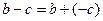

5.

Определение 2. Два ненулевых элемента кольца, произведение которых равно нулю, называются делителями нуля кольца.

Пример 9. Кольцо из примера 2 имеет делители нуля в случае, когда 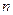– составное число; кольцо из примера 5 имеет делители нуля при 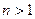, а кольцо из примера 7 имеет делители нуля без дополнительных оговорок. Кольца из примеров 1, 4, 6 и 8 не имеют делителей нуля.

Если кольцо не имеет делителей нуля, то в нем справедливы т.н. законы сокращения:

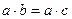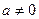6. Если и , то ;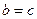

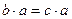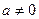7. Если и , то .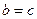

Определение 3. Коммутативное кольцо с единицей 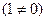и без делителей нуля называется областью целостности, или целостным кольцом.

Определение 17. Целостное кольцо, в котором каждый ненулевой элемент обратим, называется

полем.

Пример 10. 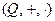– поле рациональных чисел.

Пример 11. 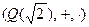– вещественное «квадратичное» поле.

Пример 12. 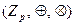, р – простое число. Это поле классов вычетов по простому модулю р.

Пример 13. 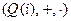– поле гауссовых чисел.

Конечно, полями являются и множества вещественных и комплексных чисел относительно стандартных операций сложения и умножения, заданных в них.

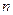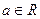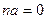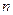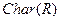Определение 4. Пусть – произвольное кольцо. Если существует такое натуральное , что для любого выполнено , то наименьшее с таким свойством называется характеристикой кольца и обозначается . В противном случае говорят, что кольцо имеет нулевую характеристику.

Лемма 1. Если кольцо с единицей 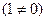и без делителей нуля имеет положительную

характеристику, то эта характеристика есть простое число.

Следствие. Положительная характеристика поля есть простое число. В частности, характеристика конечного поля есть простое число

Пример 14. Поле из примера 12 имеет характеристику, равную р.

Теорема1. Пусть – коммутативное кольцо простой характеристики р. Тогда

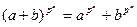и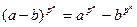

для всех 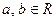и .

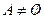Определение 5. Пусть – кольцо. и 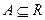. 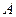называют подкольцом кольца , если 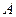является кольцом относительно сужения операций, определенных в кольце .

Пример 15. Четные числа образуют подкольцо в кольце всех целых чисел.

Пример 16. Диагональные матрицы образуют подкольцо в кольце квадратных матриц.

Теорема2. Непустое подмножество 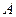кольца является подкольцом в нем тогда и только тогда, когда выполнены условия:

1) ;

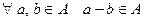2) .

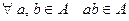Заметим, что подкольцо наследует не все свойства родительского кольца. Это хорошо видно на примерах 1 и 6.

Определение 6. Подкольцо кольца называется (двусторонним) идеалом в кольце , если

.

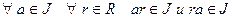Пример 17. Подкольцо четных чисел есть идеал в кольце всех целых чисел. По аналогии, числа кратные некоторому 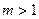также образуют идеал в этом кольце.

Пример 18. Пусть R – коммутативное кольцо и 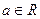. Тогда 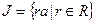есть идеал в R.

Пример 19. Пусть R – коммутативное кольцо и 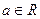. Тогда множество 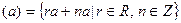есть наименьший идеал в R, содержащий элемент .

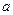Пример 20. Пусть R – коммутативное кольцо с единицей и 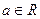. Тогда множество .

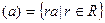Определение 7. Пусть R – коммутативное кольцо. Идеал кольца R называется главным, если существует элемент 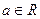такой, что 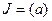. В этом случае называют идеалом,

порожденным элементом .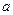

Идеалы, очевидно, являются нормальными подгруппами в аддитивной группе кольца. Поэтому смежные классы по идеалу образуют аддитивную группу. Эти классы еще называют классами вычетов по идеалу . Принадлежность одному классу двух элементов называют сравнимостью по модулю идеала. Таким образом, 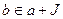тогда и только тогда, когда 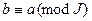. Легко проверяются следующие свойства такой сравнимости:

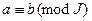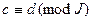1) Если и , то ;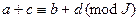

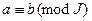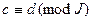2) Если и , то ;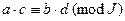

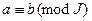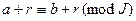3) Если , то для любого ;

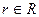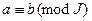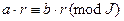4) Если , то и 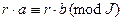для любого ;

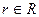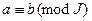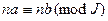5) Если , то для любого .

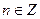Учитывая эти свойства нетрудно непосредственно показать, что следующие операции над классами корректны:

;

.

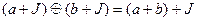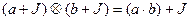Лемма 2. Фактормножество 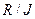относительно описанных выше операций над классами образует кольцо, которое называется факторкольцом кольца по идеалу .

Пример 21. Нетрудно усмотреть, что факторкольцо 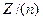есть ни что иное, как кольцо классов вычетов по модулю 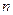, т.е. .

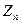Теорема 3. Факторкольцо 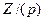кольца 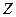целых чисел по главному идеалу, порожденному простым числом 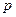, является полем.

Дадим еще несколько определений. Пусть – коммутативное кольцо с единицей.

Определение 8. Элемент 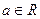называется делителем элемента 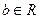, если существует элемент

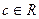такой, что .

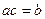Определение 9. Делители единицы называются обратимыми элементами кольца.

Определение 10. Элементы a и b из называются ассоциированными, если существует обратимый элемент 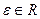такой, что .

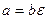Определение 11. Элемент 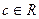называется простым элементом кольца , если он не является обратимым элементом и не имеет других делителей, кроме ассоциированных с ним элементов или обратимых элементов.

Определение 12. Идеал 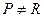кольца называется простым идеалом, если для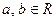

включение 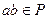имеет место лишь в том случае, когда либо 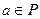, либо .

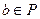Определение 13. Идеал 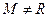кольца называется максимальным идеалом, если для любого идеала кольца включение 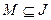влечет за собо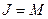й или .

Определение 14. Целостное кольцо называется кольцом главных идеалов, если каждый идеал кольца является главным, т.е. существует элемент 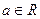такой, что

.

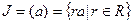Теорема 4. Пусть – коммутативное кольцо с единицей. Тогда

(i) Идеал M кольца R является максимальным тогда и только тогда, когда факторкольцо

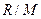является полем.

(ii) Идеал P кольца R является простым тогда и только тогда, когда факторкольцо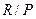

является целостным кольцом.

(iii) Каждый максимальный идеал кольца R является простым.

(iv) Если – кольцо главных идеалов, то факторкольцо 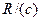является полем в том и только в том случае, когда c – простой элемент кольца .

Пример 22. – кольцо главных идеалов. Это легко показать, используя теорему о делении с остатком. В этом кольце роль простых элементов играют простые числа, правда, «со знаком». Отсюда получается еще одно доказательство, что кольцо классов вычетов по простому модулю есть поле.

Пример 23. 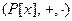– кольцо многочленов над полем P от буквы х есть также кольцо главных идеалов. Простыми элементами здесь выступают неприводимые многочлены над полем P. Поэтому факторкольцо 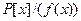, где f(x) – неприводим над P, есть поле.

Пример 24. Покажите, что – кольцо целых гауссовых чисел есть кольцо главных идеалов. Укажите простые элементы в этом кольце.

Пример 25. Опишите факторкольцо .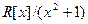

Пример 26. Опишите и сравните факторкольца 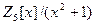и 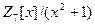. Постройте таблицы Кэли операций над классами в этих кольцах.

Определение 15. Пусть – поле и 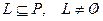. Тогда называется подполем в , если само является полем относительно сужения операций, определенных в . При этом поле называется расширением поля .

Определение 16. Поле называется простым, если не имеет собственных (т.е. отличных от него самого) подполей.

Пример 27. Поле рациональных чисел есть простое поле. Оно является подполем любого числового поля.

Пример 28. 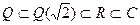. Цепочка включений для числовых полей, называемая башней полей. Но 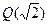не является подполем в 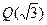и наоборот!

Пример 29. Поле является простым. Проверьте это.

Раздел девятнадцатый

Расширения полей. Простое расширение. Конечное расширение. Алгебраичность.

Определение 17. Пусть 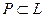– башня полей и . Тогда 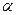называется алгебраическим элементом над полем , если существует многочлен 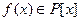, , 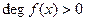такой, что 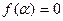. Если такого многочлена не существует, то 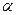называется трансцендентным элементом над полем .

Пример 1. 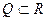, 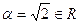. Тогда 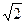алгебраичен над полем , ибо является корнем многочлена .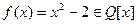

Пример 2. 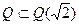, 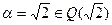. И здесь 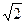алгебраичен над полем .

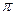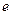Пример 3. Можно показать, что вещественные числа и трансцендентны над полем .

Надо отметить, что понятия алгебраичности и трансцендентности относительны, т.е. прямо связаны с полем, над которым рассматриваются.

Определение 18. Пусть 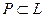– башня полей. Расширение поля называется алгебраическим, если каждый элемент алгебраичен над . В противном случае называется трансцендентным расширением поля .

Определение 19. Пусть 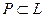– башня полей, – алгебраический над полем элемент. Тогда нормированный многочлен наименьшей степени из кольца 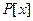, корнем которого является 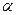, называется минимальным многочленом элемента 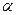над .

Лемма 1. Минимальный многочлен алгебраического элемента 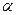над полем неприводим над .

Этим свойством и условием нормированности многочлен определен однозначно.

Определение 20. Пусть 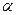есть алгебраический над полем элемент. Тогда степень его

минимального многочлена называется степенью элемента 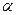над полем .

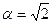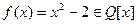Пример 4. Легко видеть, что минимальным многочленом элемента над полем есть многочлен . И тогда степень 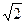над равна 2.

Пример 5. Минимальным многочленом числа 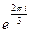над полем является многочлен 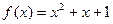. И, значит, степень и этого элемента над полем тоже равна 2.

Пример 6. Любой корень многочлена 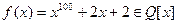имеет степень 100 над полем , ибо указанный многочлен неприводим над этим полем (по признаку Эйзенштейна) и, значит, является минимальным для своих корней (например, из поля 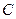) над полем рациональных чисел.

Лемма 2. Пусть – поле и 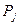– подполя поля , 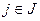. Тогда пересечение 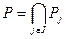есть подполе поля .

Следствие. Пересечение всех подполей данного поля является простым полем. Это поле называют простым подполем этого поля.

Определение 21. Пусть задана башня поле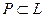й и 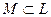. Тогда наименьшее по включению подполе в , содержащее одновременно поле и множество 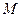называется

расширением поля , полученным присоединением к нему множества 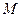и обозначается .

Легко понять, что есть пересечение всех подполей в , содержащих и 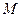. Если множество 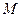является конечным, например, 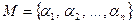, то пишут .

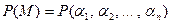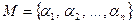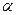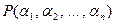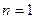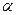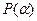Определение 22. Если и каждый присоединяемый элемент алгебраичен над полем , то расширение называется алгебраически порожденным. При этом, если , то расширение называется простым алгебраическим (а если трансцендентно над , то называется простым трансцендентным расширением).

Дата добавления: 2014-11-16