Среднее арифметическое значение, средняя квадратичная и средняя арифметическая погрешности измеряемой величины

Первой величиной, которую приходится вычислять при обработке результатов опытов, является среднее арифметическое из результатов ряда измерений, которое определяется по формуле (6).

Практически число измерений всегда ограничено, поэтому среднее арифметическое 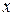не равно истинному значению измеряемой величины 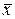, но будет тем ближе к нему, чем больше число выполненных измерений 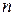. В теории вероятностей доказывается, что среднее арифметическое из результатов отдель­ных измерений является наиболее вероятным значением измеряемой величины. Это утверждение справедливо при условии, когда все измерения равноточные, а распределение погрешности измерений подчиняется вышеупомянутому закону распределения— закону Гаусса.

Если вместо истинного значения неизвестной величины использовать среднее арифметическое 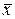, тогда на основании равенства (1) имеем:

(11)

В (11) погрешность 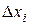несколько отличается от истинной и называется абсолютной погрешностью единичного измерения

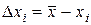(12)

Лучшим из критериев для оценки погрешностей результатов измерений является средняя квадратичная погрешность, которая характеризует степень (меру) рассеяния результатов отдельных измеренийоколо среднего их значения. Для определения среднеквадратической погрешности единичных изме­рений при ограниченном числе опытов используется формула (7), которая с учетом (12) записывается в виде:

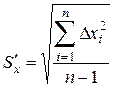. (13)

Средняя квадратическая погрешность, вычисляемая по формуле (13), характеризует погрешность единичного результата из всего ряда n измерений.

Как уже отмечалось, при увеличении числа n измерений наблюдается взаимная компенсация случайных ошибок. Поэтому усредненная средняя квадратичная погрешность 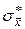, определяемая по формуле (9) и характеризующая окончательный результат измерений, уменьшается при увеличении числа n повторных измерений искомой величины. Поскольку вычисления величины достаточно громоздки, то в ряде случаев (если не оговорено в условиях решаемой задачи) для оценки ошибки, допущенной при определении средней величины, пользуются средней арифметической погрешностью, которая вычисляется как средняя величина всех величин абсолютных погрешностей единичных измерений (12), взятых по модулю:

. (14)

Так как суммирование в (14) выполняется без учета знака 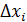, то формула (14) даёт среднее значение максимальной возможной погрешности.

Вопрос о том, какой формулой пользоваться при оценке измерений, решается при планировании эксперимента. Считается, что при числе измерений меньше пяти можно ограничиться вычислением средней абсолютной погрешности по формуле (14).

Средняя абсолютная погрешность даёт возможность указать пределы (интервал), внутри которых заключено истинное значение измеряемой величины.

Сама по себе абсолютная погрешность не даёт достаточно наглядного представления о степени точности измерения, поэтому для оценки точности результата применяется относительная погрешность. Относительная погрешность величины x при ограниченном числе опытов вычисляется по формуле:

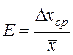. (15)

Дата добавления: 2014-11-08