Умови збіжності ітераційного процесу

Описаний вище алгоритм дозволяє отримати розв’язок системи (3.2) близький до точного (з заданою похибкою 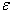) тільки в тому випадку, коли ітераційний процес пошуку розв’язку СЛАР збігається.

Теорема про збіжність. Ітераційний процес пошуку розв’язку системи лінійних алгебраїчних рівнянь виду (3.5) наближеними методами збігається, якщо будь-яка канонічна норма матриці .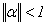

Канонічною нормою матриці називається будь-яке дійсне додатне число, яке визначається за такими умовами:

перша канонічна норма – це максимальна з сум модулів елементів матриці коефіцієнтів 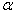пострічкам:

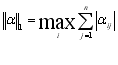, (3.9)

друга канонічна норма – це максимальна з сум модулів елементів матриці коефіцієнтів 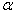постовбцям:

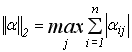, (3.10)

третя канонічна норма – це корінь квадратний з сум квадратів модулів всіх елементів матриці коефіцієнтів :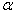

.

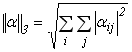Наслідок 1: Ітераційний процес розв’язання системи (3.4) збігається, якщо сума модулів елементів стрічок матриці коефіцієнтів 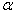або сума модулів елементів її стовбців менш одиниці, тобто виконується умова

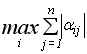<1 або умова 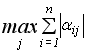<1. (3.11)

Наслідок 2: Ітераційний процес розв’язання системи (3.4) збігається, якщо елементи головної діагоналі більше суми модулів елементів відповідної стрічки крім діагонального елементу цієї стрічки, тобто виконується умова:

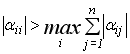або умова 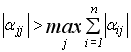. (3.12)

Приклад.

Визначити, чи збігається ітераційний процес для системи рівнянь

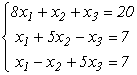або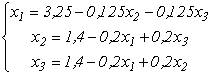

Матриця 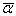даної системи має вигляд:

Визначаємо норми:

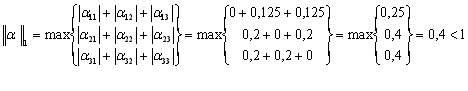
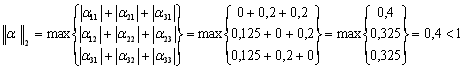
Таким чином, перша та друга канонічні норми менш одиниці, тобто ітераційний процес для даної системи збігається.

Розглянемо особливості алгоритмів наближених методів.

3.4 Метод послідовних наближень (метод Якобі)

Нехай задана система лінійних алгебраїчних рівнянь виду (3.2). Метод послідовних наближень (метод Якобі) відноситься до ітераційних методів, тому потребує перетворити дану систему до нормального вигляду (3.5) та знайти канонічні норми матриці 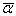, для того щоб визначити умови збіжності ітераційного процесу (3.9) - (3.11) пошуку розв’язку системи с заданою похибкою 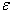відповідно теоремі про збіжність. Якщо жодна з умов (3.3) – (3.11) не виконується, то дану систему необхідно перетворити по певним правилам, та знову перевірити умови збіжності ітераційного процесу (3.9) – (3.11). Якщо жодна з умов знову не виконується, то метод послідовних наближень не має сенсу використовувати. Якщо хоча б одна з умов (3.9) – (3.11) виконується, то ітераційний процес пошуку розв’язку системи с заданою похибкою 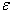збігається і метод послідовних наближень можна використовувати.

По-перше, вибирається певне значення вектору початкових наближень , яке підставляється в праву частину системи рівнянь виду:

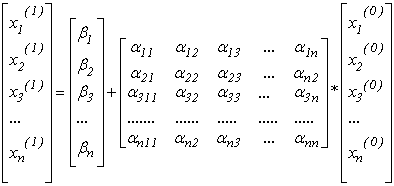, (3.13)

що легко розв’язується для знаходження вектора розв’язку першого наближення 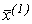, тому що в правої частині містить всі визначені елементи.

По-друге, перевіряється виконання умови закінчення ітераційного процесу виду:

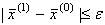
де 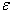- задана похибка результатів розв’язання задачі. Якщо умова не виконується, то 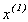підставляється в праву частину системи (3.5) і знаходиться :

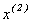та знову перевіряється виконання умови закінчення ітераційного процесу виду:

.

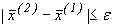За аналогією будь-яке (К+1)-е наближення можна обчислити за формулою:

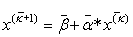, де к=0,1,2..... (3.14)

Якщо послідовність 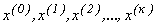, що отримана в результаті ітераційного процесу, має границю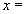 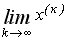, то ця границя є розв’язком системи. Умова закінчення ітераційного процесу має вигляд:

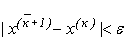, (3.15)

де 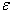- задана похибка результатів розв’язання системи.

Алгоритмічно перевірка умови (3.15) представляє собою алгоритм пошуку максимального відхилення між координатами вектора 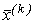і 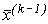і порівняння його з заданою похибкою .

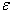Алгоритм методу послідовних наближень зображено на рисунку 3.1

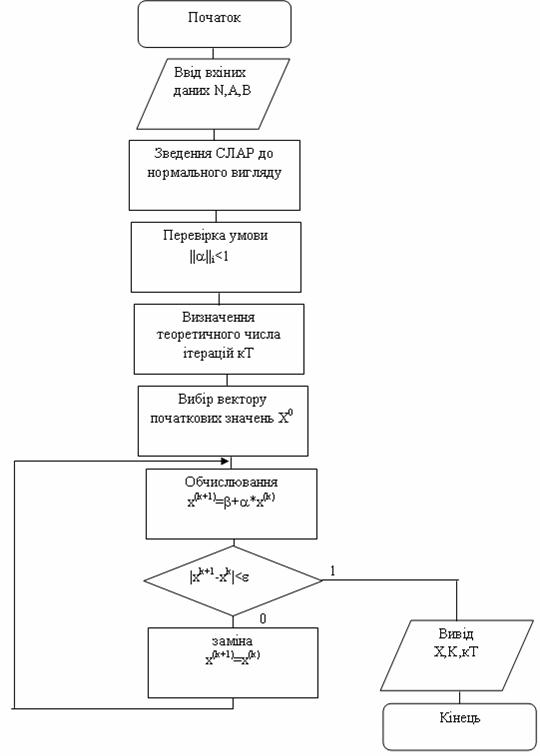
Рисунок 3.1. – Схема алгоритму методу послідовних наближень

Оцінка похибки метода Якобі

Якщо задана допустима похибка обчислень 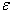і x - вектор точного розв’язку системи лінійних рівнянь, а 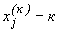-те наближення до вектору точного розв’язку, то для оцінки похибки метода послідовних наближень використовується формула:

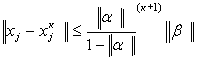, (3.16)

де 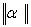- одна з 3 норм матриці 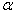; - аналогічна норма вектора 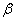; - кількість ітерацій, необхідна для досягнення потрібної точності .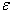

Дата добавления: 2014-11-08