Гіперболічні рівняння

Знайомство з даним типом диференційних рівнянь у частинних похідних почнемо з розгляду відповідної фізичної задачі.

Припустимо, що струна довжиною L, натягнута між двома точками осі х, точкою х = 0 і точкою x = L. Натяг струни дорівнює Т. Якщо відхилити струну від положення рівноваги і відпустити, то вона почне коливатися. Зсув кожної точки струни щодо положення рівноваги залежить не тільки від координати х цієї точки, але і від часу t. Відхилення струни від положення рівноваги описується рівнянням гіперболічного типу, що наводиться без виведення

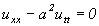
для і t>0. Коефіцієнт а враховує фізичні характеристики Тут? – вага струни на одиницю довжини, Т – натяг, g – прискорення сили ваги. Це рівняння звичайне називається хвильовим рівнянням. Для простоти а = 1, так що задача виразиться в такий вид:

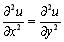(11.17)

(11.18)

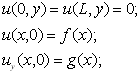
(11.19)

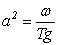
Таке формулювання задачі зовсім не означає втрати спільності, тому що проста заміна змінних зводить будь-яке хвильове рівняння до виду (11.17).

Оскільки кінці струни закріплені, то

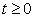, (11.20)

початковими умовами є початковий зсув

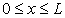, (11.21)

та початкова швидкість

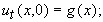
(11.22)

Наприклад, якщо відтягнути струну за середину, як показано на рис. 11.6 і відпустимо її без додавання їй початкової швидкості, то початкові умови запишуться у вигляді

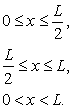
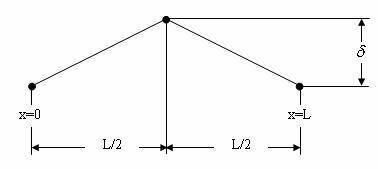
Рис. 11.6 – Можливі початкові умови для коливальної струни, описуваної хвильовим рівнянням.

Помітимо, що ці умови називаються початковими, а не граничними. У дійсності, якщо задати для гіперболічного рівняння граничні умови, то отримана задача не буде мати єдиного розв’язку. Подібні задачі називаються некоректно поставленими. Дуже важливо, щоб додаткові умови належним чином відповідали кожному типу рівнянь.

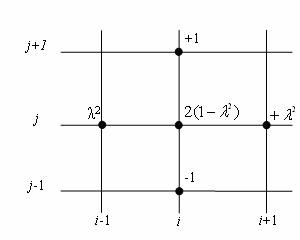
Рисунок 11.7 – Різницева схема для гіперболічного рівняння

Щоб знайти різницеві рівняння, що відповідають (11.17),, скористаємося знову рівностями (11.18) і (11.19), причому замість у записується t. Знову накреслюючи сітку, але тепер ця сітка простирається нескінченно в напрямку позитивних значень t. Можна шукати роз’язок для як завгодно далекого моменту часу. У напрямку х приймаємо крок сітки рівним h, у напрямку t – рівним k. Тому інтервал L розділяється на п = L/h малих інтервалів h, а в напрямку t може бути як завгодно багато інтервалів k.

Якщо позначити

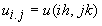і ,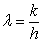

то різницеве рівняння запишеться у вигляді

(11.23)

для i = 1, 2,..., п і для j = 1, 2,....

Різницева схема при цьому виглядає так(рис.11.7):

Граничну умову (11.20) легко записати у вигляді

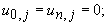j = 1,2,3,... (11.24)

Початкову умову (11.21) можна написати у вигляді

i=1,2,..,n-1... (11.25)

Щоб записати в різницевому вигляді початкову умову (11.22), можна використовувати рівність (11.3), тоді отримаємо:

.

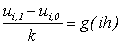Після цього, використовуючи (11.25), одержуємо

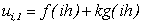(11.26)

Помітимо тепер, що (11.25) і (11.26) дають значення 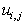для перших двох рядків: (j = 0 і j = 1). Підставляючи j = 1 у (11.23), одержимо

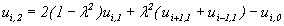(11.27)

Усі доданки в правій частині цього рівняння включають значення і тільки з перших двох рядків сітки; всі ці значення відомі з початкових умов. Тому в останньому рівнянні є тільки одне невідоме і всі значення функції, що відповідають третьому рядку, можна обчислити в явному вигляді. Після цього можна обчислювати значення функції в четвертому рядку, виходячи зі значень у другому і в третьому рядках, і т.д. стільки разів, скільки буде потрібно. При цьому навіть не приходиться вирішувати систему рівнянь.

Таким чином, (11.27) являє собою явну схему рішення хвильового рівняння. Схема алгоритму представлена на рис. 11.8.

Рисунок 11.8 – Схема алгоритму розв'язування гіперболічного рівняння на ЕОМ

При роз’язанні еліптичного рівняння (11.13) було використано схему, в якої в кожному рівнянні було більш ніж по одному невідомому; таким чином, цей метод можна було назвати неявним.

Розглянемо тепер питання збіжності і стійкості методу (не приводячи доведень, а обмежуючись тільки аналізом остаточних результатів). Можна стверджувати, що рішення (11.27) сходиться (мається на увазі, що при h?0 і k?0 розв’язання різницевого рівняння асимптотично наближається до розв‘язання диференціального рівняння), якщо

чи, що те ж саме, k<h< i=""></h<>

Ця умова є достатньою для збіжності; але вона не є необхідною. Іншими словами, існують рівняння і величини інтервалів, при яких ця умова не виконується, але усе-таки виходить вірний результат. Уся справа в тім, що тоді не можна гарантувати збіжність чисельного розв‘язку.

Таким чином, як тільки обрана величина інтервалу розбивки h у напрямку х, то з'являється обмеження на величину інтервалу по t. Якщо необхідно зробити обчислення для великого відрізка t, то може знадобитися велика кількість кроків.

Іншою настільки ж важливою обставиною є те, що при 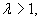метод стає нестійким, як в абсолютному, так і у відносному змісті. Це означає, як і для звичайних диференційних рівнянь, що будь-які помилки зростають у ході обчислення розв’язку.

Дата добавления: 2014-11-08